《高等数学》课程教学资源（PPT课件）Ⅱ_第九章 第六节 多元函数微分学的几何应用

第之节 第八章 多无面数微分学的儿何应用 空间曲线的切线与法平面 二、 曲面的切平面与法线

第六节 复习 目录 上页 下页 返回 结束 一、空间曲线的切线与法平面 二、曲面的切平面与法线 多元函数微分学的几何应用 第八章

复习：平面曲线的切线与法线 已知平面光滑曲线y=f(x)在点(xo,yo)有 切线方程y-y0=f'(xox-x0) 法线方程y-y0=- f(xo) x-o) 若平面光滑曲线方程为F(x,y)=0,因 dyE(x,y) dx Fy(x,y) 故在点(x0,y0)有 切线方程F(xo,0)(x-xo)+F,(x0,%Xy-0)=0 法线方程F(x0,%x-x0)-F,(xo,o)(y-%)=0 -m 下页返回

复习: 平面曲线的切线与法线 已知平面光滑曲线 ( , ) 0 0 x y 切线方程 0 y − y 法线方程 0 y − y 若平面光滑曲线方程为 ( , ) ( , ) d d F x y F x y x y y x = − 故在点 切线方程 法线方程 ( ) 0 ( , )( ) + Fy (x0 , y0 ) y − y 0 0 0 F x y x x x − = 0 ( )( ) 0 0 = f  x x − x ( ) ( ) 1 0 0 x x f x −  = − 在点 有 有 因 ( , )( ) 0 Fy (x0 , y0 )(x − x0 )− Fx x0 y0 y − y0 = 机动 目录 上页 下页 返回 结束

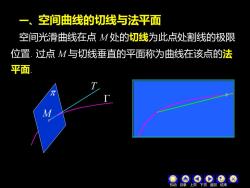
一、空间曲线的切线与法平面 空间光滑曲线在点M处的切线为此点处割线的极限 位置.过点M与切线垂直的平面称为曲线在该点的法 平面

一、空间曲线的切线与法平面 过点 M 与切线垂直的平面称为曲线在该点的法 机动 目录 上页 下页 返回 结束 位置.  T M  空间光滑曲线在点 M 处的切线为此点处割线的极限 平面

1.曲线方程为参数方程的情况 T:x=p(),y=Ψ(t),2=0() 设t=t对应M(x0,y0,20) t=t0+△t对应M'(x,+△x,y0+Ay,0+△) 割线MM'的方程： x-0=y-y0=2-z0 △x △y △z 上述方程之分母同除以△1，令△t→0，得 切线方程 x-x0=y-0=2-0 o'(o)w'(o) o'(t） 下页返回结束

1. 曲线方程为参数方程的情况 切线方程 0 0 0 x x y y z − z = − = − ( , , ) 0 0 0 0 设 t = t 对应M x y z ( , , ) 0 0 0 0 t = t + t 对应 M  x + x y + y z + z ( ) 0  t ( ) 0  t ( ) 0  t 机动 目录 上页 下页 返回 结束T M  割线 MM 的方程 :

此处要求0'(to),w'(to),0'(to不全为0， 如个别为0，则理解为分子为0. 切线的方向向量： T=(o'(t),'(o),0'(o》 称为曲线的切向量 T也是法平面的法向量，因此得法平面方程 p(o)(x-x)+V'(0)(y-yot0'(0)(z-20)=0 说明：若引进向量函数r()=(o(),y(t),o(t),则T 为r(①的矢端曲线，而在t处的导向量 r(to)=(p'(to),w'(4o),0'(o)》 就是该点的切向量

( )( ) 0 0  t x − x 此处要求 ( ), ( ), ( ) 0 0 0  t  t  t 也是法平面的法向量, 切线的方向向量: 称为曲线的切向量 . ( )( ) 0 0 + t y − y ( )( ) 0 + t0 z − z0 = 如个别为0, 则理解为分子为 0 . 机动 目录 上页 下页 返回 结束  M  不全为0, ( ( ), ( ), ( )) 0 0 0 T =  t  t  t 因此得法平面方程 说明: 若引进向量函数 r(t) = ((t), (t), (t)) , 则  为 r (t) 的矢端曲线, 0 而在 t 处的导向量 ( ) ( ( ), ( ), ( )) 0 0 0 0 r  t =  t  t  t 就是该点的切向量. o r(t) T

*一元向量值函数及其导数 x=f(t) 空间曲线的参数方程： y=f0t∈[a] 之=f5() 记F=xi+yj+zk f(t)=f(t)i+f,(t)j+f(t)k 则空间曲线方程可写成向量形式： F=f)t∈[a,] 元向量值函数 定义了个映射了：[a,B]→R

*一元向量值函数及其导数 r f t = ( ) r x i y j zk = + +t   ，  空间曲线的参数方程： 1 2 3 ( ) ( ) ( ) x f t y f t z f t  =   =  =  t   ，  1 2 3 f t f t i f t j f t k ( ) ( ) ( ) ( ) = + + 记 则空间曲线方程可写成向量形式：   3 f R :   → 定义了 一个映射 ， → 一元向量值函数

定义 映射疗：DR”(DcR) 记作：产=f() 定义域D、自变量k、因变量r 向量值函数、数量值函数 在R3中：f(t)=f)i+f2(t)j+f5(t)k t∈D f(t)=((t),(t),f(t))teD

: n f D R → 定义 映射 → ( ) D R  记作： r f t = ( ) 定义域D、自变量t、因变量 r 向量值函数、数量值函数 在 R 3 中： 1 2 3 f t f t i f t j f t k ( ) ( ) ( ) ( ) = + + 1 2 3 或 f t f t f t f t ( ) ( ( ), ( ), ( )) = t D  t D 

向量值函数的终端曲线：向量r=f(t)终点M的轨迹 .曲线的向量方程f(t)=(f(t),f2(t),3(t)t∈D ·向量值函数的极限imf(t)=。 t→to f0=（m④，m0,w/,0》 x→to x→to x→t ·向量值函数的连续mf(t)=f(,) t→to 向量值函数的导数 lim f(+△)-f() dt -→0△t △t→0 △t

•向量值函数的终端曲线: •向量值函数的极限 •向量值函数的连续 •向量值函数的导数 0 0 lim ( ) t t f t r → = 0 0 0  →  → 0 0  +  −  = =   ( ) ( ) ( ) lim lim t t dr r f t t f t f t dt t t 或 0 0 lim ( ) ( ) t t f t f t → = 0 0 0 0 1 2 3 lim ( ) ( lim ( ), lim ( ), lim ( )) x t x t x t x t f t f t f t f t → → → → = 向量 •曲线的向量方程 1 2 3 f t f t f t f t ( ) ( ( ), ( ), ( )) = t D  r f t = ( ) 终点M的轨迹.  o f t( ) M

f'(t)=((),分'(t),f'()导向量 向量值函数的求导法则： (Cy'=0(C为常向量) (c0'=c(c为常数) (u士)'=± =+aw香r=以p+了 dt 话x可=ixr+ix了 a4pe1=ptuaota)

•向量值函数的求导法则： ( ) cu cu   = ( ) u v u v  =     [ ] d uv u v uv dt = +   ( ) C  = 0 [ ] d u v u v u v dt  =  +    [ ] d u v u v u v dt  =  +    [ ( )] ( ) ( ( )) d u t t u t dt    =  ( c为常数 ) ( C 为常向量 ) 1 2 3 f t f t f t f t ( ) ( ( ), ( ), ( ))     = 导向量

向量值函数下=f(t)导向量的几何意义： (t)=lim=lim(t+)4 △i-0△t△-→0 △t '() 向量值函数7=f()=0M的终端 △t 曲线在点处的一个切向量， △ f(t+△t) f(to) ·向量值函数下=f(t)导向量的物理意义： d (t)= 是质点M的速度向量，其方向 与曲线相切. d而d27 (t)= 是质点M的加速度向量， dt

•向量值函数 r f t = ( ) 导向量的几何意义： 向量值函数 r f t OM = = ( ) 的终端 曲线在点M处的一个切向量. •向量值函数 r f t = ( ) 导向量的物理意义： ( ) dr v t dt = 是质点M的速度向量，其方向 与曲线相切. 2 2 ( ) dv d r a t dt dt = = 是质点M的加速度向量. 0 f t ( )o 0 f t( )  M 0 0 0  →  → 0 0  +  −  = =   ( ) ( ) ( ) lim lim t t r f t t f t f t t t r f t t ( ) 0 +    r t