《离散数学》课程教学资源（教案讲义）第一章 命题逻辑

离散数学教案 《离散数学》课程教学教案 内蒙古农业大学计算机与信息工程学院 《离散数学》课程建设组

离散数学教案 1 《离散数学》课程教学教案 内蒙古农业大学计算机与信息工程学院 《离散数学》课程建设组

离散数学教案 《离散数学（一）》教学教案 第一部分课程总论 一、课程简介 课程名称：离散数学 英文名称：Discrete Mathematics 离散数学：离散数学是现代数学的一个重要分支，是计算机科学的核心课程。以 研究离散量的结构和相互间的关系为主要目标，其研究对象是有限个或无限个元素。 离散数学与计算机科学中的数据结构、操作系统、编译理论、算法分析、逻辑设计、 系统结构、容错诊断、机器定理证明等课程紧密相关。是一门重要的基础课程。 数学内容：数理逻辑、集合论、代数系统和图论和共四部分。 数学要求：通过该课程的学习，培养和锻炼抽象思维和缜密概括的能力，为专业 基础课和专业课的学习打下坚实的理论基础。 授课总学时：4学时/周×16周=64学时 二、适用对象 本课程教学教案主要针对计算机科学与技术和网络工程本科专业 三、学习要领 概念（正确）：必须掌握好离散数学中大量的概念 判断（准确）：根据概念对事物的属性进行判断 推理（可靠）：根据多个判断推出一个新的判断 四、离散数学与计算机的关系 第一部分数理逻辑 计算机是数理逻辑和电子学相结合的产物 第二部分集合论 集合：一种重要的数据结构 关系：关系数据库的理论基础 函数：所有计算机语言中不可缺少的一部分 第三部分代数系统 计算机编码和纠错码理论 数字逻辑设计基础 计算机使用的各种运算 第四部分图论 2

离散数学教案 2 《离散数学（一）》教学教案 第一部分 课程总论 一、课程简介 课程名称：离散数学 英文名称：Discrete Mathematics 离散数学：离散数学是现代数学的一个重要分支，是计算机科学的核心课程。以 研究离散量的结构和相互间的关系为主要目标，其研究对象是有限个或无限个元素。 离散数学与计算机科学中的数据结构、操作系统、编译理论、算法分析、逻辑设计、 系统结构、容错诊断、机器定理证明等课程紧密相关。是一门重要的基础课程。 教学内容：数理逻辑、集合论、代数系统和图论和共四部分。 教学要求：通过该课程的学习，培养和锻炼抽象思维和缜密概括的能力，为专业 基础课和专业课的学习打下坚实的理论基础。 授课总学时： 4 学时/周  16 周 = 64 学时 二、适用对象 本课程教学教案主要针对计算机科学与技术和网络工程本科专业 三、学习要领 概念（正确）：必须掌握好离散数学中大量的概念 判断（准确）：根据概念对事物的属性进行判断 推理（可靠）：根据多个判断推出一个新的判断 四、离散数学与计算机的关系 第一部分 数理逻辑 计算机是数理逻辑和电子学相结合的产物 第二部分 集合论 集合：一种重要的数据结构 关系：关系数据库的理论基础 函数：所有计算机语言中不可缺少的一部分 第三部分 代数系统 计算机编码和纠错码理论 数字逻辑设计基础 计算机使用的各种运算 第四部分 图论

离散数学教案 数据结构、操作系统、编译原理、计算机网络原理的基础 五、教材及主要参考书 教材： 左孝凌、李为鑑、刘永才，离散数学，上海科学技术出版社，1982年9月第1 版。 参考书： [1)王元元、张桂芸，离散数学导论，科学出版社，2002 [2]Kenneth H.Rosen Discrete Mathematics and Its Applications Fourth Edition),机械工业出版社（华章），2001 [3)】王元元、张桂芸，计算机科学中的离散结构，机械工业出版社，2004 [4]Bernard Kolman,Robert C.Busby,Sharon Ross,Discrete Mathematical Structures(Fourth Edition),高等教育出版社，2O01 [⑤)孙吉贵杨凤杰欧阳丹彤李占山，离散数学，高等教育出版社，2002 [6马振华，离散数学导引，清华大学出版社，1993 [7)王树禾，离散数学引论，中国科技大学出版社，2001 [8]Andrew Simpon著冯速译离散数学导学机械工业出版社2005

离散数学教案 3 数据结构、操作系统、编译原理、计算机网络原理的基础 五、教材及主要参考书 教材： 左孝凌、李为鑑、刘永才，离散数学，上海科学技术出版社，1982 年 9 月第 1 版。 参考书： [1] 王元元、张桂芸，离散数学导论，科学出版社，2002 [2] Kenneth H.Rosen Discrete Mathematics and Its Applications ( Fourth Edition), 机械工业出版社(华章)，2001 [3] 王元元、张桂芸，计算机科学中的离散结构，机械工业出版社，2004 [4] Bernard Kolman , Robert C. Busby, Sharon Ross, Discrete Mathematical Structures (Fourth Edition), 高等教育出版社，2001 [5] 孙吉贵 杨凤杰 欧阳丹彤 李占山，离散数学， 高等教育出版社，2002 [6] 马振华，离散数学导引 ，清华大学出版社，1993 [7] 王树禾，离散数学引论，中国科技大学出版社，2001 [8] Andrew Simpon 著 冯速译 离散数学导学 机械工业出版社 2005

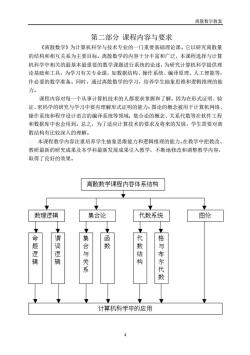
离散数学教案 第二部分课程内容与要求 《离散数学》为计算机科学与技术专业的一门重要基础理论课。它以研究离散量 的结构和相互关系为主要目标。离散数学的内容十分丰富和广泛，本课程选择与计算 机科学中相关的最基本最重要的数学课题进行系统的论述，为研究计算机科学提供理 论基础和工具，为学习有关专业课，如数据结构、操作系统、编译原理、人工智能等， 作必要的数学准备。同时，通过离散数学的学习，培养学生抽象思维和逻辑推理的能 力。 课程内容对每一个从事计算机技术的人都要求掌握和了解。因为在形式证明、验 证、密码学的研究与学习中要有理解形式证明的能力：图论的概念被用于计算机网络 操作系统和程序设计语言的编译系统等领域：集合论的概念、关系代数等在软件工程 和数据库中也会用到。总之，为了适应计算技术的要求及将来的发展，学生需要对离 散结构有比较深入的理解。 本课程教学内容注重培养学生抽象思维能力和逻辑推理的能力。在教学中把教改、 教研最新的研究成果及本学科最新发展成果引入教学，不断地修改和调整教学内容， 取得了良好的效果。 离散数学课程内容体系结构 数理逻辑 集合论 代数系统 图伦 命 谓 名 数 逻 逻 辑 辑 关 数结构 布尔 计算机科学中的应用

离散数学教案 4 第二部分 课程内容与要求 《离散数学》为计算机科学与技术专业的一门重要基础理论课。它以研究离散量 的结构和相互关系为主要目标。离散数学的内容十分丰富和广泛，本课程选择与计算 机科学中相关的最基本最重要的数学课题进行系统的论述，为研究计算机科学提供理 论基础和工具，为学习有关专业课，如数据结构、操作系统、编译原理、人工智能等， 作必要的数学准备。同时，通过离散数学的学习，培养学生抽象思维和逻辑推理的能 力。 课程内容对每一个从事计算机技术的人都要求掌握和了解。因为在形式证明、验 证、密码学的研究与学习中要有理解形式证明的能力；图论的概念被用于计算机网络、 操作系统和程序设计语言的编译系统等领域；集合论的概念、关系代数等在软件工程 和数据库中也会用到。总之，为了适应计算技术的要求及将来的发展，学生需要对离 散结构有比较深入的理解。 000 本课程教学内容注重培养学生抽象思维能力和逻辑推理的能力。在教学中把教改、 教研最新的研究成果及本学科最新发展成果引入教学，不断地修改和调整教学内容， 取得了良好的效果

离散数学教案 第一篇数理逻辑 逻辑学(1ogic) 是一门研究思维形式及思维规律的科学 数理逻辑(thematical logic) 是用数学的方法来研究人类推理过程的一门数学学科。 其显著特征是符号化和形式化，即把逻辑所涉及的“概念、判断、推理”用符号 来表示，用公理体系来刻划，并基于符号串形式的演算来描述推理过程的一般规律。 数理逻辑又称符号逻辑、现代逻辑。 命题逻辑 一、学习目的与要求 本章目的是介绍命题逻辑的基本概念。掌握利用命题逻辑表示自然语言，描述概 念、判断和推理。建立初步的语言形式化方法。 二、知识点 1.命题的概念、表示方法：联结词的逻辑意义。 2.命题公式的递归定义，自然语言翻译成命题公式 3.真值表的构造、命题公式等价的概念。 4.重言式与蕴涵式的定义、逻辑意义，逻辑等价与逻辑蕴涵的意义和证明方法。 常用的逻辑等价公式和逻辑蕴涵公式。 5.命题公式的对偶式、合取范式、析取范式、主合取范式、主析取范式。逻辑 小项、逻辑大项。任给公式化为析取范式、任给公式化为主析取范式、任给公式化为 合取范式、任给公式化为主合取范式。 6.命题逻辑的推理理论，主要的推理方法：真值表法、直接证明法、间接证明 法。常用推理规则：P规则、T规则、CP规则。 7.命题逻辑的应用示例。 三、要求 1.识记 命题表示方法、真值判断、命题公式的递归定义。 2.领会 联结词真值确定、翻译、命题公式的等价性和蕴涵性证明、任给公式化为析取范 式、任给公式化为主析取范式、任给公式化为合取范式、任给公式化为主合取范式。 3.简单应用 命题逻辑推理规则，命题逻辑设计简单的开关电路。 四、主要内容

离散数学教案 5 第一篇 数理逻辑 逻辑学（ logic ） 是一门研究思维形式及思维规律的科学。 数理逻辑（mathematical logic) 是用数学的方法来研究人类推理过程的一门数学学科。 其显著特征是符号化和形式化，即把逻辑所涉及的“概念、判断、推理”用符号 来表示，用公理体系来刻划, 并基于符号串形式的演算来描述推理过程的一般规律。 数理逻辑又称符号逻辑、现代逻辑。 命题逻辑 一、学习目的与要求 本章目的是介绍命题逻辑的基本概念。掌握利用命题逻辑表示自然语言，描述概 念、判断和推理。建立初步的语言形式化方法。 二、知识点 1．命题的概念、表示方法；联结词的逻辑意义。 2．命题公式的递归定义，自然语言翻译成命题公式 3．真值表的构造、命题公式等价的概念。 4．重言式与蕴涵式的定义、逻辑意义，逻辑等价与逻辑蕴涵的意义和证明方法。 常用的逻辑等价公式和逻辑蕴涵公式。 5．命题公式的对偶式、合取范式、析取范式、主合取范式、主析取范式。逻辑 小项、逻辑大项。任给公式化为析取范式、任给公式化为主析取范式、任给公式化为 合取范式、任给公式化为主合取范式。 6．命题逻辑的推理理论，主要的推理方法：真值表法、直接证明法、间接证明 法。常用推理规则：P 规则、T 规则、CP 规则。 7．命题逻辑的应用示例。 三、要求 1．识记 命题表示方法、真值判断、命题公式的递归定义。 2．领会 联结词真值确定、翻译、命题公式的等价性和蕴涵性证明、任给公式化为析取范 式、任给公式化为主析取范式、任给公式化为合取范式、任给公式化为主合取范式。 3．简单应用 命题逻辑推理规则，命题逻辑设计简单的开关电路。 四、主要内容

离散数学教案 第1章命题逻辑 命题逻辑，也称命题演算，记为L5。它与谓词逻辑构成数理逻辑的基础，而命 题逻辑又是谓词逻辑的基础。数理逻辑是用数学方法即通过引入表意符号研究推理的 学问。因此，数理逻辑又名为符号逻辑。 命题逻辑是研究由命题为基本单位构成的前提和结论之间的可推导关系。 1.1命题与联结词 1,命题的概念 所谓命题，是指具有非真必假的陈述句。而疑问句、析使句和感叹句等因都不能 判断其真假，故都不是命题。命题仅有两种可能的真值一真和假，且二者只能居其一。 真用1或T表示，假用0或F表示。由于命题只有两种真值，所以称这种逻辑为二值 逻辑。命题的真值是具有客观性质的，而不是由人的主观决定的。 如果一陈述句再也不能分解成更为简单的语句，由它构成的命题称为原子命题。 原子命题是命题逻辑的基本单位。 命题分为两类： 第一类是原子命题，原子命题用大写英文字母P,Q,R.及其带下标的Pi,Qi, Ri,.表示。 第二类是复合命题，它由原子命题、命题联结词和圆括号组成。 2,命题联结词 定义1.1.1设P表示一个命题，由命题联结词和命题P连接成幻P,称P 为P的否定式复合命题，一P读“非P”。称幻为否定联结词。P是真，当且仅当 P为假：7P是假，当且仅当P为真。否定联结词“”的定义可由表1.1.1表示之。 由于否定”修改了命题，它是对单个命题进行操作，称它为一元联结词。 定义1.1.2设P和Q为两个命题，由命题联结词八将P和Q连接成P∧Q,称P 八Q为命题P和Q的合取式复合命题，P人Q读做“P与Q”,或“P且Q”。称∧为合 取联结词。 当且仅当P和Q的真值同为真，命题PAQ的真值才为真：否则，PAQ的真值为 假。合取联结词八的定义由表1.1.2表示之。 定义1.1.3设P和Q为两个命题，由命题联结词V把P和Q连接成PVQ,称P VQ为命题P和Q的析取式复合命题，PVQ读做“P或Q”。称V为析取联结词。 6

离散数学教案 6 第 1 章 命题逻辑 命题逻辑，也称命题演算，记为 Ls。它与谓词逻辑构成数理逻辑的基础，而命 题逻辑又是谓词逻辑的基础。数理逻辑是用数学方法即通过引入表意符号研究推理的 学问。因此，数理逻辑又名为符号逻辑。 命题逻辑是研究由命题为基本单位构成的前提和结论之间的可推导关系。 1.1 命题与联结词 １. 命题的概念 所谓命题，是指具有非真必假的陈述句。而疑问句、祈使句和感叹句等因都不能 判断其真假，故都不是命题。命题仅有两种可能的真值—真和假，且二者只能居其一。 真用 1 或 T 表示，假用 0 或 F 表示。由于命题只有两种真值，所以称这种逻辑为二值 逻辑。命题的真值是具有客观性质的，而不是由人的主观决定的。 如果一陈述句再也不能分解成更为简单的语句，由它构成的命题称为原子命题。 原子命题是命题逻辑的基本单位。 命题分为两类： 第一类是原子命题，原子命题用大写英文字母 P，Q，R.及其带下标的 Pi，Qi， Ri，.表示。 第二类是复合命题，它由原子命题、命题联结词和圆括号组成。 ２. 命题联结词 定义 1.1.1 设 P 表示一个命题，由命题联结词┐和命题 P 连接成┐P，称┐P 为 P 的否定式复合命题， ┐P 读“非 P”。称┐为否定联结词。┐P 是真，当且仅当 P 为假；┐P 是假，当且仅当 P 为真。否定联结词“┐”的定义可由表 1.1.1 表示之。 由于否定”修改了命题，它是对单个命题进行操作，称它为一元联结词。 定义 1.1.2 设 P 和 Q 为两个命题，由命题联结词∧将 P 和 Q 连接成 P∧Q，称 P ∧Q 为命题 P 和 Q 的合取式复合命题，P∧Q 读做“P 与 Q”，或“P 且 Q”。称∧为合 取联结词。 当且仅当 P 和 Q 的真值同为真，命题 P∧Q 的真值才为真；否则，P∧Q 的真值为 假。合取联结词∧的定义由表 1.1.2 表示之。 定义 1.1.3 设 P 和 Q 为两个命题，由命题联结词∨把 P 和 Q 连接成 P∨Q，称 P ∨Q 为命题 P 和 Q 的析取式复合命题，P∨Q 读做“P 或 Q”。称∨为析取联结词

离散数学教案 当且仅当P和Q的真值同为假，PVQ的真值为假：否则，PVQ的真值为真。析取联 结词V的定义由表1.1.3表示之。 由定义可知，析取联结词表示“可兼和”，“不可兼和”另有别的联结词定义之。 与合取联结词一样，使用析取联结词时，也不要求两命题间一定有任何关系，有 关例子就不再给出了。 定义1.1.4设P和Q为两个命题，由命题联结词→把P和Q连接成P→Q,称P →Q为命题P和Q的条件式复合命题，简称条件命题。P→Q读做“P条件Q”或者“若 P则Q”。称一为条件联结词。 当P的真值为真而Q的真值为假时，命题P→Q的真值为假：否则，P一Q的真值 为真。条件联结词一的定义由表1.1.4表示之。 在条件命题P→Q中，命题P称为P→Q的前件或前提，命题Q称为P→Q的后件 或结论。条件命题P一Q有多种方式陈述：“如果P,那么Q”:“P仅当Q”:“Q 每当P”:“P是Q的充分条件”：“Q是P的必要条件”等。 在日常生活中，用条件式表示前提和结论之间的因果或实质关系，如例1.1.4中 的①，这种条件式称为形式条件命题。然而在命题逻辑中，一个条件式的前提并不要 求与结论有任何关系，这种条件式称为实质条件命题。采用实质条件式作定义，不单 是出于“善意推断”，主要是因为前提与结论间有无因果和实质关系难以区分，而且 实质条件式己包含了形式条件式，更便于应用。 定义1.1.5令P、Q是两个命题，由命题联结词把P和Q连接成P)Q,称 P一Q为命题P和Q的双条件式复合命题，简称双条件命题，P行Q读做“P当且 仅当Q”,或“P等价Q”。称→为双条件联结词。 当P和Q的真值相同时，P:Q的真值为真：否则，PQ的真值为假。双条 件联结词的定义由表1.1.5表示之。 在本节结束时，应强调指出的是：复合命题的真值只取决于各原子命题的真值， 而与它们的内容、含义无关，与原子命题之间是否有关系无关。理解和掌握这一点是 至关重要的，请读者认真去领会。 1.2命题变元和合式公式 1.命题变元

离散数学教案 7 当且仅当 P 和 Q 的真值同为假，P∨Q 的真值为假；否则，P∨Q 的真值为真。析取联 结词∨的定义由表 1.1.3 表示之。 由定义可知，析取联结词表示“可兼和”，“不可兼和”另有别的联结词定义之。 与合取联结词一样，使用析取联结词时，也不要求两命题间一定有任何关系，有 关例子就不再给出了。 定义 1.1.4 设 P 和 Q 为两个命题，由命题联结词→把 P 和 Q 连接成 P→Q，称 P →Q 为命题 P 和 Q 的条件式复合命题，简称条件命题。P→Q 读做“P 条件 Q”或者“若 P 则 Q”。称→为条件联结词。 当 P 的真值为真而 Q 的真值为假时，命题 P→Q 的真值为假；否则，P→Q 的真值 为真。条件联结词→的定义由表 1.1.4 表示之。 在条件命题 P→Q 中，命题 P 称为 P→Q 的前件或前提，命题 Q 称为 P→Q 的后件 或结论。条件命题 P→Q 有多种方式陈述：“如果 P，那么 Q”；“P 仅当 Q”；“Q 每当 P”；“P 是 Q 的充分条件”；“Q 是 P 的必要条件”等。 在日常生活中，用条件式表示前提和结论之间的因果或实质关系，如例 1.1.4 中 的①，这种条件式称为形式条件命题。然而在命题逻辑中，一个条件式的前提并不要 求与结论有任何关系，这种条件式称为实质条件命题。采用实质条件式作定义，不单 是出于“善意推断”，主要是因为前提与结论间有无因果和实质关系难以区分，而且 实质条件式已包含了形式条件式，更便于应用。 定义 1.1.5 令 P、Q 是两个命题，由命题联结词把 P 和 Q 连接成 P  Q，称 P  Q 为命题 P 和 Q 的双条件式复合命题，简称双条件命题，P  Q 读做“P 当且 仅当 Q”，或“P 等价 Q”。称为双条件联结词。 当 P 和 Q 的真值相同时，P  Q 的真值为真；否则，P  Q 的真值为假。双条 件联结词的定义由表 1.1.5 表示之。 在本节结束时，应强调指出的是：复合命题的真值只取决于各原子命题的真值， 而与它们的内容、含义无关，与原子命题之间是否有关系无关。理解和掌握这一点是 至关重要的，请读者认真去领会。 1.2 命题变元和合式公式 １. 命题变元

离散数学教案 在命题逻辑中，命题又有命题常元和命题变元之分。一个确定的具体的命题，称 为命题常元：一个不确定的泛指的任意命题，称为命题变元。显然，命题变元不是命 题，只有用一个特定的命题取代才能确定它的真值：真或假。这时也说对该命题变元 指派真值。 命题常元和命题变元均可用字母P等表示。由于在命题逻辑中并不关心具体命题 的涵义，只关心其真值，因此，可以形式地定义它们如下： 定义1.2.1以真或1、假或0为其变域的变元，称为命题变元：真或1、假或 0称为命题常元。 2.合式公式 通常把含有命题变元的断言称为命题公式。但这没能指出命题公式的结构，因为 不是所有由命题变元、联结词和括号所组成的字符串都能成为命题公式。为此常使用 归纳定义命题公式，以便构成的公式有规则可循。由这种定义产生的公式称为合式公 式。 定义1.2.2单个命题变元和命题常元称为原子命题公式，简称原子公式。 定义1.2.3合式公式是由下列规则生成的公式： ①单个原子公式是合式公式。 ②若A是一个合式公式，则(IA)也是一个合式公式。 ③若A、B是合式公式，则(AAB)、(AVB)、(A→B)和(AB)都是合式公式 ④只有有限次使用①、②和③生成的公式才是合式公式。 当合式公式比较复杂时，常常使用很多圆括号，为了减少圆括号的使用量，可作 以下约定： ①规定联结词的优先级由高到低的次序为：一、八、V、→、→ ②相同的联结词按从左至右次序计算时，圆括号可省略。 ③最外层的圆括号可以省略。 为了方便计，合式公式也简称公式。 3.公式真值表 定义1.2.4对于公式中命题变元的每一种可能的真值指派，以及由它们确定出 的公式真值所列成的表，称为该公式的真值表。 定义1.2.5如果B是公式A中的一部分，且B为公式，则称B是公式A的子公

离散数学教案 8 在命题逻辑中，命题又有命题常元和命题变元之分。一个确定的具体的命题，称 为命题常元；一个不确定的泛指的任意命题，称为命题变元。显然，命题变元不是命 题，只有用一个特定的命题取代才能确定它的真值：真或假。这时也说对该命题变元 指派真值。 命题常元和命题变元均可用字母 P 等表示。由于在命题逻辑中并不关心具体命题 的涵义，只关心其真值，因此，可以形式地定义它们如下： 定义 1.2.1 以真或 1、假或 0 为其变域的变元，称为命题变元；真或 1、假或 0 称为命题常元。 2. 合式公式 通常把含有命题变元的断言称为命题公式。但这没能指出命题公式的结构，因为 不是所有由命题变元、联结词和括号所组成的字符串都能成为命题公式。为此常使用 归纳定义命题公式，以便构成的公式有规则可循。由这种定义产生的公式称为合式公 式。 定义 1.2.2 单个命题变元和命题常元称为原子命题公式，简称原子公式。 定义 1.2.3 合式公式是由下列规则生成的公式： ①单个原子公式是合式公式。 ②若 A 是一个合式公式，则(lA)也是一个合式公式。 ③若 A、B 是合式公式，则(A∧B)、(A∨B)、(A→B)和(A  B)都是合式公式。 ④只有有限次使用①、②和③生成的公式才是合式公式。 当合式公式比较复杂时，常常使用很多圆括号，为了减少圆括号的使用量，可作 以下约定： ①规定联结词的优先级由高到低的次序为：┐、∧、∨、→、  ②相同的联结词按从左至右次序计算时，圆括号可省略。 ③最外层的圆括号可以省略。 为了方便计，合式公式也简称公式。 ３. 公式真值表 定义 1.2.4 对于公式中命题变元的每一种可能的真值指派，以及由它们确定出 的公式真值所列成的表，称为该公式的真值表。 定义 1.2.5 如果 B 是公式 A 中的一部分，且 B 为公式，则称 B 是公式 A 的子公

离散数学教案 式。 用归纳法不难证明，对于含有个命题变元的公式，有2个真值指派，即在该公 式的真值表中有2n行。 为方便构造真值表，特约定如下： ①命题变元按字典序排列。 ②对每个指派，以二进制数从小到大或从大到小顺序列出。 ③若公式较复杂，可先列出各子公式的真值（若有括号，则应从里层向外层展 开)，最后列出所求公式的真值。 4.命题的符号化 把一个用文字叙述的命题相应地写成由命题标识符、联结词和圆括号表示的合式 公式，称为命题的符号化。符号化应该注意下列事项： ①确定给定句子是否为命题。 ②句子中连词是否为命题联结词。 ③要正确地表示原子命题和适当选择命题联结词。 命题符号化是很重要的，一定要掌握好，在命题推理中常常最先遇到的就是符号 化一个问题，解决不好，等于说推理的首要前提没有了。 1.3公式分类与等价公式 1,公式分类 定义1.3.1设A为任意公式，则 ①对应每一个指派，公式A均相应确定真值为真，称A为重言式，或永真式。 ②对应每一个指派，公式A均相应确定真值为假，称A为矛盾式，或永假式。 ③至少存在一个指派，公式A相应确定真值为真，称A为可满足式。 由定义可知，重言式必是可满足式，反之一般不真。 重点将研究重言式，它最有用，因为它有以下特点： ①重言式的否定是矛盾式，矛盾式的否定是重言式，这样只研究其一就可以了。 ②两重言式的合取式、析取式、条件式和双条件式等都仍是重言式。于是，由简 单的重言式可构造出复杂的重言式。 ③由重言式使用公认的规则可以产生许多有用等价式和蕴涵式。 判定给定公式是否为永真式、永假式或可满足式的问题，称为给定公式的判定问

离散数学教案 9 式。 用归纳法不难证明，对于含有 n 个命题变元的公式，有 2 n 个真值指派，即在该公 式的真值表中有 2n 行。 为方便构造真值表，特约定如下： ① 命题变元按字典序排列。 ② 对每个指派，以二进制数从小到大或从大到小顺序列出。 ③ 若公式较复杂，可先列出各子公式的真值(若有括号，则应从里层向外层展 开)，最后列出所求公式的真值。 4. 命题的符号化 把一个用文字叙述的命题相应地写成由命题标识符、联结词和圆括号表示的合式 公式，称为命题的符号化。符号化应该注意下列事项: ① 确定给定句子是否为命题。 ② 句子中连词是否为命题联结词。 ③ 要正确地表示原子命题和适当选择命题联结词。 命题符号化是很重要的，一定要掌握好，在命题推理中常常最先遇到的就是符号 化一个问题，解决不好，等于说推理的首要前提没有了。 1.3 公式分类与等价公式 １. 公式分类 定义 1.3.1 设 A 为任意公式，则 ① 对应每一个指派，公式 A 均相应确定真值为真，称 A 为重言式，或永真式。 ② 对应每一个指派，公式 A 均相应确定真值为假，称 A 为矛盾式，或永假式。 ③ 至少存在一个指派，公式 A 相应确定真值为真，称 A 为可满足式。 由定义可知，重言式必是可满足式，反之一般不真。 重点将研究重言式，它最有用，因为它有以下特点： ①重言式的否定是矛盾式，矛盾式的否定是重言式，这样只研究其一就可以了。 ②两重言式的合取式、析取式、条件式和双条件式等都仍是重言式。于是，由简 单的重言式可构造出复杂的重言式。 ③由重言式使用公认的规则可以产生许多有用等价式和蕴涵式。 判定给定公式是否为永真式、永假式或可满足式的问题，称为给定公式的判定问

离散数学教案 免 在Ls中，由于任何一个命题公式的指派数目总是有限的，所以Ls的判定问题是 可解的。其判定方法有真值表法和公式推演法。 2,等价公式 定义1.3.2设A和B是两个命题公式，如果A、B在其任意指派下，其真值都 是相同的，则称A和B是等价的，或逻辑相等，记作A一B,读作A等价B,称A一B 为等价式。 显然，若公式A和B的真值表是相同的，则A和B等价。因此，验证两公式是否 等价，只需做出它们的真值表即可。 在这里，请读者注意和一的区别与联系。 区别：是逻辑联结词，属于目标语言中的符号，它出现在命题公式中：一不是 逻辑联结词，属于元语言中的符号，表示两个命题公式的一种关系，不属于这两个公 式的任何一个公式中的符号。 联系：可用下面定理表明之。 定理1.3.1A一B当且仅当AB是永真式。 有时也称A一B是永真双条件式。 等价式有下列性质： ①自反性，即对任意公式A,有A一A。 ②对称性，即对任意公式A和B,若A一B,则B一A。 ③传递性，即对任意公式A、B和C,若A一B、B一C,则A一C。 3.基本等价式—一命题定律 在判定公式间是否等价，有一些简单而又经常使用的等价式，称为基本等价式或 称命题定律。牢固地记住它并能熟练运用，是学好数理逻辑的关键之一，读者应该注 意到这一点。现将这些命题定律列出如下： (I)双否定：TA台A。 (2)交换律：AAB=BAA,AVBOBVA,AB=B)A。 (3)结合律：(AAB)AC≌A∧(B∧C), (AVB)VC≌AV(BVC), (A→B)C台A→(BC)。 10

离散数学教案 10 题。 在 Ls 中，由于任何一个命题公式的指派数目总是有限的，所以 Ls 的判定问题是 可解的。其判定方法有真值表法和公式推演法。 ２. 等价公式 定义 1.3.2 设 A 和 B 是两个命题公式，如果 A、B 在其任意指派下，其真值都 是相同的，则称 A 和 B 是等价的，或逻辑相等，记作 AB，读作 A 等价 B，称 AB 为等价式。 显然，若公式 A 和 B 的真值表是相同的，则 A 和 B 等价。因此，验证两公式是否 等价，只需做出它们的真值表即可。 在这里，请读者注意和的区别与联系。 区别：是逻辑联结词，属于目标语言中的符号，它出现在命题公式中；不是 逻辑联结词，属于元语言中的符号，表示两个命题公式的一种关系，不属于这两个公 式的任何一个公式中的符号。 联系：可用下面定理表明之。 定理 1.3.1 A  B 当且仅当 AB 是永真式。 有时也称 A  B 是永真双条件式。 等价式有下列性质： ① 自反性，即对任意公式 A，有 A  A。 ② 对称性，即对任意公式 A 和 B，若 A  B，则 B  A。 ③ 传递性，即对任意公式 A、B 和 C，若 A  B、B  C，则 A  C。 ３.基本等价式——命题定律 在判定公式间是否等价，有一些简单而又经常使用的等价式，称为基本等价式或 称命题定律。牢固地记住它并能熟练运用，是学好数理逻辑的关键之一，读者应该注 意到这一点。现将这些命题定律列出如下： (1)双否定：AA。 (2)交换律：A∧BB∧A，A∨BB∨A，ABBA。 (3)结合律：(A∧B)∧CA∧(B∧C)， (A∨B)∨CA∨(B∨C)， (AB)CA(BC)