《离散数学》课程教学资源（教案讲义）第六章 图论

《离散数学》课程教学教案 内蒙古农业大学计算机与信息工程学院 《离散数学》课程建设组

1 《离散数学》课程教学教案 内蒙古农业大学计算机与信息工程学院 《离散数学》课程建设组

图论 一、学习目的与要求 图论是近年来发展迅速而又应用广泛的一门学科。本章主要讲授 图论的基本概念和定理，重点是欧拉图与汉密尔顿图、平面图、树。 要求熟练掌握图的基本概念和定理并能够进行简单应用。 二、知识点 1图的基本概念： 2链（或路）与圈（或回路）： 3图的矩阵表示： 4欧拉图与汉密尔顿图 5平面图： 6对偶图与着色 7树与生成树： 8根树及其应用。 三、要求 1.识记 图和树相关的数据结构、算法和计数 2.领会 图的有关概念和表示以及计算中使用图和树构建的模型。 四、主要内容 图论 7-1图的基本概念 什么是图？可用一句话概括，即：图是用点和线来刻划离散事物集 合中的每对事物间以某种方式相联系的数学模型。因为它显得太抽象， 不便于理解，所以有必要给出另外的回答。下面便是把图作为代数结 构的一个定义。 一、图的定义 1、图的定义 定义7-1.1：一个图是一个三元组,其中V(G)={v1 v2.,vn为有限非空结点集合，V1称为结点，E(G)={e1,.,e 为有限的边集合，©：称为边，pc是从边集合E到结点对集合上的函数。 图可简记为：G=。 例1：G=<W(G),E(G),9c 2

2 图论 一、学习目的与要求 图论是近年来发展迅速而又应用广泛的一门学科。本章主要讲授 图论的基本概念和定理，重点是欧拉图与汉密尔顿图、平面图、树。 要求熟练掌握图的基本概念和定理并能够进行简单应用。 二、知识点 1 图的基本概念； 2 链(或路)与圈(或回路)； 3 图的矩阵表示； 4 欧拉图与汉密尔顿图 5 平面图； 6 对偶图与着色； 7 树与生成树； 8 根树及其应用。 三、要求 1．识记 图和树相关的数据结构、算法和计数 2．领会 图的有关概念和表示以及计算中使用图和树构建的模型。 四、主要内容 图论 7-1 图的基本概念 什么是图?可用一句话概括，即：图是用点和线来刻划离散事物集 合中的每对事物间以某种方式相联系的数学模型。因为它显得太抽象， 不便于理解，所以有必要给出另外的回答。下面便是把图作为代数结 构的一个定义。 一、图的定义 1、图的定义 定义 7-1.1：一个图是一个三元组，其中 V(G)={v1， v 2，.，v n }为有限非空结点集合，v i 称为结点，E(G)={e1，.，e m } 为有限的边集合，e i 称为边， G 是从边集合 E 到结点对集合上的函数。 图可简记为：G=。 例 1：G=

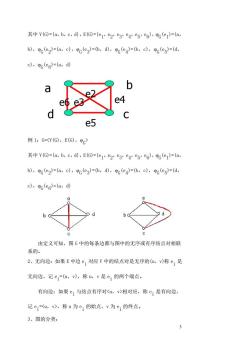
V(G)=(a,b,c,d),E(G)=(e,e2.eg,e es,es),G(e)=(a, b),PG(e2)=(a,c),G(e3)=(b,d),(e)=(b,c),(es)=(d, c),G(es)=(a,d) a b e5 例1：G=相对应，称e:是有向边， 记e:=u,v>,称u为e;的始点，v为e:的终点。 3、图的分类：

3 其中 V(G)={a，b，c，d}，E(G)={e1 ，e 2 ，e 3 ，e 4 ，e 5 ，e 6 }， G (e1 )=(a， b)， G (e2 )=(a，c)， G (e3 )=(b，d)， G (e4 )=(b，c)， G (e5 )=(d， c)， G (e6 )=(a，d) 例 1：G= 其中 V(G)={a，b，c，d}，E(G)={e1 ，e 2 ，e 3 ，e 4 ，e 5 ，e 6 }， G (e1 )=(a， b)， G (e2 )=(a，c)， G (e3 )=(b，d)， G (e4 )=(b，c)， G (e5 )=(d， c)， G (e6 )=(a，d) 由定义可知，图 G 中的每条边都与图中的无序或有序结点对相联 系的。 2、无向边：如果 E 中边 e i 对应 V 中的结点对是无序的(u，v)称 e i 是 无向边，记 e i =(u，v)，称 u，v 是 e i 的两个端点。 有向边：如果 e i 与结点有序对相对应，称 e i 是有向边， 记 e i =，称 u 为 e i 的始点，v 为 e i 的终点。 3、图的分类： a b d c e2 e3 e4 e5 e6

①无向图：每条边均为无向边的图称为无向图。 ②有向图：每条边均为有向边的图称为有向图。 ③混合图：有些边是无向边，有些边是有向边的图称为混合图。 见273页图7-1.2 (a)是无向图 (6)是有向图 (c)是混合图 练习：画出下面的图 (1)G1=是无向图，其中V1=W1,V2,V3,V4,V5,V6, E1={el,e2,e3,e4,e5,e6, e1=(W1,V3),e2=(W1,V4),e2=(W2,V4),e3=(W3,V4),e4=(W3, V6),e5=(W4,V5),e6=(W5,V6) (2)G2=是有向图，其中V2=(V1,V2,V3,V4},E={,,, ,,} (3)G3=是混合图，V3=W1,V2,V3,V4, E3={,(W1,V3),,,(W4,V2)} 4、点和边的关联：如e:=(u,v)或e=称u,v与e1关联 5、点与点的相邻：关联于同一条边的结点称为邻接点。 6、边与边的邻接：关联于同一结点的边称为邻接边。 7、孤立结点：不与任何结点相邻接的结点称为孤立结点。 8、零图：仅有孤立结点的图。 9、平凡图：仅有一个孤立结点的图。 10、自回路（环）：关联于同一结点的边称为自回路，或称为环。见274 页图7-1.3(c,c)是环 11、平行边：在有向图中，始点和终点均相同的边称为平行边，无向 图中若两点间有多条边，称这些边为平行边，两点间平行边的条数称 为边的重数。 二、点的度数 1、点的度数的定义 定义7-1.2：在图G=,v∈V,与结点v关联的边数称为该点的度 数，记为deg(w)。孤立结点的度数为0。 2、出度与入度 定义T-1.3:在有向图中，veV,以v为始点的边数称为该结点的出度， 记作deg(v):以v为终点的边数称为该结点的入度，记作deg(w)。 显然有deg(w)=deg(v)+deg(w) 4

4 ①无向图：每条边均为无向边的图称为无向图。 ②有向图：每条边均为有向边的图称为有向图。 ③混合图：有些边是无向边，有些边是有向边的图称为混合图。 见 273 页图 7-1.2 (a)是无向图 (b)是有向图 (c)是混合图 练习：画出下面的图。 （1）G1=是无向图，其中 V1={V1，V2，V3，V4，V5，V6}， E1={e1，e2，e3，e4，e5，e6}， e1=(V1，V3)，e2=(V1，V4)，e2=(V2，V4)，e3=(V3，V4)，e4=(V3， V6)，e5=(V4，V5)，e6=(V5，V6) （2）G2=是有向图，其中 V2={V1，V2，V3，V4}，E={，，，， ，，} （3）G3=是混合图，V3={V1，V2，V3，V4}， E3={，(V1，V3)，，，(V4，V2)} 4、点和边的关联：如 e i =(u，v)或 e i =称 u，v 与 e i 关联。 5、点与点的相邻：关联于同一条边的结点称为邻接点。 6、边与边的邻接：关联于同一结点的边称为邻接边。 7、孤立结点：不与任何结点相邻接的结点称为孤立结点。 8、零图：仅有孤立结点的图。 9、平凡图：仅有一个孤立结点的图。 10、自回路(环)：关联于同一结点的边称为自回路，或称为环。见 274 页图 7-1.3 (c,c)是环 11、平行边：在有向图中，始点和终点均相同的边称为平行边，无向 图中若两点间有多条边，称这些边为平行边，两点间平行边的条数称 为边的重数。 二、点的度数 1、点的度数的定义 定义 7-1.2：在图 G=，vV，与结点 v 关联的边数称为该点的度 数，记为 deg(v)。孤立结点的度数为 0。 2、出度与入度 定义 7-1.3：在有向图中，vV，以 v 为始点的边数称为该结点的出度， 记作 deg+ (v);以 v 为终点的边数称为该结点的入度，记作 deg- (v)。 显然有 deg(v)=deg+ (v)+deg- (v)

如：G1是无向图，deg(v1)=3,deg(v2)=1 G2是有向图，deg(w1)=3,deg(w1)=2,deg(v1)=5 v1 O -0v2 G1 v3 v4 G2 3、最大度和最小度： 图G最大度记为△(G)=max{deg(w)lveV(G)}, 最小度数记为8(G)=min{deg(w)lveV(G)}。 4、定理7-1.1：每个图中，结点度数总和等于边数的两倍。即 ∑deg(v)=2lEl 该定理又称握手定理 证明因为每条边必关联两个结点，而一条边给予关联的每个结点的 度数为1。因此在每个图中，结点度数总和等于边数的两倍。 5、定理7-1.2：在任何图中，度数为奇数的结点的个数必为偶数。 6、定理7-1.3：在任何有向图中，所有结点的入度之和等于所有结点 的出度之和。 证明因为每一条有向边必对应一个入度和一个出度，若一个结点具有 一个入度或出度，则必关联一条有向边，所以有向图中，各结点入度 之和等于边数，各结点出度之和也等于边数。因此，在任何有向图中， 所有结点的入度之和等于所有结点的出度之和。 三、特殊的图 1、多重图 定义7-1.4：含有平行边的图称为多重图。 2、简单图：不含平行边和环的图称为简单图。 3、完全图 定义7-1.5：简单图G=中，若每一对结点间均有边相连，则称 该图为完全图。 5

5 如：G1 是无向图，deg(v1)=3，deg(v2)=1 G2 是有向图，deg+ (v1)=3，deg- (v1)=2，deg(v1)=5， 3、最大度和最小度： 图 G 最大度记为 (G)=max{deg(v)|vV(G)}， 最小度数记为 (G)=min{deg(v)|vV(G)}。 4、定理 7-1.1：每个图中，结点度数总和等于边数的两倍。即 deg(v)=2|E| 该定理又称握手定理 证明 因为每条边必关联两个结点，而一条边给予关联的每个结点的 度数为 1。因此在每个图中，结点度数总和等于边数的两倍。 5、定理 7-1.2：在任何图中，度数为奇数的结点的个数必为偶数。 6、定理 7-1.3：在任何有向图中，所有结点的入度之和等于所有结点 的出度之和。 证明 因为每一条有向边必对应一个入度和一个出度，若一个结点具有 一个入度或出度，则必关联一条有向边，所以有向图中，各结点入度 之和等于边数，各结点出度之和也等于边数 。因此，在任何有向图中， 所有结点的入度之和等于所有结点的出度之和。 三、特殊的图 1、多重图 定义 7-1.4：含有平行边的图称为多重图。 2、简单图：不含平行边和环的图称为简单图。 3、完全图 定义 7-1.5：简单图 G=中，若每一对结点间均有边相连，则称 该图为完全图。 v1 v2 v1 v3 v4 v2 G1 G2

有n个结点的无向完全图记为K。 无向完全图：每一条边都是无向边，不含有平行边和环，每一对结点 间都有边相连 4、定理7-1.4：n个结点的无向完全图Kn的边数为n(n-1)/2。 如果在K中，对每一条边任意确定一个方向，则称该图为n个结点的 有向完全图。显然它的边数为n(-1)/2。 练习：279页(1) 证明在任何有向完全图中，所有结点入度的平方之和等于所有结点的 出度平方之和。 证明设有向完全图有n个结点。对于任意结点V;均有 deg"(vi)+deg(vi)=n-1 (1) 而有向完全图的边数为n(血-1)/2， 由定理7-1.1有∑deg(v;)+Σdeg(v;）=n(n-1) 由定理7-1.3有∑deg(w)=∑deg(v) 所以∑deg(v;)=∑deg(v)=n(n-1)/2(2) 由(1)有(deg(v)2-(m-1-deg(w)2 因此Σ(degw)2=∑(-l-degw))2 =[-1)2-2a-1)degw)+(degw:)3 Σ(degv)2=Σ(m-1-deg(v:)2 =x[m-)2-2(a-)degv)+(deg(w）)2] =n(n-1)2 -2n(n-1)Edeg (vi)+E deg (vi))2 =n(m-1)2-2(a-1)Σdeg(w)+Σ(deg(w))2 由(2)有∑deg(v)=n(-1)/2 代入上式即得 6

6 有 n 个结点的无向完全图记为 K n 。 无向完全图：每一条边都是无向边，不含有平行边和环，每一对结点 间都有边相连 4、定理 7-1.4：n 个结点的无向完全图 Kn 的边数为 n(n-1)/2。 如果在 Kn 中，对每一条边任意确定一个方向，则称该图为 n 个结点的 有向完全图。显然它的边数为 n(n-1)/2。 练习：279 页(1) 证明在任何有向完全图中，所有结点入度的平方之和等于所有结点的 出度平方之和。 证明 设有向完全图有 n 个结点。对于任意结点 vi 均有 deg+ (vi ) + deg- (vi ) = n-1 （1） 而有向完全图的边数为 n(n-1)/2， 由定理 7-1.1 有∑deg+ (vi ) + ∑ deg- (vi ) = n(n-1) 由定理 7-1.3 有∑deg+ (vi ) = ∑ deg- (vi ) 所以∑deg+ (vi ) = ∑ deg- (vi ) = n(n-1)/2 （2） 由（1）有(deg+ (vi ))2 = (n-1 - deg- (vi ) )2 因此∑(deg+ (vi ))2 = ∑ (n-1 - deg- (vi ) )2 = ∑[(n-1) 2 -2(n-1) deg- (vi ) +( deg- (vi ) )2 ] ∑(deg+ (vi ))2 = ∑ (n-1 - deg- (vi ) )2 = ∑[(n-1) 2 -2(n-1) deg- (vi ) + ( deg- (vi ) )2 ] = n(n-1) 2 –2n(n-1) ∑deg- (vi ) + ∑( deg- (vi ) )2 =n(n-1) 2 –2(n-1) ∑deg- (vi ) + ∑( deg- (vi ) )2 由（2）有 ∑ deg- (vi ) = n(n-1)/2 代入上式即得

Σ(degw)2=Σ（degw))2 6、子图 定义7-1.7：设图G=,如果有图G=,且E'cE,V' V,则称G'为G的子图。当V'=V时，则称G'为G的生成子图。 7、相对于图G的补图 定义7-1.8：设G'=是G=的子图，若给定另一个图G” =使得E”=E-E',且V”中仅包含E”的边所关联的结点， 则称G”是子图G'相对于图G的补图。 见图7-1.7图(c)是图b)相对于图(a)的补图。 8、同构 在图的定义中，强调的是结点集、边集以及边与结点的关联关系， 既没有涉及到联结两个结点的边的长度、形状和位置，也没有给出结 点的位置或者规定任何次序。因此，对于给定的两个图，在它们的图 形表示中，即在用小圆圈表示结点和用直线或曲线表示联结两个结点 的边的图解中，看起来很不一样，但实际上却是表示同一个图。因而， 引入两图的同构概念便是十分必要的了。 定义7-1.9：设图G=及图G'=,如果存在一一对应 的映射g:V1→v'且e=(w1,v)(或)是G'的一条边，则称 G与G'同构，记作G2G'。 由同构的定义可知，不仅结点之间要具有一一对应关系，而且要 求这种对应关系保持结点间的邻接关系。对于有向图的同构还要求保 持边的方向。 显然，两图的同构是相互的，即G1同构于G2,G2同构于G1 两图同构的一些必要条件： 1.结点数目相同： 2.边数相等： 3.度数相同的结点数目相等 以上几个条件不是两个图同构的充分条件。 同构必须是结点和边分别存在一一对应。 对应结点度数不同，所以两图不同构。 寻找一种简单有效的方法来判定图的同构，至今仍是图论中悬而 未决的重要课题。 7-2路与回路 在无向图（或有向图）的研究中，常常考虑从一个结点出发，沿者

7 ∑(deg+ (vi ))2 = ∑ ( deg- (vi ) )2 6、子图 定义 7-1.7：设图 G=，如果有图 G’=，且 E’E，V’ V，则称 G’为 G 的子图。当 V’=V 时，则称 G’为 G 的生成子图。 7、相对于图 G 的补图 定义 7-1.8：设 G’=是 G=的子图，若给定另一个图 G” =使得 E”=E-E’，且 V”中仅包含 E”的边所关联的结点， 则称 G”是子图 G’相对于图 G 的补图。 见图 7-1.7 图(c)是图(b)相对于图(a)的补图。 8、同构 在图的定义中，强调的是结点集、边集以及边与结点的关联关系， 既没有涉及到联结两个结点的边的长度、形状和位置，也没有给出结 点的位置或者规定任何次序。因此，对于给定的两个图，在它们的图 形表示中，即在用小圆圈表示结点和用直线或曲线表示联结两个结点 的边的图解中，看起来很不一样，但实际上却是表示同一个图。因而， 引入两图的同构概念便是十分必要的了。 定义 7-1.9：设图 G=及图 G’=，如果存在一一对应 的映射 g：vi→vi’且 e=(vi，vj )(或)是 G 的一条边，当且 仅当 e’=(g(vi )，g(vj ))(或)是 G’的一条边，则称 G 与 G’同构，记作 G ≌ G’。 由同构的定义可知，不仅结点之间要具有一一对应关系，而且要 求这种对应关系保持结点间的邻接关系。对于有向图的同构还要求保 持边的方向。 显然，两图的同构是相互的，即 G 1 同构于 G 2，G 2 同构于 G 1。 两图同构的一些必要条件： 1.结点数目相同； 2.边数相等； 3.度数相同的结点数目相等。 以上几个条件不是两个图同构的充分条件。 同构必须是结点和边分别存在一一对应。 对应结点度数不同，所以两图不同构。 寻找一种简单有效的方法来判定图的同构，至今仍是图论中悬而 未决的重要课题。 7-2 路与回路 在无向图(或有向图)的研究中，常常考虑从一个结点出发，沿着

一些边（或弧）连续移动而达到另一个指定结点，这种依次由结点和边 (或弧)组成的序列，便形成了链（或路）的概念。 学习本节要熟悉如下概念(23个)：路、路的长度、回路、迹、通路、 圈、连通、连通分支、点割集、割点、点连通度、边割集、割边、边 连通度、可达性、节点之间的距离、图的直径、单侧连通、强连通、 弱连通、强分图、单侧分图、弱分图。 掌握5个定理，一个推论。 一、路 1定义7-2.1：给定图G=W,BD,设vg.,vn∈Ve1e2., emE,其中e1是关联于结点1-1v1的边，交替序列v0e1Y12enn 称为联结vo到vn的路。 o和Vn分别称作路的起点和终点，边的数目n称作路的长度。当v0vn 时，这条路称作回路。 若一条路中所有的边©1©2，e均不相同，称作迹。 若一条路中所有的结点oV1,Vn均不相同，则称作通路。 闭的通路，即除VOV。外，其余的结点均不相同的路，就称作圈。 例如 el e2 e3 20 v3 e4 e5 e6 e7 40 0w5 e8 8

8 一些边(或弧)连续移动而达到另一个指定结点，这种依次由结点和边 (或弧)组成的序列，便形成了链(或路)的概念。 学习本节要熟悉如下概念(23个)：路、路的长度、回路、迹、通路、 圈、连通、连通分支、点割集、割点、点连通度、边割集、割边、边 连通度、可达性、节点之间的距离、图的直径、单侧连通、强连通、 弱连通、强分图、单侧分图、弱分图。 掌握5个定理，一个推论。 一、路 1、定义 7-2.1：给定图 G＝，设 v 0 ，v 1 ，.，v n V，e 1 ，e 2 ，.， e m E，其中 e i 是关联于结点 v i-1，v i 的边，交替序列 v 0 e 1 v 1 e 2.e n v n 称为联结 v 0 到 v n 的路。 v 0 和 v n 分别称作路的起点和终点，边的数目 n 称作路的长度。当 v 0 =v n 时，这条路称作回路。 若一条路中所有的边 e 1，e 2，.，e m 均不相同，称作迹。 若一条路中所有的结点 v 0 ，v 1 ，.，v n 均不相同，则称作通路。 闭的通路，即除 v 0 =v n 外，其余的结点均不相同的路，就称作圈。 例如

路：v1e2v3e3v2e3v3e4v2e6v5e7V3 迹：v5egv4e5v26v5e7V3e4v2 通路：v4egv56v2e1V1e2v3 圈：v2e1V1e23e7V5e6v2 在简单图中一条路v0112“enY由它的结点序列g1?,Vn 确定，所以简单图的路，可由其结点序列表示。在有向图中，结点数 大于一的一条路亦可由边序列e12en表示。 2、定理7-2.1：在一个具有n个结点的图中，如果从结点v:到v存 在一条路，则从结点v:到yk存在一条不多于1条边的路。 3、推论：在一个具有n个结点的图中，若从结点v;到vk存在一条路 则必存在一条从y;到"k而边数小于n的通路。 定理7-2.1的证明 如果从结点v:到y存在一条路，该路上的结点序列是vV k,如果在这条中有1条边，则序列中必有1+1个结点，若1>-1， 则必有结点Vs,它在序列中不止出现一次，即必有结点序列vVs. VsVk在路中去掉从Vs到vs的这些边，仍是v;到vk的一条路， 但此路比原来的路边数要少，如此重复进行下去，必可得到一条从] 到k的不多于1条边的路。 9

9 路：v1 e2 v3 e3 v2 e3 v3 e4 v2 e6 v5 e7 v3 迹：v5 e8 v4 e5 v2 e6 v5 e7 v3 e4 v2 通路：v4 e8 v5 e6 v2 e1 v1 e2 v3 圈：v2 e1 v1 e2 v3 e7 v5 e6 v2 在简单图中一条路 v 0 e 1 v 1 e 2 .e n v n ，由它的结点序列 v 0 ，v 1 ，.，v n 确定，所以简单图的路，可由其结点序列表示。在有向图中，结点数 大于一的—条路亦可由边序列 e 1 e 2.e n 表示。 2、定理 7-2.1：在一个具有 n 个结点的图中，如果从结点 v j 到 v k 存 在一条路，则从结点 v j 到 v k 存在一条不多于 n-1 条边的路。 3、推论：在一个具有 n 个结点的图中，若从结点 v j 到 v k 存在一条路， 则必存在一条从 v j 到 v k 而边数小于 n 的通路。 定理 7-2.1 的证明 如果从结点 v j 到 v k 存在一条路，该路上的结点序列是 vj.vi. vk，如果在这条中有 l 条边，则序列中必有 l+1 个结点，若 l>n-1， 则必有结点 vs，它在序列中不止出现一次，即必有结点序列 vj.vs. vs.vk，在路中去掉从 vs 到 vs 的这些边，仍是 vj 到 vk 的一条路， 但此路比原来的路边数要少，如此重复进行下去，必可得到一条从 v j 到 v k 的 不多于 n-1 条边的路

el e2 e3 el e3 v3 3 94 e4 e6 e e6 e7 40 0w540 05 e8 e8 el e2 e3 2 w3 e4 e6 e7 40 0v5 e8 如在图7-2.1中有5个结点。V1到3的一条路为： v1e2v3e3v2e3v3e4v2e6v5e7v3 此路中有6条边，去掉e3有路1e2v3e4v26v5e7v3 有4条边。 y1到v3最短的路为v1e23 二、无向图的连通性： 1、连通 定义7-2.2：在无向图G中，结点u和v之间若存在一条路，则称结 点u和结点v是连通的。 不难证明，结点之间连通性是结点集V上的等价关系，因此对应这个 等价关系，必可对结点集V作出一个划分，把V分成非空子集V1V2

10 如在图 7-2.1 中 有 5 个 结 点 。 v1 到 v3 的 一 条 路 为 ： v1 e2 v3 e3 v2 e3 v3 e4 v2 e6 v5 e7 v3 此路中有 6 条边，去掉 e3 有路 v1 e2 v3 e4 v2 e6 v5 e7 v3 有 4 条边。 v1 到 v3 最短的路为 v1 e2 v3 二、无向图的连通性： 1、连通 定义 7-2.2：在无向图 G 中，结点 u 和 v 之间若存在一条路，则称结 点 u 和结点 v 是连通的。 不难证明，结点之间连通性是结点集 V 上的等价关系，因此对应这个 等价关系，必可对结点集V作出一个划分，把V分成非空子集V 1，V 2