《高等数学》课程教学资源（PPT课件）Ⅱ_第九章 第七节 方向导数与梯度

第八章第七节方向导数与梯度方向导数梯度-三、物理意义机动自录上页下页返回结束

第八章 第七节 一、方向导数 机动 目录 上页 下页 返回 结束 二、梯度 三、物理意义 方向导数与梯度

一、方向导数设l是xoy平面上以点P(xo,yo)为始点的一条射线，é,=(cosα,cosβ)是与l同方向的单位向量x=xo+tcosα射线l的参数方程为(t ≥ 0)(y= yo + tcosβ设函数z = f(x,y)在点 Po(xo,yo)P(x,y)e的某一邻域U(P)内有定义,P(xo + tcosα, yo + tcos β) 为 l上P(xo, yo)另一点，且PU(Po)x考虑lim[PP][PP/->0

o • 0 0 0 P x y ( , ) l e y x • P x y ( , ) 一、方向导数 0 0 0 0 0 0 0 ( , ) ( , ) ( ) ( cos , cos ) ( ) = + +  设函数 在点 的某一邻域 内有定义， 为 上 另一点，且 ． z f x y P x y U P P x t y t l P U P   l 0 0 0 ( , ) (cos ,cos ) 设 是 平面上以点 为始点的一条 射线， 是与 同方向的单位向量. l l xoy P x y e l =   射线l 的参数方程为  0 0 cos ( 0). cos x x t t y y t   = +  = + 0 0 0 考虑 lim . PP z → PP 

z = f(xo + tcosα, yo +tcos β)- f(xo,yo), PPo= t定义函数z=f(x,y)的增量△z与P到P两点间的距离PP=t之比值，当P沿着l趋于P（即t→0+)时,如果此比的极限存在，则称这极限为函数在点P沿方向l的方向导数.记为P(x,y)0zaf或[(Xo,yo)[(xo,yo)alalPo(xo,yo)afAzAz即lim= limX[(xo,yo)PPCal[PP|→>0*t->0+f(xo + tcosα,yo +tcos β)- f(xo,yo)= limt->0

记为 0 0 0 0 ( , ) 0 函数 的增量 与 到 两点间的距离 之比值, 当 沿着 趋于 (即 )时, 如果 此比的极限存在, 则称这极限为 定义 函数在点 沿方向 的方向导数． z f x y z P P PP t P l P P l t + =  = → 0 0 0 ( , ) 0 0 0 0 0 0 0 0 lim lim ( cos , cos ) ( , ) lim + + + → → → = = + + − =     即 x P t y P t f z z t f x t y t t P x l f y P   0 0 0 0 ( , ) ( , ) . x y x y z f l l     或 0 0 0 0  = + + − z f x t y t f x y ( cos , cos ) ( , ),   PP t 0 = o y x • P x y ( , ) • 0 0 0 P x y ( , ) l t

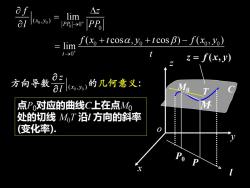
afAzlim1(xo.y0al[PP/->0f(x +tcosα,yo + tcos β) - f(xo,yo)limt→0z = f(x,y)a方向导数的几何意义：al(xo,yo)点Po对应的曲线C上在点MoM处的切线MT沿I方向的斜率(变化率)。0

点P0对应的曲线C上在点M0 处的切线 M0T 沿l 方向的斜率 (变化率). l C P0 T M0 M P o x z y 0 0 ( , ) x y z l 方向导数 的几何意义：   0 0 0 0 0 0 0 0 0 ( , ) 0 lim ( cos , cos ) ( , ) lim + + → →   = + + − =  t x y PP f x t y t f x f z l P y t P   z f x y = ( , )

az注：(1)方向导数就是函数z=f(x,y)[(xo,y0)al在点Po(xo,yo)沿方向1 的变化率。az(2)若偏导数(0,%)存在，取=7 =(1,0),axazaz则存在且等于[(0,%）；反之不然[(xo,yo)axalaz(3) 若偏导数存在，取éj=j=(O,1)(xo.yo)ay0zaz则存在且等于[(xo%)；反之不然I(xo,yo) ayal如z= /x?+ y2在(0,0)点

0 0 ( , ) 0 0 0 (1) ( , ) ( , ) x y z z f x y l P x y l 注： 方向 就是函数 在点 沿方向 数 化 . 导 的变 率  =  0 0 ( , ) (2) 若偏导数 x y 存在，取 l (1,0)， z x e i = =   0 0 0 0 ( , ) ( , ) ; x y x y z l z x 则 存在且等于     反之不然. 0 0 ( , ) 若偏导数 x y 存在，取 el (0,1) ， z j y =  =  0 0 0 0 ( , ) ( , ) ; x y x y z l z y 则 存在且等于     反之不然. 2 2 如 z x y = + 在(0,0) . 点 (3)

若函数z=f(x,J)在点P(xo,y)处可微定理：则函数在该点沿任意方向1的方向导数存在，且有af-(0.Jo) = f,(xo, yo)cosα + f,(xo, yo)cos βal其中α，β为l的方向角证明：由函数f(x,J)在点P可微，得A f = fi(xo, yo)Ax + f,(xo, yo)A y+ o(/(Ax)? +(Ay)?): Ax = tcosα, Ay = tcos β, /(△x) +(Ay)? = tafafat故limcosβcoSα-alaxt-→0+C

定理: 则函数在该点沿任意方向 l 的方向导数存在 , 0 0 ( , ) 0 0 0 0 ( , )cos ( , )cos x y x y f x y f f l   x y   = + 证明: 由函数 f x y ( , ) 2 2 x y 0 0 0 0  =  +  +  +  f f x y x f x y y o x y ( , ) ( , ) ( ( ) ( ) ) 且有 在点 P 可微 , 得 若函数 z f x y = ( , ) 在点 0 0 P x y ( , ) 处可微， 0 lim t f f l t → +   =  故 cos cos . f f x y     = +  

对于二元函数f(x,)，在点P(x,J)处沿方向1(方向角为α,β）的方向导数为af= f.(x,y)cosα + f,(x, y)cos βalx0特别：afaf元一)时,有·当l与x轴同向(α=0,β=2al0xafaf元)时,有·当1与x轴反向（α=元，β=al2ax

对于二元函数 f (x, y), 为,  ) 的方向导数为 在点P(x, y)处沿方向 l (方 ( , )cos ( , )cos x y f f x y f x y l    = +  P l x y o x f l f   =   特别: • 当 l 与 x 轴同向 ( )时,有 2 0,   =  = • 当 l 与 x 轴反向 ( )时,有 2 ,   =   = x f l f   = −   l 向角

例1.求函数z=xe-y花在点点P(1,O)处沿从点P(1,0)到点Q(2,-1)的方向的方向导数解:取方向i= PQ=(1,-1),则é, =(cosα,cosβ) ==azR2y=1二PLreayax(1,0)(1,0)l(1,0)1(1,0)aafz福故所求方向导数为cosβcosα+al0xay

2 y z xe = P(1,0) P(1,0) Q(2, 1) − 例1. 求函数 在点 处沿从点 到点 的方向的方向导数. 解： 取方向l PQ = = − (1, 1)， 则 (cos ,cos ) l e =   1 1 ( , ) 2 2 = − ， 2 (1,0) (1,0) 1; z y e x  = =  2 (1,0) (1,0) 2 2, z y xe y  = =  1 1 1 2 ( ) 2 2 =  +  − 故所求方向导数为 z l  =  2 . 2 = − f f x y     +   cos cos

y=x2-1在点P(2.3)沿曲线例2.求函数z=3x^-朝x增大方向的切线方向的方向导数解：将已知曲线用参数方程表示为X=x122 xN它在点P的切向量为(1,2x)|x=2=(1,4)cos β:cos αOz606x2Va1自结束XH

例2. 求函数 在点P(2, 3)沿曲线 朝 x 增大方向的切线方向的方向导数. 解:将已知曲线用参数方程表示为 2 (1, 2 ) x= 它在点 P 的切向量为 x , 17 1  cos = 17 60 = o x y 2 P    = − = 1 2 y x x x = (1, 4) 17 4 cos  = −1 机动 目录 上页 下页 返回 结束

在点处沿曲线例3求z=1-b=1在此点内法线上的方向导数。(α>0,b>0)6(P51)题：3)X解曲线V1在点P处切线的斜率为0-a则法线的斜率为从而法线的方程为X?O即ba0000机动自录上页返回下页结束

例 3 求       = − + 2 2 2 2 1 b y a x z 在点 ) 2 , 2 ( a b P 处沿曲线 1 2 2 2 2 + = b y a x 在此点内法线上的方向导数。 （P51 题 3） 解 曲线 1 2 2 2 2 + = b y a x 在点P处切线的斜率为 a b y = − 则法线的斜率为 , b a 从而法线的方程为 )，2 ( 2 a x b b a y − = − a b y b a x 2 2 − = − 即 机动 目录 上页 下页 返回 结束 (a  0,b  0)