《高等数学》课程教学资源（PPT课件）Ⅱ_第九章 第二节 偏导数

第八章第二节偏导数偏导数概念及其计算高阶偏导数目录机动上页下页返回结束

第二节 机动 目录 上页 下页 返回 结束 一、 偏导数概念及其计算 二 、高阶偏导数 偏 导 数 第八章

偏导数定义及其计算法引例：研究弦在点xo处的振动速度与加速度，就是将振幅u(x,t)中的x固定于 xo处,求u(xo,t)关于t的一阶导数与二阶导数u(xo,uu(x,t0xoXA反回吉

一、 偏导数定义及其计算法 引例: 研究弦在点 x0 处的振动速度与加速度 , 就是 u(x , t ) 0 o x x u 中的 x 固定于 求 一阶导数与二阶导数. x0 处, ( , ) 0 u x t 关于 t 的 机动 目录 上页 下页 返回 结束 将振幅

设函数 z= f(x,J)在点(xo,Jo）的某邻域内定义1.if(xo + △x, yo) - f(xo, yo)极限limAr-0存在,则称此极限为函数 z= f(x,J)在点（xo,yo）对xOzaf的偏导数，记为2x (xo,yo)0 x(xo, yo)"0 x(xo, yo)fx(xo, yo); fi(xo, yo)f(xo + △x, yo)- f(xo, yo)注意： fx(xo,Jo)= limAx△x-0df(x,yo)x=xodx目录反回结束

定义1. z = f (x, y) 在点 存在, z f (x, y) 在点(x , y ) 对x = 0 0 的偏导数，记为 ( , ) 0 0 x y 的某邻域内 ; ( , ) 0 0 x x y f   x + x 0 0x 则称此极限为函数 极限 设函数 f (x0 ) = ( ) ( ) 0 0 f x + x − f x x 0 lim x→ x ; ( , ) 0 0 x x y z d 0 d x x x y = = ( , ) . 1 0 0 f  x y 机动 目录 上页 下页 返回 结束 x f x x y f x y x  +  − =  → ( , ) ( , ) lim 0 0 0 0 0 ( , ) 0 0 f x y 注意 x :

同样可定义对的偏导数f(xo, yo + △y) - f(xo, yo)Jy(xo,Jo) = lim△y-→0AydXV若函数z=f(x，y)在域D内每一点（x，)处对x或偏导数存在，则该偏导数称为偏导函数，也简称为ozaf记为偏导数, fx(x,y), fi(x,y)oxaxOzaff,(x,y), f2(x,y)ayay0000-F

同样可定义对 y 的偏导数 lim  →0 = y ( , ) 0 0 f x y y 若函数 z = f ( x , y ) 在域 D 内每一点 ( x , y ) 处对 x 则该偏导数称为偏导函数, 也简称为 偏导数 , ( , ) , ( , ) 2 f x y f x y y  ( , ) 0 f x ( , ) 0 − f x y 记为 y + y 0 0 y 机动 目录 上页 下页 返回 结束 或 y 偏导数存在 , , , , y z y f y z    

偏导数的概念可以推广到二元以上的函数例如,三元函数u=f(x，,z)在点(x，,z)处对x的偏导数定义为f(x+△x, y, z)- f(x , y,z)f(x,y,z) = lim△xAx-→0f,(x,y,z2) =?(请自己写出)f.(x, y,z) =?偏导数存在与连续的关系连续一元函数中在某点可导I连续多元函数中在某点偏导数存在结束

例如, 三元函数 u = f (x , y , z) 在点 (x , y , z) 处对 x 的 偏导数的概念可以推广到二元以上的函数 . x x + x f (x, y,z) = ? y f (x, y,z) = ? z x 机动 目录 上页 下页 返回 结束 偏导数定义为 (请自己写出) 偏导数存在与连续的关系 一元函数中在某点可导 连续 多元函数中在某点偏导数存在 连续

函数在某点各偏导数都存在，但在该点不一定连续xy例如，z= f(x,y) =Cd显然fx(0, 0)=f(x, 0)x=0=0dxdf,(0, 0) =f(0, y)V=0=0dy在上节已证f(x，J)在点(0，0)并不连续！0000专方下页返回洁乐

函数在某点各偏导数都存在, 显然 例如,      + = +  = = + 0 , 0 , 0 ( , ) 2 2 2 2 2 2 x y x y x y xy z f x y = 0 = 0 但在该点不一定连续. 上节例 目录 上页 下页 返回 结束 在上节已证 f (x , y) 在点(0 , 0)并不连续!

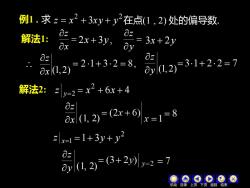
例1.求z=x2+3xy+2在点(1,2)处的偏导数Ozaz解法1：3x +2yaxayOzOzy/(,2)=3.1+ 2.2 = 7=2·1+3.2=8.0x(1,2)解法2：y=2= x2 +6x+ 4az0x/(1, 2) =(2x + 6)=8X=[x=1 =1+3y+ y2azy(1, 2)= (3+ 2y)2=1一目录下页反回结束

例1 . 求 2 2 z = x + 3xy + y 解法1: =   x z x (1,2) z    解法2: x (1, 2) z   在点(1 , 2) 处的偏导数. y (1, 2) z   2x + 3y , =   y z 3x + 2y y (1,2) z   6 4 2 = x + x + x=1 z 2 =1+ 3y + y y=2 z 机动 目录 上页 下页 返回 结束

常数和基本初等函数的导数(x")= uxu-I(C)= 0(a")= a"lna(e")= er(lnx)= 1(log. x) =xlnaX(sinx)= cosx(cosx)'= -sinx(cot x)' = -csc’ x(tanx)'= sec2 x(csc x)'= -cscxcot x(secx)= secx tanx(arccos x)':(arcsin x)' =V/1- xV1-(arctan x)' =(arc cot x)"1+x1+x

常数和基本初等函数的导数 ( )x a  = ln x a a ( )x e  = x e (log ) a x  = 1 x a ln (ln ) x  = 1 x (arcsin ) x  = 2 1 1− x (arccos ) x  = 2 1 1 x − − (arctan ) x  = 2 1 1+ x (arccot ) x  = 2 1 1 x − + (sin ) x  = cos x (cos ) x  = −sin x (tan ) x  = 2 sec x (cot ) x  = 2 −csc x (sec ) x  = sec tan x x (csc ) x  = ( ) C  = 0 ( ) x  =  1 x −  −csc cot x x

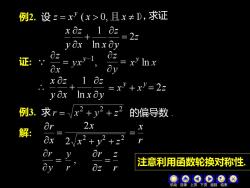
例2.设z=x（x>0,且x±D,求证x Oz1 Oz:2z一yoxIn x OyOzOzvry-证：xln xayaz07-xs=22XyoxIn x Oy例3.求r=的偏导数x~+yOr2Xx解：OxOrd注意利用函数轮换对称性az十目录-下页反回结束

例2. 设 z = x y ( x  0, 且 x  1）， z y z x x z y x 2 ln 1 =   +   证: y z x x z y x   +    ln 1 例3. 求 的偏导数 . 解: =   x r 求证 = 2z 2 2 2 2 x + y + z 2x r x = r z z r =   机动 目录 上页 下页 返回 结束 注意利用函数轮换对称性

第1练习:P71(3),(5),(6)第4题例：P133题5HAU-二-an

机动 目录 上页 下页 返回 结束 练习：P71 第1 （3),(5),(6)第4题。 例：P133 题 5