《高等数学》课程教学资源（PPT课件）Ⅱ_D11_5对坐标的曲面积分

第五节 第十章 对业标的曲面积分 一、有向曲面及曲面元素的投影 二、 对坐标的曲面积分的概念与性质 三、对坐标的曲面积分的计算法 四、两类曲面积分的联系

第五节 一、有向曲面及曲面元素的投影 二、 对坐标的曲面积分的概念与性质 三、对坐标的曲面积分的计算法 四、两类曲面积分的联系 机动 目录 上页 下页 返回 结束 对坐标的曲面积分 第十章

一、有向曲面及曲面元素的投影 双侧曲面 ·曲面分类 曲面分内侧和 单侧曲面 外侧 莫比乌斯带 曲面分左侧和 曲面分上侧和 (单侧曲面的典型) 右侧 下侧 OoO⊙①⑧

一、有向曲面及曲面元素的投影 • 曲面分类 双侧曲面 单侧曲面 莫比乌斯带 曲面分上侧和 下侧 曲面分内侧和 外侧 曲面分左侧和 (单侧曲面的典型) 右侧 机动 目录 上页 下页 返回 结束

•指定了侧的曲面叫有向曲面，其方向用法向量指向 表示： 方向余弦 cosa cos B cosy 封闭曲面 >0为前侧 >0为右侧>0为上侧 外侧 侧的规定 0时 类似可规定 当cosy<0时 当cosy=0时 (AS)(AS) Ooo⊙@⑧

其方向用法向量指向 方向余弦 cos cos  cos > 0 为前侧 0 为右侧 0 为上侧 < 0 为下侧 外侧 内侧 • 设  为有向曲面, ( ) , xy S S (S) x y = 侧的规定 • 指定了侧的曲面叫有向曲面, 表示 : 其面元 在 xoy 面上的投影记为 的面积为 则规定 ( ) ,  xy ( ) , −  xy 0 , 当cos   0时 当cos   0时 当cos   0时 类似可规定 yz zx (S) , (S) 机动 目录 上页 下页 返回 结束

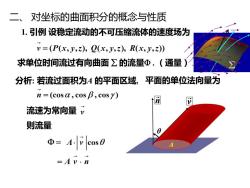
二、 对坐标的曲面积分的概念与性质 1.引例设稳定流动的不可压缩流体的速度场为 v=(P(,y,),(x,z,R(x,y,z) 求单位时间流过有向曲面∑的流量Φ.（通量 分析：若流过面积为A的平面区域，平面的单位法向量为 n =(cosa,cos B,cosy) 流速为常向量， 则流量 Φ=Acos0 =Av·n

二、 对坐标的曲面积分的概念与性质 1. 引例 设稳定流动的不可压缩流体的速度场为 求单位时间流过有向曲面  的流量 . （通量） A  分析: 若流过面积为A 的平面区域, 则流量 平面的单位法向量为 流速为常向量 n v 

对一般的有向曲面Σ，对稳定流动的不可压缩流体的 速度场V=(P(x,y,z),Q(x,y,2),R(x,y,z) 用“分割，近似替代求和，取极限” 进行分析可得Φ=lim∑”·n;AS, →0 i=1 设n=(cosa;,cosB,c0syi),则 2 Φ=1im∑[P(5,n1,5i)cosa+Q(5,7,5i)cosB →01 +R(5,7,5i)C0sY1]AS, =lim∑[P(5,n,5△S,)z+5,ni,5:X△S)zx 2→0 i=1 +R(5i,71,5i)(△S)xy] OaO⊙@☒

 对一般的有向曲面 , 用“分割, 近似替代,求和, 取极限”  = n i 1 0 lim →  = 0 lim → =   = n i 1  P i i i  i ( , , ) cos R i i i i + ( , , ) cos  0 lim → =   = n i 1 Q i i i  i + ( , , ) cos  i S 对稳定流动的不可压缩流体的 速度场 进行分析可得 i n i v i i i v  n S (cos , cos , cos ) i i i i 设 n =     , 则 机动 目录 上页 下页 返回 结束

2.定义.设Σ为光滑的有向曲面，在Σ上定义了一个 向量场A=(P(x,y,z),Q(x,y,),R(x,y,)若对Σ的任 意分割和在局部面元上任意取点，下列极限都存在 Iim∑P(5,7,51AS)z 2→0 i=l +Q(5,7,5i(AS;)zx+R(5,7i,5i)△S)xy] 则称此极限为向量场A在有向曲面上对坐标的曲面积 分，或第二类曲面积分.记作 [Pdyd=+Qd=dx+Rdxdy PQ,R叫做被积函数，Σ叫做积分曲面

设  为光滑的有向曲面, 在  上定义了一个 意分割和在局部面元上任意取点,  = n i 1 i i i i zx + Q( , , )(S ) 分,  Pdy d z + Qd z d x + Rdx dy 记作 P, Q, R 叫做被积函数;  叫做积分曲面. 或第二类曲面积分. 下列极限都存在 向量场 A = (P(x, y,z), Q(x, y,z), R(x, y,z)), 若对 的任 则称此极限为向量场 A 在有向曲面上对坐标的曲面积 2. 定义. 机动 目录 上页 下页 返回 结束

厂Pdydz称为P在有向曲面Σ上对y:的曲面积分 八Odzdx称为Q在有向曲面2上对：，x的曲面积分： 儿Rdxdy称为R在有向曲面Σ上对xy的曲面积分. 引例中，流过有向曲面Σ的流体的流量为 Φ=j八Pdyd:+Qd:dx+Rdx dy 若记正侧的单位法向量为n=(cosa,cos阝，cosy) ds=nds=(dydz,dzdx,dxdy) (称做有向曲面元) 五=(P(x,y,),Q(x,y,),R(x,y,2) 则对坐标的曲面积分也常写成如下向量形式

引例中, 流过有向曲面  的流体的流量为  Pd y d z 称为Q 在有向曲面上对 z, x 的曲面积分;  Rd x d y 称为R 在有向曲面上对 x, y 的曲面积分. 称为P 在有向曲面上对 y, z 的曲面积分;   = Pdy d z + Qd z d x + Rdx dy 若记  正侧的单位法向量为 令 n = ( cos , cos  , cos  ) A = (P(x, y,z),Q(x, y,z), R(x, y,z)) 则对坐标的曲面积分也常写成如下向量形式 机动 目录 上页 下页 返回 结束 d S = n d S = (d yd z, d zd x, d x d y) (称做有向曲面元)

[Pdyd=+edzdx+Rdxdy =八奶不ds=小奶不.ds 3.性质 (1)若Σ=UΣ，且∑，之间无公共内点，则 i= 儿s-主，4as (2)用Σ表示Σ的反向曲面，则 儿fds-k不as 下页返回结束

3. 性质 (1) 若 之间无公共内点, 则 (2) 用 ˉ 表示  的反向曲面, 则  A d S   i A d S  Pd y d z + Q d z d x + Rd x d y  = A nd S  = A d S 机动 目录 上页 下页 返回 结束

三、对坐标的曲面积分的计算法 定理：设光滑曲面∑：z=z(x,y),(x,y)∈Dxy取上侧， R(x,y,z)是∑上的连续函数，则 J八Rx,y)dxdy=j∬R,)dxdy 证：2R(x,)dxdy=im∑R(5h,5△S,)xy 2→0 Σ取上侧，(AS)xy=(△o)xy 5:=z(5,7) =lim∑R(5,n,z(5,n》(△o,)y λ>0i=1 Rdxdy

三、对坐标的曲面积分的计算法 定理: 设光滑曲面 是  上的连续函数, 则  R(x, y,z)d x d y ( , , )  = D x y R x y z(x, y) d x d y 证: 0 lim → =   = n i 1 i x y (S ) i x y ∵ 取上侧 = ( ) , ( , ) i i i  = z   0 lim → =   = n i 1 ( , , ) R i i  i x y ( ) R x y z x,y x y Dx y ( , , ( ))d d  =  R(x, y,z)d x d y 机动 目录 上页 下页 返回 结束 ,取上侧

说明：如果积分曲面Σ取下侧，则 )dxdy=)dxdy ·若∑：x=x(y,2),(y,2)∈Dz,则有 d)dyd= (前正后负) ·若∑：y=y(z,x),(z,x)∈Dx,则有 八(x,y,2)dzdx=∬DQx,(2,x),z)dzdx (右正左负)

• 若 则有  P(x, y,z)d ydz P( , y,z) Dyz  =  x( y,z) d y d z • 若 则有  Q(x, y,z)d z d x ( , , z )  =  Dzx Q x y(z, x) d z d x (前正后负) (右正左负) 说明: 如果积分曲面  取下侧, 则  R(x, y,z)d x d y ( , , )  = − Dx y R x y z(x, y) d x d y 机动 目录 上页 下页 返回 结束