《高等数学》课程教学资源（PPT课件）Ⅱ_第九章 第一节 多元函数的基本概念

第九章 多元菡款微分法 及其寇用 一元函数微分学 推广 多元函数微分学 注意：善于类比，区别异同

推广 第九章 一元函数微分学 多元函数微分学 注意: 善于类比, 区别异同 多元函数微分法 及其应用

第一节 第八章 多元品款的基桡念 区域 二、 多元函数的概念 三、多元函数的极限 四、多元函数的连续性 结

第一节 第八章 一、区域 二、多元函数的概念 三、多元函数的极限 四、多元函数的连续性 机动 目录 上页 下页 返回 结束 多元函数的基本概念

一、 平面点集n维空间 1.平面点集 直角坐标系 平面上的点P 二元有序实数组（化，y) 坐标平面◆→R=R×R={(x,y)川x,y∈R 平面点集：坐标面上具有某种性质P的点的集合 记作：E=(x,y)川（化，y)具有性质P} 例如：平面上以原点为中心、为半径的圆内所有 点的集合为：C={(x,y)川x2+y2<r2} 或C={P‖OPK

一、平面点集 n 维空间 坐标平面 2 R R R x y x y R =  =  {( , ) | , } 平面点集：坐标面上具有某种性质P 的点的集合. 记作： E x y x y = {( , ) | ( , ) } 具有 性质P 例如：平面上以原点为中心、r为半径的圆内所有 点的集合为： 2 2 2 {( , ) | } { || | } C x y x y r C P OP r = +  或 =  1. 平面点集 平面上的点P 二元有序实数组(x, y) 直角坐标系

二、 区域 1.邻域 点集U(P,δ)={PPP<δ，称为点P的δ邻域 例如，在平面上， U(,δ)={《(x,y)V(x-xo)2+(y-o)》2<δ圆邻域) 在空间中， U(B,δ)={《x,y,2V(x-xo)2+(0y-yo)2+(2-zo)2<δ} (球邻域) 说明：若不需要强调邻域半径δ，也可写成U(P) 点P,的去心邻域记为U(P)={P0<PP<δ 返回 结

0 δ  PP0  二、区域 1. 邻域 点集 称为点 P0 的邻域. 例如,在平面上, U ( P0 ,δ ) = (x, y)  (圆邻域) 在空间中, U ( P0 , ) = (x, y,z)  (球邻域) 说明：若不需要强调邻域半径 ,也可写成 ( ). U P0 点 P0 的去心邻域记为 δ PP0  机动 目录 上页 下页 返回 结束

在讨论实际问题中也常使用方邻域，因为方邻域与圆 邻域可以互相包含. 平面上的方邻域为 U(,δ)={(x,y)x-xo<δ，ly-yo<δ} 上页下页返回结束

在讨论实际问题中也常使用方邻域, 平面上的方邻域为 U(P0 ,δ ) = (x, y)  。 P0 因为方邻域与圆 邻域可以互相包含. 机动 目录 上页 下页 返回 结束

2.区域 (1)内点、外点、边界点 设有点集E及一点P: 若存在点P的某邻域U(P)cE, 则称P为E的内点； 若存在点P的某邻域U(P)nE=② 则称P为E的外点， ·若对点P的任一邻域UP)内既含有属于的点也含有 不属于E的点则称P为E的边界点. 显然E的内点必属于E,E的外点必不属于E,E的 边界点可能属于E,也可能不属于E

2. 区域 (1) 内点、外点、边界点 设有点集 E 及一点 P : • 若存在点 P 的某邻域 U(P) E , • 若存在点 P 的某邻域 U(P)∩ E =  , • 若对点 P 的任一邻域 U(P) 内既含有 属于E的点也含有 不属于E E 则称 P 为 E 的内点； 则称 P 为 E 的外点 ; 则称 P 为 E 的边界点 . 机动 目录 上页 下页 返回 结束 的点 , 显然, E 的内点必属于 E , E 的外点必不属于 E , E 的 边界点可能属于 E, 也可能不属于 E

(2)聚点 若对任意给定的δ，点P的去心 邻域U(P,δ)内总有E中的点，则 称P是E的聚点 聚点可以属于E,也可以不属于E(因为聚点可以为 E的边界点) 所有聚点所成的点集称为E的导集 目录 上页下页返回结束

(2) 聚点 若对任意给定的 , 点P 的去心 机动 目录 上页 下页 返回 结束 E 邻域 内总有E 中的点 , 则 称 P 是 E 的聚点. 聚点可以属于 E , 也可以不属于 E (因为聚点可以为 所有聚点所成的点集称为 E 的导集 . E 的边界点 )

(3)开区域及闭区域 ·若点集E的点都是内点，则称E为开集； ·E的边界点的全体称为E的边界，记作E, ·若点集EoE,则称E为闭集； ·若集D中任意两点都可用一完全属于D的折线相连 则称D是连通的； ●连通的开集称为开区域，简称区域； ·开区域连同它的边界一起称为闭区域

D (3) 开区域及闭区域 • 若点集 E 的点都是内点，则称 E 为开集； • 若点集 E E , 则称 E 为闭集； • 若集 D 中任意两点都可用一完全属于 D 的折线相连 , • 开区域连同它的边界一起称为闭区域. 则称 D 是连通的 ; • 连通的开集称为开区域 ,简称区域 ; 机动 目录 上页 下页 返回 结束 。 。 • E 的边界点的全体称为 E 的边界, 记作E ;

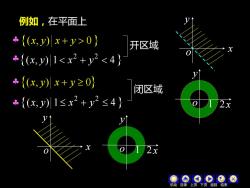
例如，在平面上 {(x,y川x+y>0} 开区域 *{(x,y川1<x2+y2<4} {(x,)x+y≥0} 闭区域 {(x,y)1≤x2+y2≤4) 上页下页返回结束

例如，在平面上 (x, y) x + y  0  ( , ) 1 4  2 2 x y  x + y  (x, y) x + y  0 ( , ) 1 4  2 2 x y  x + y  开区域 闭区域     机动 目录 上页 下页 返回 结束x y o 1 2 x y o x y o x y o 1 2

整个平面是最大的开域 也是最大的闭域； 点集{(x,y)x>}是开集 但非区域. 对点集E,若存在正数r,使得EcU(O,r), 则称E为有界集，否则称为无界集 结

 整个平面  点集 (x, y) x 1 是开集， 是最大的开域 , 也是最大的闭域； 但非区域 . 机动 目录 上页 下页 返回 结束 −1 o 1 x y • 对点集 E , 若存在正数 r , 使得 E U O r  ( , ), 则称 E 为有界集 , 否则称为无界集