《高等数学》课程教学资源（PPT课件）第十章_10_4重积分的应用

第四节 第十章 重积分的应用 立体体积 二、 曲面的面积 三、 物体的质心 四、物体的转动惯量 五、物体的引力 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第四节 一、立体体积 二、曲面的面积 三、物体的质心 四、物体的转动惯量 五、物体的引力 机动 目录 上页 下页 返回 结束 重积分的应用 第十章

1.能用重积分解决的实际问题的特点 所求量是 分布在有界闭域上的整体量 对区域具有可加性 2.用重积分解决问题的方法 ·用微元分析法（元素法） ·从定积分定义出发建立积分式 3.解题要点 画出积分域、选择坐标系、 确定积分序、 定出积分限、计算要简便 HIGH EDUCATION PRESS 机动目 是上页下页返回结束

1. 能用重积分解决的实际问题的特点 所求量是 对区域具有可加性 • 从定积分定义出发 建立积分式 • 用微元分析法 (元素法) 分布在有界闭域上的整体量 3. 解题要点 画出积分域、选择坐标系、确定积分序、 定出积分限、计算要简便 2. 用重积分解决问题的方法 机动 目录 上页 下页 返回 结束

一、立体体积 ·曲顶柱体的顶为连续曲面z=f(x,y),(x,y)∈D, 则其体积为 r=j∬nfx,ard ·占有空间有界域Ω的立体的体积为 =dxdydz HIGH EDUCATION PRESS DeC8 机动目录上页下页返回结束

一、立体体积 • 曲顶柱体的顶为连续曲面 则其体积为  = D V f (x, y)dxdy • 占有空间有界域  的立体的体积为  V = dxdydz 机动 目录 上页 下页 返回 结束

二、 曲面的面积 设光滑曲面S:z=f(x,y),(x,y)∈D 则面积A可看成曲面上各点M(x,y,z) 处小切平面的面积dA无限积累而成. 设它在D上的投影为do,则 应do do =cosy.d4 cosy= V1+2(x,y)+f,2(x,y) dA=1+fs2(x,y)+fy2(x,y)do (称为面积元素) HIGH EDUCATION PRESS 机动目录上页下页返回结束

 M d A z d n 二、曲面的面积 x y z S o 设光滑曲面 则面积 A 可看成曲面上各点 M (x, y,z) 处小切平面的面积 d A 无限积累而成. 设它在 D 上的投影为 d , d = cos  d A 1 ( , ) ( , ) 1 cos 2 2 f x y f x y + x + y  = d 1 ( , ) ( , ) d 2 2 A f x y f x y = + x + y (称为面积元素) 则   M n  d 机动 目录 上页 下页 返回 结束

故有曲面面积公式 4=V1+/2x)+了2(x,)do 即 Ap1++ dxdy 若光滑曲面方程为x=g(y,z),(y,2)∈Dy:,则有 4n1-gaya: HIGH EDUCATION PRESS 机动目录上页下页返回结束

故有曲面面积公式 1 ( , ) ( , ) d 2 2  = + + D x y A f x y f x y x y y z x z A D 1 ( ) ( ) d d 2 2    +   = + 若光滑曲面方程为 ( , ) , ( , ) , Dy z x = g y z y z  则有 Dy z 即 机动 目录 上页 下页 返回 结束

若光滑曲面方程为y=h(:,x),(:,x)∈Dx,则有 4=儿21++8户dd 若光滑曲面方程为隐式F(x,y,z)=0,且F,≠0，则 0z_Fs 0z_Fy F F (x,y)EDxy dxd y F HIGH EDUCATION PRESS 机动目录上页下页返回结束

z x x y z y A 1 ( ) ( ) d d 2 2   +   = +  若光滑曲面方程为 ( , ) , ( , ) , Dz x y = h z x z x  若光滑曲面方程为隐式 则 则有 x y z y z x x y D F F y z F F x z = −    = −   , , ( , )   A = Dx y Dz x z x y z F F F F 2 2 2 + + 且 dx d y 机动 目录 上页 下页 返回 结束

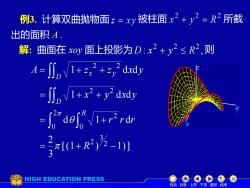
例3.计算双曲抛物面z=xy被柱面x2+y2=R2所截 出的面积A. 解：曲面在xoy面上投影为D:x2+y2≤R2,则 A=∬nN1+2+,2dxdy =∬nV1+x2+y2dxdy -fdordr =31+R2)3-1] HIGH EDUCATION PRESS 机动目录上页下页返回结束

例3. 计算双曲抛物面 被柱面 所截 解: 曲面在 xoy 面上投影为 : , 2 2 2 D x + y  R 则 A z z x y D x y 1 d d 2 2  = + + x y x y D 1 d d 2 2  = + + r r r R d 1 d 0 2 2 0   = +   [(1 ) 1)] 3 2 2 3 2 =  + R − 出的面积 A . 机动 目录 上页 下页 返回 结束

例4.计算半径为α的球的表面积 解：曲面在xoy面上投影为D:x2+y2≤a2,则 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例4. 计算半径为 a 的球的表面积. 机动 目录 上页 下页 返回 结束 解: 曲面在 xoy 面上投影为 2 2 2 D x y a : , +  则

三、物体的质心 设平面有个质点，分别位于(x,y),其质量分别 为m,(k=1,2,n),由力学知，该质点系的质心坐标 ∑xm 为 k= k=1 mk k=1 HIGH EDUCATION PRESS 机动目录上页下页返回结束

三、物体的质心 设平面有n个质点, ( , ) , k k x y 其质量分别 m ( k 1, 2, , n ) , k =  由力学知, 该质点系的质心坐标 , 1 1   = = = n k k n k k k m x m x , 1 1   = = = n k k n k k k m y m y 分别位于 为 为 机动 目录 上页 下页 返回 结束

若物体为占有xoy面上区域D的平面薄片，其面密度 为4(x,),则它的质心坐标为 ∬nx4(x,y)ddy My X= Mx一对x轴的 (xdy M 静矩 (y)dxdy Mx My一对y轴的 静矩 (dxdy M p=常数时，得D的形心坐标 J∬pxdxdy j∬Dddy (A为D的面积 A A HIGH EDUCATION PRESS 机动目录上页下页返回结束

若物体为占有xoy 面上区域 D 的平面薄片, x y x y x x y x y x D D   = ( , )d d ( , )d d   x y x y y x y x y y D D   = ( , )d d ( , )d d    = 常数时, , d d A x x y x D = A y x y y D = d d (A 为 D 的面积) 得D 的形心坐标: 则它的质心坐标为 M M y = M M x = 其面密度 M x M y — 对 x 轴的 静矩 — 对 y 轴的 静矩 机动 目录 上页 下页 返回 结束