《高等数学》课程教学资源（课件讲稿）第六章课件_第六章第2节定积分在几何学上的应用

第六章 第二节 定积分在儿何学上的应用 一、平面图形的面积 二、体积 三、平面曲线的弧长 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第二节 机动 目录 上页 下页 返回 结束 定积分在几何学上的应用 第六章 一、平面图形的面积 二、体积 三、平面曲线的弧长

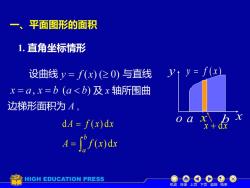
一、平面图形的面积 1.直角坐标情形 设曲线y=f(x)(20)与直线 y↑y=f(x) x=a,x=b(a<b)及x轴所围曲 边梯形面积为A, d4=f(x)dx =()dx HIGH EDUCATION PRESS 机动目录上页下页返回结束

1. 直角坐标情形 设曲线 与直线 及 x 轴所围曲 dA = f ( x) dx o a b x y y = f ( x ) x x + dx A f x x b a ( ) d  = 机动 目录 上页 下页 返回 结束 边梯形面积为 A , 一、平面图形的面积

设曲线y=(x),y=f(x) vy=(x)y=f2(x) 与直线x=a,x=b(a<b) 及x轴所围曲边梯形面积为A axx+dx bx dA=(x)-f(x)dx 4=["f(x)-f2(x)dx HIGH EDUCATION PRESS 机动目 绿上页下页返回结束

1 2 d ( ) ( ) d A f x f x x = − 机动 目录 上页 下页 返回 结束 y o a b x ( ) 2 ( ) y = f x 1 y = f x A f x f x x b a ( ) ( ) d =  1 − 2 x x + d x 设曲线 与直线 及 x 轴所围曲边梯形面积为 A

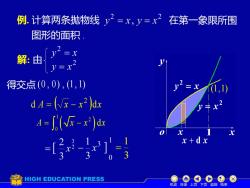
例.计算两条抛物线 y2=x,y=x2在第一象限所围 图形的面积 解由/y y-x 得交点(0,0)，(1,1) d4=（x-x2ax 4=(G-x)a x+dx HIGH EDUCATION PRESS 机动目录上页下页返回结束

例. 计算两条抛物线 在第一象限所围 图形的面积 . x y = x 2 o y 2 y = x x x + d x 解: 由 得交点 (0 , 0) , (1, 1) (1,1) 1 d A ( x x )dx 2 = − 3 1 = 机动 目录 上页 下页 返回 结束 ( ) 1 2 0 A x x x = − d 

例.计算抛物线y2=2x与直线y=x-4所围图形 的面积 解：由 y2=2x 得交点 y=x-4 y2=2x (8.4 (2,-2),(8,4) 为简便计算，选取y作积分变量， 则有 A=2(y+4-2)dy =[5y2+4y-y3]12=18 HIGH EDUCATION PRESS 机动目影 上页下页返回结束

x y 2x 2 = o y y = x − 4 例. 计算抛物线 y 2x 2 = 与直线 的面积 . 解: 由 得交点 (2 , − 2) , (8 , 4) (8 , 4) d A ( y 4 y ) dy 2 2 1 = + − = 18 y = x − 4 所围图形 (2 , − 2) 为简便计算, 选取 y 作积分变量, 则有 y y + d y −  = 4 2 A 机动 目录 上页 下页 返回 结束

例.求椭圆 =1所围图形的面积 62 解： dA=ydx 4-4ydx 利用椭圆的参数方程 oxx+dxa x x=acost l y=bsin t (0≤t≤2π) 应用定积分换元法得 A=4bsin1(-asin）d=4ab sin?tdr =4ab =πab 当a=b时得圆面积公式 HIGH EDUCATION PRESS 机动目录上页下页返回结束

a b o x y x 例. 求椭圆 解: d A = y dx 所围图形的面积 .  = a A y x 0 4 d 利用椭圆的参数方程 (0 2 ) sin cos       = = t y b t x a t 应用定积分换元法得  = 2 0 2 4 sin d  ab t t = 4 ab 2 1  2   =  ab 当 a = b 时得圆面积公式 机动 目录 上页 下页 返回 结束 x + d x

2.极坐标情形 设o(0)eC[a,B],p(0)≥0，求由曲线r=p(0)及 射线0=α，0=B围成的曲边扇形的面积 在区间a,B]上任取小区间[0,0+d0] 则对应该小区间上曲边扇形面积的近似值为 dA-jloPd0 (6 所求曲边扇形的面积为 A0)0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

2. 极坐标情形 求由曲线 及 围成的曲边扇形的面积 . r =  ( )  x  d 在区间 上任取小区间 则对应该小区间上曲边扇形面积的近似值为 ( ) d 2 1 d 2 A = 所求曲边扇形的面积为      ( ) d 2 1 2  A = 机动 目录 上页 下页 返回 结束 

例.计算阿基米德螺线r=a0(a>0)对应0从0变 到2π所围图形面积 2π4 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例. 计算阿基米德螺线 对应  从 0 变 解: x 2 a o  d (  ) d 2 1 2 a  = 2 0 A 2 2 a =       3 3 1  0 2 3 2 3 4 =  a 机动 目录 上页 下页 返回 结束 到 2 所围图形面积

基于阿基米德螺线的风道设计 HIGH EDUCATION PRESS

茶画办工园 白阿基米德螺线样板的制作 我厂生产便携式风力灭火机，其壳体形代是阿基米德螺线，在制作模具时，我们试验 了一种方法，可，（本文共1页）阅读全之2 根院出处1《机械工人冷加工>》2000年0期 机械工人，冷加工 合浅谈阿基米德螺线管式热交换设备的制造 科枝。信息 本文针对阿基米德螺线管的结构、阿基米德螺线管在热交换设.， (本文共1页) 卸读全文>2 权减出处《科技信息》2013年26期 科技信息 阿基米德螺线在盘类机械零件中的应用实例分析 内必精与红年☐ 桂C明 螺旋盘是阿基米德螺线应用于盘类机械零件，在盘内加工等间隔的阿基米德螺线槽 子，在.（本文共2页）阅读全文》 权威出处：《内燃机与配件》2018年16期 内燃机与配件 HIGH EDUCATION PRESS