《高等数学》课程教学资源（课件讲稿）第1章——第2节数列的极限

第一章 第之节款列的款限 一、 数列极限的定义 二、数列极限的性质 等HIGH EDUCATION PRESS 机动目录上页下页返回结束

第一章 二 、数列极限的性质 一、数列极限的定义 第二节 机动 目录 上页 下页 返回 结束 数列的极限

一、数列极限的定义 1、引例 一尺之锤， 日取其半， 万世不竭。 《庄子*天下篇》 HIGH EDUCATION PRESS 机动目录上页下页返回结束

一、数列极限的定义 1、引例 一尺之锤， 日取其半， 万世不竭。 -—《庄子*天下篇》 机动 目录 上页 下页 返回 结束

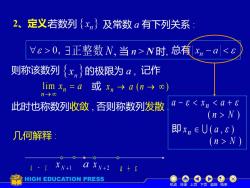
2、定义若数列{x,n}及常数a有下列关系 Vε>0，正整数N,当n>N时，总有xn-aa(n→o） n-→oo 此时也称数列收敛，否则称数列发散 a-8N) 几何解释 即xneU(a,6) (n>N） 00 axN+2 0+8 HIGH EDUCATION PRESS 机动目录上页下页返回结束

2、定义:若数列 及常数 a 有下列关系 : 当 n > N 时, 总有 记作 此时也称数列收敛 , 否则称数列发散 . 几何解释 : a −  a +  a −   x  a +  n ( n  N ) 即 x ( a ,  ) n   ( n  N ) x a n n = →  lim 或 x → a (n →  ) n N +1 x N + 2 x 则称该数列 的极限为 a , 机动 目录 上页 下页 返回 结束

n 例如， 123 234 n+1 Xn= n →1(n→0) n+1 143 n+(-1)-1 收 ’2’3’4 n n 2,4,8，.,2”, xn=2”→0(n→0) 发 1,-1,1,.,(-10+1,. 散 xn=(-1)+l 趋势不定 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例如,  , 1 , , 4 3 , 3 2 , 2 1 n + n +1 = n n xn → 1 ( n →  ) n n x n n 1 ( 1) − + − = → 1 ( n →  ) 2 , 4 , 8 ,  , 2 n ,  n n x = 2 →  ( n →  ) 1 ( 1) + = − n n x 趋势不定 收 敛 发 散 机动 目录 上页 下页 返回 结束

例1.已知x, n+(-l) 证明数列{x,}的极限为1 n 证：xn-1 &>0,欲使xn-1 因此，取N=[],则当m>N时，就有 n+(-1)” n 故 lim=lim n+(1y-1 n-→0 n-→∞ n HIGH EDUCATION PRESS 机动目录上页下页返回结束

例1. 已知 证明数列 的极限为1. 证: xn − 1 = 1 ( 1) − + − n n n    0 , 欲使 即 只要  1 n  因此 , 取 ] , 1 [  N = 则当 n  N 时, 就有 −   + − 1 ( 1) n n n 故 1 ( 1) lim lim = + − = → → n n x n n n n 机动 目录 上页 下页 返回 结束

(-1)n 例2已知xm= (n+2)2' 证明1imxn=0. 证 -l- e∈(0,1)，欲使Ixn-0l-1 n+] w= 取 则当n>N时，就有|xm-0<ε (-1)m 故lim xn三1lim =0 n-∞(n+1)2 GH EDUCATION PRESS

第二节 数列的极限 第一章 函数与极限 例2 已知 证 证明 欲使 只要 取 则当 时, 就有 故 即 0 n x − = ( ) 2 1 n 1 = + 1 n 1   +

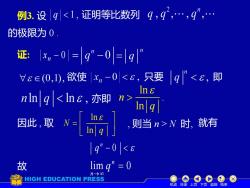
例3.设q n g 因此取[] ,则当n>N时，就有 |q”-0<e 故 limg”=0 n→oo HIGH EDUCATION PRESS 机动目录上页下页返回结束

例3. 设 q  1 , 证明等比数列 证: − 0 n x 欲使 只要 即 亦即 因此 , 取 ln ln N q    =     , 则当 n > N 时, 就有 0 n q −   故 lim 0 n n q →  = ln . ln n q   的极限为 0 . 机动 目录 上页 下页 返回 结束

二、收敛数列的性质 b-ab-a 1.收敛数列的极限唯一 a atb b 证：用反证法.假设lim=a及lim=b,且aN时， n→og -aK经，从而xnN2时，有 n-→00 xn-b 取V=max{N1,N2},则当n>N时，xn满足的不等式 矛盾.故假设不真！因此收敛数列的极限必唯一 HIGH EDUCATION PRESS 机动目 绿上页下页返回结束

 − 2 3a b 2 2 b a n b a x a − − −  −  二、收敛数列的性质 证: 用反证法. 及 且 a  b. 取 因 lim x a , n n = → 故存在 N1 , 从而 2 a b n x +  同理, 因 lim x b , n n = → 故存在 N2 , 使当 n > N2 时, 有 2 a b n x +  1. 收敛数列的极限唯一. 使当 n > N1 时, 假设 2 2 b a n b a x b − − −  −  n a b  x + 2 2 3b−a  从而 2 a b n x +  矛盾. 因此收敛数列的极限必唯一. max , , 则当 n > N 时, 取 N = N1 N2 故假设不真 ! n x 满足的不等式 机动 目录 上页 下页 返回 结束

2.收敛数列一定有界 证：设1imxn=a,取e=1,则3N,当n>N时，有 n-→oo xn-ak1,从而有 xn (xn-a)+als xn-a+a<1+al 取 M=max,xx,1+al 则有 |xnM(n=1,2,.) 由此证明收敛数列必有界 说明：此性质反过来不一定成立.例如， 数列{(-1)+1 虽有界但不收敛 HIGH EDUCATION PRESS 机动目录上页下页返回结束

2. 收敛数列一定有界. 证: 设 取  = 1 , 则  N , 当 n  N 时, 从而有 x a a n  − +  1 + a 取 M = m a x  x1 , x 2 ,  , x N , 1 + a  则有 x  M ( n = 1 , 2 ,  ) . n 由此证明收敛数列必有界. 说明: 此性质反过来不一定成立 . 例如,  1 ( 1 ) + − n 虽有界但不收敛 . x − a  1 , n 有 数列 机动 目录 上页 下页 返回 结束

3.收敛数列的保号性， 若1imxn=a,且a>0 n→o∞ 则归N∈N,当n>N时，有xn>0 若1imxn=a,且aN时，有x,<0 推论.若数列从某项起xn≥0（≤0）且1imxn=a, n-→o0 则a≥0（≤0） HIGH EDUCATION PRESS 机动目 绿上页下页返回结束

3. 收敛数列的保号性. 若 且 时, 有 推论.若数列从某项起 ( 0) ( 0) . 机动 目录 上页 下页 返回 结束 若 且 时, 有