《线性代数》课程教学资源（讲稿B，高教版）第一章 矩阵及其初等变换 1-1 矩阵及其运算

《线性代数》主要内容第一章矩阵及其初等变换第二章行列式第三章n维向量空间第四章特征值与特征向量第五章二次型

《线性代数》主要内容 第一章 矩阵及其初等变换 第二章 行列式 第三章 n维向量空间 第四章 特征值与特征向量 第五章 二次型

第一章矩阵及其初等变换1-1矩阵及其运算1-2高斯消元法与矩阵的初等变换1-3逆矩阵1-4分块矩阵

第一章 矩阵及其初等变换 1-1 矩阵及其运算 1-2 高斯消元法与矩阵的初等变换 1-3 逆矩阵 1-4 分块矩阵

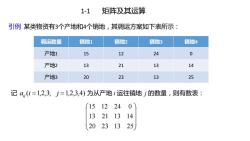
1-1矩阵及其运算引例某类物资有3个产地和4个销地，其调运方案如下表所示：销地1销地2销地3销地4调运数量产地10151224产地221141313产地320231325记a,(i=1,2,3；j=1,2,3,4)为从产地i运往销地j的数量，则有数表：(15012241321131425202313

1-1 矩阵及其运算 引例 某类物资有3个产地和4个销地，其调运方案如下表所示： 调运数量 销地1 销地2 销地3 销地4 产地1 15 12 24 0 产地2 13 21 13 14 产地3 20 23 13 25 记 aij(i 1,2,3; j 1,2,3,4) 为从产地 i 运往销地 j 的数量，则有数表：           20 23 13 25 13 21 13 14 15 12 24 0

一、矩阵的概念定义1由 mxn个数排成的m行 n列的数表(aua12aina21a22a2n::::amlam2am称为一个m 行 n 列的矩阵，记为（aj）mn，或 Amxn。a，称为矩阵A的元素，i为行标，j为列标；元素为实数的矩阵称为实矩阵0(151224比如，矩阵1314211320231325

一、矩阵的概念 定义1 由 mn 个数排成的 m 行 n 列的数表               m m mn n n a a a a a a a a a        1 2 2 1 2 2 2 1 1 1 2 1 称为一个 m 行 n 列的矩阵，记为 (aij) mn ，或 Amn 。 ij a 称为矩阵 A 的元素， i 为行标， j 为列标；元素为实数的矩阵称为实矩阵。 比如，矩阵           20 23 13 25 13 21 13 14 15 12 24 0

aux, +a2x2 +...+ainx, =ba21xj +a2x2 +...+a2nx, = b,再如，研究n元线性方程组的结构amiX+am2X+..+amx,=b,其系数可以组成一个m行n列的矩阵，称A为方程组的系数矩阵，称为方程组的增广矩阵。b,aiiai2aa12ananb2azna22a21a22a21a2nA-A::.:....:..·bm)am2amnamamlam2aml

再如，研究 n 元线性方程组的结构                    m m mn n m n n n n a x a x a x b a x a x a x b a x a x a x b     1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 其系数可以组成一个 行 列的矩阵，称 A 为方程组的系数矩阵， 称 为方程 组的增广矩阵。 m n                m m mn n n a a a a a a a a a A        1 2 2 1 2 2 2 1 1 1 2 1                m m mn m n n b b b a a a a a a a a a A         2 1 1 2 2 1 2 2 2 1 1 1 2 1 A

几个特殊矩阵的概念（1）零矩阵元素全为零的矩阵，记作0(ai ai2 .. an)m=1（2）行矩阵au列矩阵n=1a21.amlaila12aina22a21a2n（3）方阵m=nA=::...an2anlamn)

几个特殊矩阵的概念 （1）零矩阵 （3）方阵 （2）行矩阵 列矩阵 元素全为零的矩阵，记作 O m  n m 1 n 1   a11 a12 a1n                1 21 11 m a a a                 n n n n n n a a a a a a a a a A        1 2 2 1 2 2 2 1 1 1 2 1

几个特殊矩阵的概念00ail00a22（4）对角矩阵A==diag(aj1,a22,...,an).....00a)0100（5）单位矩阵I = diag(1,1,...,1) -00

几个特殊矩阵的概念 （4）对角矩阵 （5）单位矩阵                 an n a a        0 0 0 0 0 0 2 2 1 1 diag( , , , )  a1 1 a2 2  an n                                1 1 1 0 0 1 0 1 0 1 0 0 diag(1,1, ,1)         I 

k（6）数量矩阵kkl = diag(k,k,...,k) -kXY00aiajla12ain（7）上三角矩阵00a21a22a22a2n下三角矩阵............::::00anan2a)ann

（7）上三角矩阵 下三角矩阵 （6）数量矩阵               n n n n a a a a a a        0 0 0 2 2 2 1 1 1 2 1               an an an n a a a        1 2 2 1 2 2 1 1 0 0 0 diag( , , , ) n n k k kI k k k k         

二、 矩阵的线性运算A和B都是mxn矩阵同型矩阵是同型矩阵，且对应元素相等，即α=b,A=(a.), B=(b.)矩阵相等(1 -5)(1N例1设矩阵A=0已知A=B,求x,y,z,B=0￥1343x引例有两种物资从3个产地运往4个销地的调运方案分别记为(150(12122411143201314161321B=1523A=201325(1321,232714如何表示总运量？

二、矩阵的线性运算 同型矩阵 A 和 B 都是 mn 矩阵 矩阵相等 ( ), ( ) A  aij B  bij 是同型矩阵，且对应元素相等，即 aij  bij 例1 设矩阵 已知 ，求                        4 3 0 1 1 , 3 0 1 5 z B x A y A  B x, y,z 引例 有两种物资从3个产地运往4个销地的调运方案分别记为                       13 27 14 21 0 15 23 16 12 11 14 32 , 20 23 13 25 13 21 13 14 15 12 24 0 A B 如何表示总运量？

定义2矩阵的加法设矩阵 A=(aj)mm,B=(by)mn，则 A+B=(a,+b,)mn注：1.只有同型矩阵才能做加法。2.负矩阵-A=(-a,),mx3.矩阵的减法A-B= A+(-B)=(aj-b,)mxnA+B=B+A4.运算规律(A+B)+C= A+(B+C)A+O=AA+(-A)=O

定义2 矩阵的加法 设矩阵 A  (aij) mn , B  (bij) mn ，则 A B  aij bij mn ( ) 注： 1. 只有同型矩阵才能做加法。 2. 负矩阵  A  aij mn ( ) 3. 矩阵的减法 A B  A B  aij bij mn ( ) ( ) 4. 运算规律 A A O A O A A B C A B C A B B A              ( ) ( ) ( )