《线性代数》课程教学资源（讲稿B，高教版）第一章 矩阵及其初等变换 1-4 分块矩阵

1-4分块矩阵对于行数和列数较高的矩阵A，为了简化运算，经常采用分块法，使大矩阵的运算化成小矩阵的运算.具体做法是：将矩阵A用若干条纵线和横线分成许多个小矩阵，每一个小矩阵称为A的子块，以子块为元素的形式上的矩阵称为分块矩阵例如0000012 101012-3A070

1-4 分块矩阵 对于行数和列数较高的矩阵 A, 为了简化运算，经常采用分块法，使大矩阵的 运算化成小矩阵的运算. 具体做法是: 将矩阵 A 用若干条纵线和横线分成许多个小 矩阵，每一个小矩阵称为 A 的子块，以子块为元素的形式上的矩阵称为分块矩阵. 例如            7 3 0 0 0 1 2 3 1 0 1 2          A O I A 21 12               1 2 3 0 0 1 0 1 0 1 0 0          A2 I            7 3 0 0 0 1 2 3 1 0 1 2    A1 A2 A3 A4

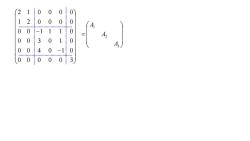
...ECR..0....0)002I002010A0001-1A,=0300...10A,40000-1.......000030

                      0 0 0 0 0 3 0 0 4 0 1 0 0 0 3 0 1 0 0 0 1 1 1 0 1 2 0 0 0 0 2 1 0 0 0 0            3 2 1 A A A

一、分块矩阵的运算1分块矩阵的加法B,B.B=设A与B是同型矩阵，且分块方法相同，A=BB.A..+Bu ... A,+B则A+B=A., + B.LA..+B.2数乘分块矩阵AKkAkA=kAkAAkA

一、分块矩阵的运算 1 分块矩阵的加法                       r r s s r r s s B B B B B A A A A A           1 1 1 1 1 1 1 1 设 A 与 B 是同型矩阵，且分块方法相同， , 则                 r r r s r s s s A B A B A B A B A B      1 1 1 1 1 1 1 1 2 数乘分块矩阵                       r r s s r r s s k A k A k A k A A A A A k A k           1 1 1 1 1 1 1 1

3.分块矩阵的转置设A是一个r×s型分块矩阵，则它的转置是一个s×r型分块矩阵。2AuA=A4/AuA2例如2A=01A21A220002:0101AfA2001则A!4A2110-12

3. 分块矩阵的转置 设 A 是一个 rs 型分块矩阵，则它的转置是一个 sr 型分块矩阵。                       T r s T s T r T T r r s s A A A A A A A A A A           1 1 1 1 1 1 1 1 ,             0 0 2 0 0 1 1 2 1 0 4 1 例如 A          21 22 11 12 A A A A 则          T T T T T A A A A A 1 2 2 2 1 1 2 1                 1 2 0 4 1 2 0 1 0 1 0 0

4.分块矩阵的乘法设矩阵A=(a,）mm,B=(b,）p，对A,B进行分块，其中A的列的分法和B的行的分法相同，则AuBu.A,B.+..A,B...A,B,+..A,Bs.B,..AB=B.BA,B.+.Ar,Bs..A,Bu, +.ABst4A

4. 分块矩阵的乘法                      s s t t r r s s B B B B A A A A AB           1 1 1 1 1 1 1 1 设矩阵 ，对 A, B 进行分块，其中A 的列的分法和 B 的 行的分法相同，则 A  aij mn B  bij np ( ) , ( )                r r s s r t r s s t s s t s s t A B A B A B A B A B A B A B A B          1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

★小结：1.矩阵的分块运算分两步完成，首先，视子块为元素，按矩阵的运算法则作第一步运算，然后，在子块的运算中，再进行实质上的矩车运算2.在对矩阵进行分块时，必须遵守相应运算的前提条件如：相加减的矩阵，需采取完全相同的分块方法；相乘时，左矩阵的列块数必须等于右矩阵的行块数，同时还须保证子块运算时的左子块的列数必须等于右子块的行数

1.矩阵的分块运算分两步完成，首先，视子块为元素， 按矩阵的运算法则作第一步运算，然后，在子块的运算 中，再进行实质上的矩阵运算. 2.在对矩阵进行分块时，必须遵守相应运算的前提条件. 如:相加减的矩阵，需采取完全相同的分块方法；相乘时， 左矩阵的列块数必须等于右矩阵的行块数，同时还须保 证子块运算时的左子块的列数必须等于右子块的行数. ★小结：

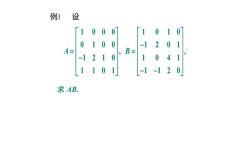
例1 设01020-10B:AE042求 AB

例1 设 1 0 0 0 1 0 1 0 0 1 0 0 1 2 0 1 , , 1 2 1 0 1 0 4 1 1 1 0 1 1 1 2 0 A B                               求 AB

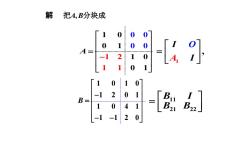
解#把A,B分块成0000001210011福00-20-11Bu1BBB21014122-120-1

解 把A,B分块成1 2 1 1 0 0 1 1 0 0 0 0 1 0 0 1 A               1 , I O A I        1 0 1 0 1 2 0 1 1 0 4 1 1 1 2 0 B                 11 21 22 B I B B       

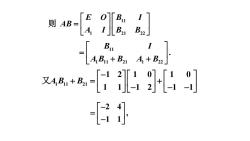
EB0111则 AB=Bz2 JB,LAI2.Blt1A + Bz2.[A,BI + B2140101-12又A,BI + B21 =+12 -1147[-21]L-1

则 11 1 21 22 E O B I AB A I B B              11 1 11 21 1 22 . B I A B B A B          1 11 21 1 2 1 0 1 0 1 1 1 2 1 1 A B B                          又 2 4 , 1 1         

4722=1B11于是AB=A, +B2A,B + B21001141-110343-21[-131?

于是 11 1 11 21 1 22 B I AB A B B A B          1 0 1 0 1 4 0 1 . 2 4 3 3 1 1 3 1                 1 22 1 2 4 1 3 3 , 1 1 2 0 3 1 A B                       