《高等数学》课程教学资源（课件讲稿）第2章 第1讲 导数的概念

高等数学（上册）第2章导数与微分人民邮电出版社POSIS&TELECOMPRESS

高等数学（上册） 第2章 导数与微分

COAORA人邮教育导数思想最早由法国数学家Ferma在研究微积分学的创始人！极值问题中提出英国数学家Newton德国数学家Leibniz导数描述函数变化快慢微分学微分描述函数变化程度都是描述物质运动的工具（从微观上研究函数）

微积分学的创始人: 德国数学家 Leibniz 微分学 导数 描述函数变化快慢 微分 描述函数变化程度 都是描述物质运动的工具(从微观上研究函数) 导数思想最早由法国 数学家 Ferma 在研究 极值问题中提出. 英国数学家 Newton

R人邮教育本章内容V,nvlLaoyu-01导数的概念02函数的求导法则03隐函数及由参数方程确定的函数的求导04函数的微分

01 导数的概念 02 函数的求导法则 03 隐函数及由参数方程确定的函数的求导 04 函数的微分 本 章 内 容

高等数学（上册）第2章导数与微分第1节导数的概念人民邮电出版社POSIS&TELECOMPRESS

高等数学（上册） 第1节 导数的概念 第2章 导数与微分

R人邮教育本讲内容w.ryjiaoyu.co引例0102导数的定义03导数的几何意义04可导与连续的关系

01 引例 02 导数的定义 03 导数的几何意义 04 可导与连续的关系 本 讲 内 容

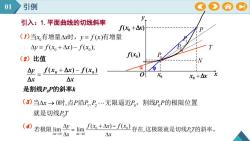
01引例CDAAy引入：1.平面曲线的切线斜率f(x, +Ar)(7)当x有增量△x时，y=f(x)有增量TAy= f(xo +Ax)- f(xo)f(xo)P(2)比值IN&Ayf(x。+Ax)-f(x)xoxoXo +ArAxAr是割线PP的斜率k（3）当△x→O时，点P沿P,P,...无限逼近P，割线P.P的极限位置就是切线PTAyf(+Ax)-f(x)存在,这极限就是切线P,T的斜率。4若极限limlimAxAr->0 AxAr→>0

01 引例 引入：1.平面曲线的切线斜率 （2）比值 x f x x f x x y     ( ) ( ) 0   0  是割线P0P的斜率k   x0 x  ( ) 0 f x ( ) f x0 x   y O x 0 x  （1） 0 0 0 ( ) ( ) ( ); x x y f x y f x x f x        当 有增量 时， 有增量 （3） 1 2 0 0 0 当 0时,点 沿 , 无限逼近 ，割线 的极限位置 就是切线 x P P P P P P PT    （4） 0 0 0 0 0 ( ) ( ) lim lim ,            若极限 存在 这极限就是切线 的斜率。 x x y f x x f x PT x x N P P0 P2 P1 T

2.变速直线运动的瞬时速度COAORA人邮教育设描述质点运动位置的函数为s = s(t)则 t=t。到t=to+△t的平均速度为Ass(to +△t)-s(to)V=△t△t而在 t。时刻的瞬时速度为toto +△tAss(to +△t) - s(to)limv(t.) = limAtAt>0 △tAt->0

2. 变速直线运动的瞬时速度 设描述质点运动位置的函数为 则 到 的平均速度为 而在 时刻的瞬时速度为 s  s(t) 0 t  0 t t t  t0  t 0 0  (   )  ( )     s s t t s t v t t 0 t 0 t0  t t 0 0 0 0 0 ( ) ( ) ( ) lim lim           t  t  s s t t s t v t t t

OOOOR人邮教育Ayf(t。 +△t)- f(to)limk = lim切线斜率变化率问题△tAr→0Ax-0 △x△ss(to +△t) - s(to)limv(t)= lim瞬时速度At->0△tAt-→0 △t两个问题的共性：所求量为函数增量与自变量增量之比的极限

两个问题的共性: 瞬时速度 切线斜率 所求量为函数增量与自变量增量之比的极限 . 变 化 率 问 题 0 0 0 0 ( ) ( ) lim lim           x  x  y f t t f t k x t 0 0 0 0 0 ( ) ( ) ( ) lim lim           t  t  s s t t s t v t t t

R人邮教育本讲内容w.ryjiaoyu.co引例0102导数的定义03导数的几何意义04可导与连续的关系

01 引例 02 导数的定义 03 导数的几何意义 04 可导与连续的关系 本 讲 内 容

02O?导数的定义定义2.1设函数y=f(x）在点xo的某邻域内有定义，当自变量x在xo处有增量△x时,相应函数增量为Ay=f(x+x)-(xo)如果当△x→>0时,极限 lim存在,则称1r->0Ax函数y=f(x）在点xo处可导，并把这个极限值称为函数y=f(x）在点xo处的导数，记作：dfdyf'(x) y'dx!dxAyf(xo +△x)- f(xo)即(2.1)f(x.)=limlimAx->0ArAxAr->0当△x一>0时，这个比值的极限不存在，则称函数在点xo处不可导L

定义2.1 0 0 0 0 d d ( ) , , , , d d x x x x x x f y f x y x x      10 设函数 y  f (x) 在点 x0的某邻域内有定义, 当 当 x  0 时, 这个比值的极限不存在, 则称函数在点 x0处不可导. 自变量x在x0处有增量 x 时, 相应函数增量为 0 y  f(x y  f (x) 在点 x0处的导数, 记作: 如果当x  0时, 极限 li x m 0 存在, 则称 y   x   函数 y  f (x) 在点x0处可导, 0 x)  f (x ). 并把这个极限值称为函数 即 (2.1) 0 0 ( ) lim x y f x x       0 0 0 ( ) ( ) lim x f x x f x   x      02 导数的定义