《高等数学》课程教学资源（课件讲稿）第3章 第5讲 曲线的凹凸性及函数作图

高等数学（上册）第3章微分中值定理与导数的应用第5讲曲线的凹凸性及函数作图人民邮电出版社POSTS&TELECOMPRESS

高等数学（上册） 第5讲 曲线的凹凸性及函数作图 第3章 微分中值定理与导数的应用

R人邮教育本讲内容nw.ryjinoyu.c01曲线的凹凸性与拐点02曲线的渐近线03函数作图

01 曲线的凹凸性与拐点 02 曲线的渐近线 03 函数作图 本 讲 内 容

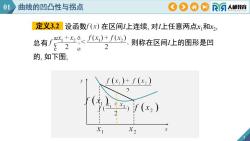
01OOAOR曲线的凹凸性与拐点人邮教育定义3.2设函数f(x）在区间/上连续，对I上任意两点x,和x2f(x)+ f(x2)aexi+x,o总有厂则称在区间I上的图形是凹Ce220的，如下图;f(x,+X2if (x2L2XIX2x

设函数 在区间I上连续, 对I上任意两点x1和x2 定义3.2 , 3 总有 则称在区间I上的图形是凹 的, 如下图; 01 曲线的凹凸性与拐点

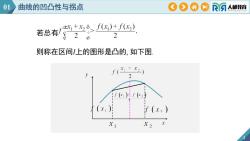
01曲线的凹凸性与拐点COA0RA人邮教育f(x)+ f(x2)ax+x,o若总有ce220则称在区间I上的图形是凸的，如下图F(+x21.2(X)(x,万xif(x)xX1X2

4 若总有 则称在区间I上的图形是凸的, 如下图. 01 曲线的凹凸性与拐点

01C0曲线的凹凸性与拐点RA人邮教育定义3.3连续曲线上凹凸区间的分界点，称为曲线的拐点注:(1)拐点是曲线上的点，应以坐标点(xo,f(x）)表示(2)注意与极值点x=x.表示形式的不同

(1)拐点是曲线上的点, 应以坐标点 表示. (2)注意与极值点 表示形式的不同. 5 定义3.3 连续曲线上凹凸区间的分界点, 称为曲线的拐点. 注: 01 曲线的凹凸性与拐点

01曲线的凹凸性与拐点COAOR人邮教育定理3.12设f(x)在[a,b]上连续,在(a,b)内二阶可导,那么(1)若对"xi (a,b),fx)>0,则f(x)在[a,b]上的图形是凹的;(2)若对"xi(a,b),fx)<0,则f(x)在[a,b]上的图形是凸的

定理3.12 设 在 上连续, 在 内二阶可导,那么 (1)若对 , 则 在 上的图形是凹的; (2)若对 , 则 在 上的图形是凸的. 6 01 曲线的凹凸性与拐点

01COA0曲线的凹凸性与拐点人邮教育PG求函数凹凸区间和拐点的步骤(1)确定函数的定义域(2)求出函数的二阶导数,并解出二阶导数为零的点和二阶导数不存在的点划分区间(3)依次判断每个区间上的二阶导数的符号，利用定理3.12判断每个区间的凹凸性，并进一步求出拐点坐标

求函数凹凸区间和拐点的步骤: (1)确定函数的定义域; (2)求出函数的二阶导数,并解出二阶导数为零的点和二 阶导数不存在的点,划分区间; 判断每个区间的凹凸性,并进一步求出拐点坐标. (3)依次判断每个区间上的二阶导数的符号, 利用定理3.12 7 01 曲线的凹凸性与拐点

01COA0曲线的凹凸性与拐点R人邮教育判定曲线y=lnx的凹凸性例0解定义域为（0,+￥）：(vC所以曲线=lnx在（0,+￥）是凸的

8 判定曲线 的凹凸性. 定义域为 ， ， 例 1 解 01 曲线的凹凸性与拐点 所以曲线 在 是凸的

01曲线的凹凸性与拐点CO0人邮教育R2讨论曲线=sinx在[0,2元]上的凹凸性例香解因为ye=cosx，y=-sinx，所以在(0，元)内，y0，该曲线是凹的

9 ， 例 2 解 01 曲线的凹凸性与拐点 讨论曲线 在 上的凹凸性. 在 内， ，该曲线是凸的； 在 ，该曲线是凹的. 内， 因为 ，所以

01曲线的凹凸性与拐点CO0人邮教育R3判定曲线y=xxarctanx的凹凸性例福x口解定义域为（-￥，+￥），ye=arctanx1+x1- x221+x2- xx2x11Ve(1 +x2)1 + x2(1 + x)2(1 +x2)21 +x所以对xiR，y>0，从而曲线是凹的

10 判定曲线 的凹凸性. 定义域为 , , 所以对 , , 从而曲线是凹的. 例 3 解 01 曲线的凹凸性与拐点