《结构力学》课程授课教案（讲义）第五章 结构的位移计算 5.5 图乘法

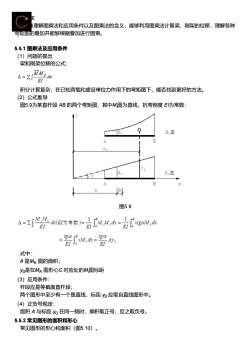
C角理解图乘法和应用条件以及图乘法的含义，能够利用图乘法计算梁、刚架的位移，理解各种弯矩图的叠加并能够根据叠加进行图乘。5.5.1图乘法及应用条件（1）问题的提出梁和刚架位移的公式：MMds=EI积分计算复杂，在已知荷载和虚设单位力作用下的弯矩图下，能否找到更好的方法。(2）公式推导图5.9为某直杆段AB的两个弯矩图，其中M图为直线，抗弯刚度E为常数：y9M图MBxoY:M图MBxx图5.9MMds(EI为常数)=1MMdx=-A=ZxtgaMdEIEIE.tgatgaxM,dx-!AyEIEr式中:A是Mk图的面积yo是在Mk图形心C对应处的M图标距（3）应用条件：杆段应是等截面直杆段：两个图形中至少有一个是直线，标距yo应取自直线图形中。（4）正负号规定：面积A与标距yo在同一侧时，乘积取正号；反之取负号。5.5.2常见图形的面积和形心常见图形的形心和面积（图5.10）

教学要求 正确理解图乘法和应用条件以及图乘法的含义，能够利用图乘法计算梁、刚架的位移，理解各种 弯矩图的叠加并能够根据叠加进行图乘。 5.5.1 图乘法及应用条件 （1）问题的提出 梁和刚架位移的公式： 积分计算复杂，在已知荷载和虚设单位力作用下的弯矩图下，能否找到更好的方法。 （2）公式推导 图5.9为某直杆段 AB 的两个弯矩图，其中Mi图为直线，抗弯刚度 EI为常数： 图5.9 式中： A 是MK 图的面积； y0是在MK 图形心C 对应处的Mi图标距 （3）应用条件： 杆段应是等截面直杆段； 两个图形中至少有一个是直线，标距 y0 应取自直线图形中。 （4）正负号规定： 面积 A 与标距 y0 在同一侧时，乘积取正号；反之取负号。 5.5.2 常见图形的面积和形心 常见图形的形心和面积（图5.10）

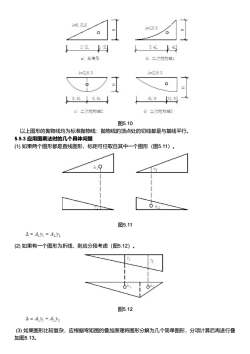
A=0.5LHA=LH/3O2/3L3/4L↓/441a)三角形6）二次抛物线工A=2LH/3A=2LH/30O5L/80.5L0. 5L[3L/8c）二次抛物线2d)二次抛物线3图5.10以上图形的抛物线均为标准抛物线：抛物线的顶点处的切线都是与基线平行。5.5.3应用图乘法时的几个具体问题（1）如果两个图形都是直线图形，标距可任取自其中一个图形（图5.11）：A.912图5.11A=A=A2(2)如果有一个图形为折线，则应分段考虑（图5.12）。力S图5.12A=AN+AY2(3)如果图形比较复杂，应根据弯矩图的叠加原理将图形分解为几个简单图形，分项计算后再进行叠加图5.13

图5.10 以上图形的抛物线均为标准抛物线：抛物线的顶点处的切线都是与基线平行。 5.5.3 应用图乘法时的几个具体问题 (1) 如果两个图形都是直线图形，标距可任取自其中一个图形（图5.11）。 图5.11 (2) 如果有一个图形为折线，则应分段考虑（图5.12）。 图5.12 (3) 如果图形比较复杂，应根据弯矩图的叠加原理将图形分解为几个简单图形，分项计算后再进行叠 加图5.13

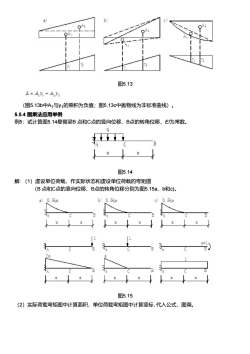
AbO图5.13A=AJ+AY2(图5.13b中A1与y1的乘积为负值；图5.13c中抛物线为非标准曲线）5.5.4图乘法应用举例例5：试计算图5.14悬臂梁B点和C点的竖向位移、B点的转角位移，E/为常数。0图5.14解：（1）虚设单位荷载，作实际状态和虚设单位荷载的弯矩图(B点和C点的竖向位移、B点的转角位移分别为图5.15a、b和c)。0.50ab)0.50a0.50aa)C3图5.15（2）实际荷载弯矩图中计算面积，单位荷载弯矩图中计算竖标，代入公式，图乘

图5.13 （图5.13b中A1与y1的乘积为负值；图5.13c中抛物线为非标准曲线）。 5.5.4 图乘法应用举例 例5：试计算图5.14悬臂梁B 点和C点的竖向位移、B点的转角位移，EI为常数。 图5.14 解: （1）虚设单位荷载，作实际状态和虚设单位荷载的弯矩图 （B 点和C点的竖向位移、B点的转角位移分别为图5.15a、b和c)。 图5.15 （2）实际荷载弯矩图中计算面积，单位荷载弯矩图中计算竖标, 代入公式，图乘

向位移：B点坚向71790-0.5qay=2a=C-68431I7qaA904,=-a=EI6EI24EI4C点竖向位移：13c1gaia.0.5qaA==-α=a-6344ga31Ay9031Ac=a=48EIEI6EIB点转角位移：11a.0.5gcm90iJ=1A=63qa'1Ayqa:.1=0.=SEI6EI6EI例5：试求出图5.16刚架结点B的水平位移和转角，E/为常数。B20oa图5.16解：（1）虚设单位荷载，作实际状态和虚设单位荷载的弯矩图（图5.17a、b、c)

例5：试求出图5.16刚架结点B的水平位移和转角，EI为常数。 图5.16 解: （1）虚设单位荷载，作实际状态和虚设单位荷载的弯矩图（图5.17a、b、c）

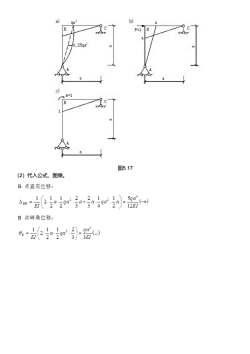
b)2qaP=cL图5.17（2）代入公式，图乘B点竖向位移：172115qa2金21agAR=-ga-a+a.-a3ELcr12EI21B点转角位移：2qai中122aga0=3EI3EI2

图5.17 （ 2）代入公式，图乘