《结构力学》课程授课教案（讲义）第二章 结构的几何构造分析 2.3 平面杆件体系的自由度计算

教学要求掌握实际自由度分析方法了解计算自由度的计算方法2.3.1自由度（1）实际自由度S（即前面讲的"运动自由度"）：体系运动时，可以独立变化的几何参数数目，也就是确定该体系运动所需要的独立参数数目。之所以称之为实际自由度，是为了与下面讲的计算自由度相区别。(2-1)S=（各部件自由度总和a）（非多余约束数总和c)(2）计算自由度W(2-2)W=（各部件自由度总和a）-（全部约束数总和d)由上式可见，计算自由度是由体系部件的自由度和全部约束计算而得，但没有区别非多余约束和多余约束。因此，一般地说，计算自由度不一定就是实际自由度。多余约束数n：等于实际自由度与计算自由度之差，即：(2-3)n=s-W图2-25分析：各部件自由度总和a=2（1个自由点）；约束总数d=4；其中：非多余约束c=2；自由度S=a-c=2-2=0;计算自由度W=a-d=2-4=-2[讨论] :W>0则S>0几何可变W=0则S=n若n=0几何不变W=0则S=n若n>0几何可变W0体系有多余约束,但不一定几何不变。结论：W≤0只是几何不变的必要条件，不是充分条件。2.3.2约束的计算（1）刚片内部多余约束。n=0n=1n=2n=3图2-26刚片内部多余约束[注释]自由端n=0；一根链杆n=1；一个铰n=2；一个刚结n=3;(2）单约束和复约束a.铰结点

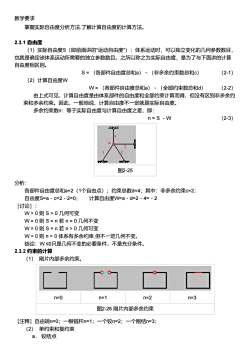
教学要求 掌握实际自由度分析方法,了解计算自由度的计算方法。 2.3.1 自由度 （1）实际自由度S（即前面讲的"运动自由度"）：体系运动时，可以独立变化的几何参数数目， 也就是确定该体系运动所需要的独立参数数目。之所以称之为实际自由度，是为了与下面讲的计算 自由度相区别。 S = （各部件自由度总和a）－（非多余约束数总和c） （2-1） （2）计算自由度W W = （各部件自由度总和a）－（全部约束数总和d） （2-2） 由上式可见，计算自由度是由体系部件的自由度和全部约束计算而得，但没有区别非多余约 束和多余约束。因此，一般地说，计算自由度不一定就是实际自由度。 多余约束数n：等于实际自由度与计算自由度之差，即： n = S －W （2-3） 图2-25 分析： 各部件自由度总和a=2（1个自由点）；约束总数d=4；其中：非多余约束c=2； 自由度S=a－c=2－2=0； 计算自由度W=a－d=2－4=－2 ［讨论］： W > 0 则 S > 0 几何可变 W = 0 则 S = n 若 n = 0 几何不变 W = 0 则 S = n 若 n > 0 几何可变 W 0 体系有多余约束,但不一定几何不变。 结论：W ≤0只是几何不变的必要条件，不是充分条件。 2.3.2 约束的计算 （1） 刚片内部多余约束。 n=0 n=1 n=2 n=3 图2-26 刚片内部多余约束 ［注释］自由端n=0；一根链杆n=1；一个铰n=2；一个刚结n=3； （2） 单约束和复约束 a． 铰结点

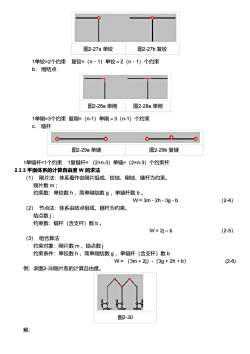
图2-27a单铰图2-27b复铰1单铰=2个约束复铰=（n-1）单铰=2（n-1）个约束b.刚结点图2-28a单刚图2-28a单刚1单刚=3个约束复刚=（n-1）单刚=3（n-1）个约束c.链杆OOOO6图2-29a单链图2-29b复链1单链杆=1个约束1复链杆=（2×n-3）单链=（2×n-3）个约束杆2.3.3平面体系的计算自由度W的求法（1）刚片法：体系看作由刚片组成，铰结、刚结、链杆为约束刚片数m ;约束数：单铰数h，简单刚结数g，单链杆数b。(2-4)W=3m-2h-3g-b(2）节点法：体系由结点组成，链杆为约束。结点数j；约束数：链杆（含支杆）数b。(2-5)W= 2j- b(3）组合算法约束对象：刚片数m，结点数约束条件：单铰数h，简单刚结数g，单链杆（含支杆）数b(2-6)W=(3m +2j) - (3g +2h +b)例：求图2-30刚片系的计算自由度。一图2-30解：

图2-27a 单铰 图2-27b 复铰 1单铰=2个约束 复铰=（n－1）单铰＝2（n－1）个约束 b． 刚结点 图2-28a 单刚 图2-28a 单刚 1单刚=3个约束 复刚=（n-1）单刚＝3（n-1）个约束 c． 链杆 图2-29a 单链 图2-29b 复链 1单链杆=1个约束 1复链杆= （2×n-3）单链=（2×n-3）个约束杆 2.3.3 平面体系的计算自由度 W 的求法 （1） 刚片法：体系看作由刚片组成，铰结、刚结、链杆为约束。 刚片数 m ； 约束数：单铰数 h ，简单刚结数 g ，单链杆数 b 。 W = 3m - 2h - 3g - b （2-4） （2） 节点法：体系由结点组成，链杆为约束。 结点数 j ； 约束数：链杆（含支杆）数 b 。 W = 2j – b （2-5） （3） 组合算法 约束对象：刚片数 m ，结点数 j 约束条件：单铰数 h ，简单刚结数 g ，单链杆（含支杆）数 b W = （3m + 2j）-（3g + 2h + b） (2-6) 例：求图2-30刚片系的计算自由度。 图2-30 解：

方法1方法2方法3方法1：(刚片法)m=7, h=4, g=2, b=6W=3x7-2x4-3x2-6=1方法2：(刚片法）m=5,h=4,g=0,b=6W=3x5-2x4-6=1方法3：（节点法）一一最好j=6, b=11W=2 j -b=2*6-11= 1例：求图2-31刚片系的计算自由度。图2-31解:方法1方法2方法1：（节点法）一—最好j=7, b=14W=2j -b=2*7-14 =0方法2：(刚片法)m=7,h=9, g=0, b=3W=3×7-2x9-3=0例：求图2-32刚片系的计算自由度

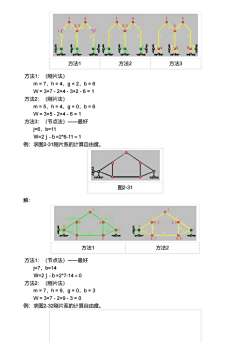
方法1 方法2 方法3 方法1：（刚片法） m = 7，h = 4，g = 2，b = 6 W = 3×7 - 2×4 - 3×2 - 6 = 1 方法2：（刚片法） m = 5，h = 4，g = 0，b = 6 W = 3×5 - 2×4 - 6 = 1 方法3：（节点法）――最好 j=6，b=11 Ｗ=2ｊ-ｂ=2*6-11＝1 例：求图2-31刚片系的计算自由度。 图2-31 解： 方法1 方法2 方法1：（节点法）――最好 j=7，b=14 Ｗ=2ｊ-ｂ=2*7-14＝0 方法2：（刚片法） m = 7，h = 9，g = 0，b = 3 W = 3×7 - 2×9 - 3 = 0 例：求图2-32刚片系的计算自由度

LoQ814TOOT吊OOOTOTTOT3T3图2-32解：方法1：(刚片法)m=1, h=0, g=3, b=4W= 3×1-3x3-4=-10方法2：（节点法）一一最好j=0, b=10W=2j-b=0-10=0

图2-32 解： 方法1：（刚片法） m = 1，h = 0，g = 3，b = 4 W = 3×1- 3×3- 4 = -10 方法2：（节点法）――最好 j=0，b=10 Ｗ=2ｊ-ｂ=0-10＝0