《结构力学》课程教学资源（课件讲稿）第四章 影响线及其应用

2013-6-25第4章影响线教学目标：■了解影响线的概念及其应用；第4章影响线■掌握静力法、机动法作结构的影响线：■掌握利用影响线求移动荷载下结构的最大内力。Influence Lines教学内容：4.1影响线的概念4.2用静力法作结构内力影响线4.3用机动法作梁内力影响线4.3影响线的应用54-1影响线的概念4-1影响线的概念定义：当单位荷载（P-1）在结构上移动时，结构某一指定移动荷载的实例截面中某项内力变化规律的曲线，称为该项内力的影响线。HP=1AItRe目的：解决移动荷载作用下结构的内力计算问题。R.的影响线内容：移动荷载作用下结构内力变化规律；1.0最不利荷载位置一内力极值及相应荷载位置0方法：在各种荷载中抽象出单位荷载（P=1）。24-2静力法作结构内力影响线4-2静力法作结构内力影响线静力法（关键截面内力）R.的影响线P=1 P=1P-1BA.分-7177/71.0ZM,=0=R,a-1x(a-x)=0=R,=1-1.0R的影响线O

2013-6-25 1 第 4 章 影响线 I fl Li Influence Lines 教学目标： 第 4 章 影响线 „ 了解影响线的概念及其应用； „ 掌握静力法、机动法作结构的影响线； „ 掌握利用影响线求移动荷载下结构的最大内力。 教学内容： 4.1 影响线的概念 4.2 用静力法作结构内力影响线 4.3 用机动法作梁内力影响线 4.3 影响线的应用 移动荷载的实例 4-1 影响线的概念 目的：解决移动荷载作用下结构的内力计算问题。 内容：移动荷载作用下结构内力变化规律； 最不利荷载位置—内力极值及相应荷载位置。 方法：在各种荷载中抽象出单位荷载（P =1）。 l 定义：当单位荷载（P=1）在结构上移动时，结构某一指定 截面中某项内力变化规律的曲线，称为该项内力的影响线。 x P=1 4-1 影响线的概念 l RB RB的影响线 1.0 0 A B RA的影响线 P=1 R x A 4-2 静力法作结构内力影响线 a BA A 0 1 01 ( ) x M Ra a x R a ∑ = ⇒ −× − = ⇒ = − 1.0 0 A B a P=1 P=1 静力法（关键截面内力） 4-2 静力法作结构内力影响线 RA的影响线 1.0 0

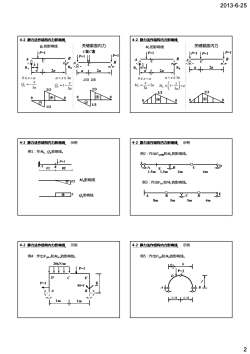
2013-6-254-2静力法作结构内力影响线4-2静力法作结构内力影响线关键截面内力关键截面内力2.的影响线M,的影响线C左C右[P=1P=1/ P=1[P=1 [P=]P=1[P=] -BBABA.TT7:7x1R.A.7172aRaRaRBa2a2020-<x<300≤x<aa<x≤3a0≤x<a-1/3 2/3xO =1-xOc = -Mc=<203a3a2/3a2/3?T?0J1/31/34-2静力法作结构内力影响线，示例4-2静力法作结构内力影响线示例例1：作Mk，Qk影响线。例2：作出FQ右和M,的影响线。↓ P=1X&D22-8_BL-ACE1.5m1.5m3m4m2M影响线12例3：作出F。和M.的影响线。CE19.影响线-&CDB8m5m5m4m4-2静力法作结构内力影响线示例4-2静力法作结构内力影响线示例例4：作出Fon.和Mpa的影响线。例5：作出Fop和M，的影响线。20kN/mP=17DCEP=1M=1 yY770.5lm2

2013-6-25 2 A B QC的影响线 a P=1 2a C x RA RB 4-2 静力法作结构内力影响线 P=1 P=1 C左C右 A B a 2a C 关键截面内力 0 0 2/3 1/3 0 ≤ <x a 3 C x Q a = − ax a < ≤ 3 1 3 C x Q a = − 0 0 -1/3 2/3 2/3 1/3 MC的影响线 A B a P=1 2a C x RA RB 4-2 静力法作结构内力影响线 关键截面内力 P=1 A B a 2a C P P=1 =1 0 0 2/3 0 ≤ x < a 2 3 C x M a a = × ax a < ≤ 3 1 3 C x M a a ⎛ ⎞ = ⎜ ⎟ − × ⎝ ⎠ 0 0 2/3 l/2 l/2 K P=1 A 示例 例1：作MK，QK影响线。 4-2 静力法作结构内力影响线 l/2 Mk影响线 1 Qk影响线 例2：作出FQB右和ME的影响线。 A B C D E 1.5m 1.5m 3m 4m 4-2 静力法作结构内力影响线 示例 例3：作出FQA和MC的影响线。 A B CD E 8m 5m 5m 4m D C E 20kN/m P=1 4-2 静力法作结构内力影响线 示例 例4：作出FQDA和MDA的影响线。 1m 1m A B 1m P=1 M=1 C a b D P=1 4-2 静力法作结构内力影响线 示例 例5：作出FQD和MD的影响线。 f 0.5l 0.5l A B

2013-6-254-2静力法作结构内力影响线，示例4-2静力法作结构内力影响线，示例例6:作YA，M，Mz，Mg，Qc左，Q影响线。例6：作Y，M,，Mz，Mg，Oc左，Q影响线。2B3C4D2B3C4.D1A2mIm,1m,Im,1mm,1m2m1m,1rm2m1m1m1m1mm1m2m1m1mmY影响线M影响线111IM.影响线M,影响线0.501YIA4-2静力法作结构内力影响线，示例4-2静力法作结构内力影响线示例例6:作YA，M，Mz，Mg，Qc左，Q,影响线。例7：作YA，Mc，Mp，Qce影响线。一结点荷载下2B3C41Im,m,Im,1mm,1m 2m 1m ,1mP=12m2.左影响线TT京BASFCDEda0dd/2 / d20.5Q影响线HLS0.54-2静力法作结构内力影响线、示例4-2静力法作结构内力影响线示例杆bc，bC例8：作杆bc，CD，YbccC和dD轴力的影响线。B6d3

2013-6-25 3 YA影响线 例6：作YA ，M1 ，M2 ，MB ， QC左，Q4 影响线。 A 1 23 4 BC D 2m 1m 1m 1m 1m 1m 1m 2m 1m 1m 4-2 静力法作结构内力影响线 示例 M1影响线 1 0.5 1 0 0 0 M2影响线 例6：作YA ，M1 ，M2 ，MB， QC左，Q4 影响线。 4-2 静力法作结构内力影响线 示例 A 1 23 4 BC D 2m 1m 1m 1m 1m 1m 1m 2m 1m 1m 2 MB影响线 1 0 0 0 0 QC左影响线 1 例6：作YA ，M1 ，M2 ，MB ， QC左，Q4 影响线。 4-2 静力法作结构内力影响线 示例 A 1 23 4 BC D 2m 1m 1m 1m 1m 1m 1m 2m 1m 1m 0 0 Q4影响线 1 1 0.5 0.5 0 0 0 0 例7：作YA ，MC，MD， QCE 影响线。—结点荷载下 B P=1 4-2 静力法作结构内力影响线 示例 A B C D E F d d/2 d/2 d d 例8：作杆bc，CD，YbC，cC和dD轴力的影响线。 a b c d e fg h 4-2 静力法作结构内力影响线 示例 A B 6d P=1 CD E F G 杆bc，bC A B 6d P=1 CD E F G a b c d e fg 4-2 静力法作结构内力影响线 示例 A B P=1 CD E F G a b c d e fg Nbc NbC

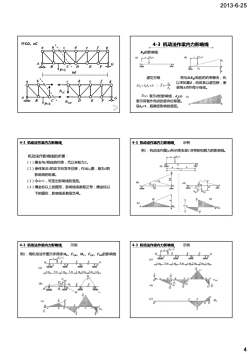
2013-6-25杆CD,cC4-3机动法作梁内力影响线R的影响线(b)(a)F435.P=虚功方程将与Z(Rs)相应的约束撤去，代以未知量Z，给体系以虚位移，使282+F8,=0Z=-5梁绕A点作微小转动。22Z(x)表示z的影响线，,(s）()F表示荷载作用点的竖向位移图。设8,-1，既确定影响线竖距。4-3机动法作梁内力影响线4-3机动法作梁内力影响线示例例1：机动法作图(a)所示简支梁C点弯矩和剪力的影响线。机动法作影响线的步骤：F=（1）撤去与Z相应的约束，代以未知力Z(a)20（2）使体系沿Z的正方向发生位移，作出，图，既为Z的影响线的轮廓。（3）令=1，可定出影响线的竖距。(b)（4）横坐标以上的图形，影响线系数取正号：横坐标以下的图形，影响线系数取负号4-3机动法作架内力影响线示例4-3机动法作梁内力影响线示例yf-lK例2:用机动法作图示多跨梁Mk、FoxMe、FoE、Fk的影响线XB84XCL(a)EAm.3m.lmJm2m/2mjm84XCYD(a)1m.3m.lm_3m.lm2m.2m.jmpFoKt(b)KT(d)e(c)EEELP24

2013-6-25 4 杆CD，cC A B 6d P=1 CD E F G a b c d e fg A B P=1 C D EF G a b d e fg c NcC NCD 4-3 机动法作梁内力影响线 RB的影响线 将与Z(RB)相应的约束撤去，代 以未知量Z，给体系以虚位移，使 梁绕A点作微小转动。 虚功方程 Zδ Z + FPδ P = 0 Z Z δ δ P = − 表示Z的影响线，δp(x) 表示荷载作用点的竖向位移图。 设δZ=1，既确定影响线竖距。 Z (x) 机动法作影响线的步骤： （1）撤去与Z相应的约束，代以未知力Z。 （2）使体系沿Z的正方向发生位移，作出δP图，既为Z的 影响线的轮廓。 4-3 机动法作梁内力影响线 （3）令δz=1，可定出影响线的竖距。 （4）横坐标以上的图形，影响线系数取正号；横坐标以 下的图形，影响线系数取负号。 4-3 机动法作梁内力影响线 示例 例1：机动法作图(a)所示简支梁C点弯矩和剪力的影响线。 例2：用机动法作图示多跨梁MK、FQK、MC、FQE、FRD的影响线 4-3 机动法作梁内力影响线 示例 4-3 机动法作梁内力影响线 示例

2013-6-25示例4-3机动法作梁内力影响线4-4影响线的应用EA4BD1.求实际荷载作用的影响一一集中荷载C(a) jm.3mjm.3m.jm2m2m.jm-求QPPP2+QLeJ2F1(g)RHQc=P-J+Py+P-y4-4影响线的应用4-4影响线的应用，2.求实际荷载作用的影响一一均布荷载3.求荷载的最不利位置求Qc如果荷载移到某一个位置，使某一指定内力达到最大9值（+、-），则此荷载所在位置称为最不利位置。ZACB■一个移动集中荷载IP01mkydx=q·OAB2c=q.dxM影响线①JaJP①AB·影响线面积代数和M,最大值的荷载位置Mkma=Py4-4影响线的应用，示例4-4影响线的应用3.求荷载的最不利位置例：（1）作出Q和M，的影响线：■可动均布荷载（2）图示荷载下的Q右和M10kN/m10kNM,影响线eEYBCFa4m01.5m1.5m3m解：Qn右影响线±b M,=q0A&D1A"EBCM,最大值的荷载位置mM，最小值的荷载位置QB右=10×0+10×(0.5×4×1)=20kN5

2013-6-25 5 4-3 机动法作梁内力影响线 示例 1. 求实际荷载作用的影响——集中荷载 C P1 P2 P3 求QC 4-4 影响线的应用 l a l b QC a b C 1 y 2 y 3 y 1 1 Q P y C = ⋅ 2 2 + P ⋅ y 3 3 + P ⋅ y 2. 求实际荷载作用的影响——均布荷载 dx A B l b Q q C 求QC 4-4 影响线的应用 l a l QC = ∫ ⋅ ⋅ B A C Q q dx y ∫ = B A q ydx AB = q ⋅ω ω AB －影响线面积代数和 y 3. 求荷载的最不利位置 如果荷载移到某一个位置，使某一指定内力达到最大 值（＋、－），则此荷载所在位置称为最不利位置。 4-4 影响线的应用 „ 一个移动集中荷载 P k a b P Mk最大值的荷载位置 Mk,max=Pyk Mk影响线 ya yk yb Mk影响线 ya yk yb q 4-4 影响线的应用 3. 求荷载的最不利位置 „ 可动均布荷载 k a b Mk最大值的荷载位置 Mk最小值的荷载位置 Mk = qω 例：（1）作出QB右和ME的影响线； （2）图示荷载下的QB右和ME； A B C D E 1.5m 1.5m 3m 4m 10kN 10kN/m 4-4 影响线的应用 示例 解：QB右影响线 A B C D E 1 1 0 10 0 10 0.5 4 1 20 ( ) Q kN B右 = ×+ × ×× =

2013-6-254-4影响线的应用示例4-4影响线的应用，示例例2：确定图示多跨连续梁在可动均布荷载作用下M10kN/m10kN的最不利荷载分布。AYDYBC4m.5m1.5m3m解：M影响线M，影响线S0.750-0?M,最大值的荷载位置IDLI-AE8Bm1.5M,最小值的荷载位置Mg=10×0.75+10×(0.5×4×1.5)=37.5kNmOn4-4影响线的应用3.求荷载的最不利位置4-4影响线的应用，PPPP■移动集中力系■移动集中力系SPPP [PM影响线Cdyk+1?dy,dxyyhdye+JNdydxdMc1hJynhysdx=(P+P+.+P)(PI +...Pw)dxM影响线LahMc(x)=Py,+Py,+Px+...+PNnr(P+P,+.+P)"-(P++..P)20badMc(α)=P,dy,+Pedy+P,dy,+.+Prdynh-(P+..P)s0(P+P +...+ P.-)0dMc(x) =dy,(P,+ P, +..+ P)+dy+ (Pa+/+ P++2 +..+ PN)满足上式的P,称作临界荷载，记作P。。41=(P+P++P)=dx-(P+.·Pv)bd临界力位于影响线顶点时的荷载位置称为临界位置。O4-4影响线的应用4-4影响线的应用，■移动集中力系■移动集中力系PPPP[PPPPgbiCb?1Mc影响线yyhJNMc影响线R'+P.、RRJpnhJN[(P+P++P)b.h-(P.P)≥0baa最不利荷载分析步骤：JRLP+R*L(P+P++P..)≤0(1)由临界力判别式确定那些力是临界力；-(Px+..-P)baD(2)计算荷载位于各临界位置时的量值；临界荷载判别式(3)比较得到的量值，得到最大值；临界力位于那一侧，那一侧的等效均布荷载集度就大。(4)最大值发生时的临界位置即是最不利荷载位置。6

2013-6-25 6 解：ME影响线 0 75 4-4 影响线的应用 示例 A B C D E 1.5m 1.5m 3m 4m 10kN 10kN/m A B C D E 0.75 0 ME = × + × ×× = ⋅ 10 0.75 10 0.5 4 1.5 37.5 ( ) kN m 1.5 0 0 例2：确定图示多跨连续梁在可动均布荷载作用下Mk 的最不利荷载分布。 k Mk影响线 4-4 影响线的应用 示例 Mk最大值的荷载位置 Mk最小值的荷载位置 „ 移动集中力系 y1 y2 yk yN a b P1 C P2 Pk PN dx dy1 h dx dyk+1 4-4 影响线的应用 3. 求荷载的最不利位置 MC (x) =P1y1 + P2y2 + Pkyk +.+ PNyN MC影响线 dMC (x) =dy1 (P1+ P2 +.+ Pk)+dyk+1 (Pk+1+ Pk+2 +.+ PN) dMC (x) =P1dy1 + P2dy2 + Pkdyk +.+ PNdyN dx 12 1 ( )( ) k kN h h P P P dx P P dx a b = +++ ⋅− + ⋅ " " + MC影响线 y1 y2 yk yN a b P1 C P2 Pk PN dx dy1 h dx dyk+1 h P P h P P P dM k K N C ( ) ( ) = 1 + 2 +"+ − +1 +" „ 移动集中力系 4-4 影响线的应用 满足上式的Pk称作临界荷载，记作 Pcr 。 临界力位于影响线顶点时的荷载位置称为临界位置。 b P P a P P P dx k K N ( ) ( ) 1 + 2 + + +1 + ( ) ( ) 0 1 + 2 + + − +1 + ≥ b h P P a h P P " Pk K " N ( ) ( ) 0 1 + 2 + + −1 − + ≤ b h P P a h P P " Pk K " N MC影响线 y1 y2 yk yN a b P1 C P2 Pk PN h ( + + + ) ( + ) ≥ 0 h P P h P P P R P RR k L ≥ + „ 移动集中力系 4-4 影响线的应用 临界荷载判别式 临界力位于那一侧，那一侧的等效均布荷载集度就大。 ( ) ( ) 0 1 + 2 + + − +1 + ≥ b P P a P P " Pk K " N ( 1 + 2 + + −1) − ( + ) ≤ 0 b h P P a h P P " Pk K " N a b ≥ b P R a R R k L + ≤ y1 MC影响线 y2 yk yN a b P1 C P2 Pk PN h „ 移动集中力系 4-4 影响线的应用 最不利荷载分析步骤： (1)由临界力判别式确定那些力是临界力； (2)计算荷载位于各临界位置时的量值； (3)比较得到的量值，得到最大值； (4)最大值发生时的临界位置即是最不利荷载位置

2013-6-254-4影响线的应用，：示例4-4影响线的应用，示例例：求图示简支梁C截面弯矩的最不利荷载位置。P=3 Py=7 Pz-2 P,=4. 5kN解：P.Pr-3 Pa-7 Pr-2 Pr-4.5kN是临界力P，是临界力+Y++2+4.5 > RRR'+P..0R*_2+4.5R*+P-3+7>4m 5m 4mmma6b10610DSm6m10mmn10m6mR'2a6S10106baR'+PRR'+P,R判别临界力，判别临界力，RL1P+RR2+4.5拉>bab计算此时的量值，计算此时的量值，a=6b10RLP+REaRLP+R比较得到最大值；比较得到最大值；ba0b4-4影响线的应用，示例4-4影响线的应用，若某量S的影响线为多边形，如图P,和P，是临界力P-3 P-7 Pr=2 Pr=4.5kVPIP+!IPP+P,和P不是临界力mmM= P×3.75+P,×1.25aS影响线α9mm6m10m= 19.375 kN .m3.75M=0.38P+1.88P+3.75P+1.25P1.881.25田RIRR0.38=35.47kN.mPmpJPIIP一Mc.m = 35.47kN.mMc影响线fpp实际计算时，一般并不需验证所有荷载是否为临界力，荷载组左移R,tanα,≤0PJPsPP只考虑那些数值较大、排列密临界荷载判别式荷载组右移ER,tana,≥0集的荷载。4-4影响线的应用小结若某量S的影响线为多边形，如图■影响线概念PpipII PN■作影响线方法：静力法、机动法S影响线a,■影响线的应用确定是否为临界力的荷载情况的判别原则●较多荷载居于影响线正号范围内；。较多荷载居于影响线较大竖标处·排列密集、数值较大荷载位于竖标较大的顶点。27

2013-6-25 7 6m C P4=3 P3=7 P2=2 P1=4. 5kN 4m 4m 5m 10m 10 0 6 2 4.5 = + = + b R a R P R k L > 10 4.5 6 2 = + = b R P R R k L 10 2 4.5 6 7 + = + = b P R a R R k L > MC影响线 判别临界力， 计算此时的量值， 比较得到最大值； b R a R P R k L ≥ + b P R a R R k L + ≤ P3 P2 P1 P2 不是临界力 6m C P4=3 P3=7 P2=2 P1=4. 5kN 4m 4m 5m 10m MC影响线 > < P3 是临界力 10 2 4.5 6 3 7 + = + = + b R a R P R k L 10 7 2 4.5 6 3 + + = + = b R P R R k L 4-4 影响线的应用 示例 MC影响线 < P4 不是临界力 a 6 b 10 10 7 2 6 0 3 + = + = + b R a R P R k L P P3 P2 P1 4 P4 P3 P2 判别临界力， 计算此时的量值， 比较得到最大值； b R a R P R k L ≥ + b P R a R R k L + ≤ 6m C P4=3 P3=7 P2=2 P1=4. 5kN 4m 4m 5m 10m 3 75 kN m M C P P 19 .375 . 3.75 1.25 1 2 1 = = × + × M 0 38P 1 88P 3 75P 1 25P 3 + + + P1和P3 是临界力 P2和P4 不是临界力 4-4 影响线的应用 示例 MC影响线 P2 P1 P4 P3 P2 P1 1.25 1.88 3.75 0.38 kN m MC P P P P 35.47 . 0.38 1 1.88 2 3.75 3 1.25 4 = = + + + MC,max = 35.47kN .m 实际计算时，一般并不需 验证所有荷载是否为临界力， 只考虑那些数值较大、排列密 集的荷载。 若某量S的影响线为多边形，如图 S影响线 P1 P2 Pk PN α1 α 2 α 3 4-4 影响线的应用 P1 P2 Pk PN R1 R2 R3 荷载组左移 ∑ tan ≤ 0 Ri α i 荷载组右移 ∑ tan ≥ 0 Ri α i 临界荷载判别式 4-4 影响线的应用 若某量S的影响线为多边形，如图 S影响线 P1 P2 Pk PN α1 α 2 α 3 确定是否为临界力的荷载情况的判别原则: z 较多荷载居于影响线正号范围内； z 较多荷载居于影响线较大竖标处; z 排列密集、数值较大荷载位于竖标较大的顶点。 小 结 „ 影响线概念 „ 作影响线方法：静力法、机动法 „ 影响线的应用

2013-6-25作业作影响线：4-3刚架、梁》下一章内容4-5a（M0.）结点荷载4-7（RA，2右，M，2G）多跨梁第5章虚功原理与结构位移计算4-9桁架4-13刚架应用：4-15（RA，2.，M.）求反力内力4-17（Qc）不利位置8

2013-6-25 8 4-3 刚架、梁 4-5a（Mc，Qc）结点荷载 4-7（RA，QB右，MF，QG）多跨梁 作影响线： 作 业 4-9 桁架 4-13 刚架 应用： 4-15（RA，Qc，Mc ）求反力内力 4-17（QC）不利位置 ¾ 下一章内容 第 5 章 虚功原理与结构位移计算