《结构力学》课程授课教案（讲义）第六章 力法 6.2 力法的基本概念

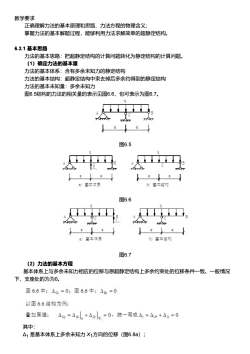
教学要求正确理解力法的基本原理和思路、力法方程的物理含义掌握力法的基本解题过程，能够利用力法求解简单的超静定结构。6.2.1基本思路力法的基本思路：把超静定结构的计算问题转化为静定结构的计算问题。（1）确定力法的基本量力法的基本体系：含有多余未知力的静定结构力法的基本结构：超静定结构中束去掉后多余约得到的静定结构力法的基本未知量：多余未知力图6.5结构的力法的相关量的表示见图6.6，也可表示为图6.7。q图6.5基本体家三本结构6)图6.6基本体系6）基本结构a)图6.7（2）力法的基本方程基本体系上与多余未知力相应的位移与原超静定结构上多余约束处的位移条件一致。一般情况下，支座处的为为0。图6.6中：4=0：图6.6中：45=0以图6.6结构为例：叠加原理：A=+=0，统写成=Ap+=0其中：△1是基本体系上多余未知力X1方向的位移（图6.8a）；

教学要求 正确理解力法的基本原理和思路、力法方程的物理含义； 掌握力法的基本解题过程，能够利用力法求解简单的超静定结构。 6.2.1 基本思路 力法的基本思路：把超静定结构的计算问题转化为静定结构的计算问题。 （1）确定力法的基本量 力法的基本体系：含有多余未知力的静定结构 力法的基本结构：超静定结构中束去掉后多余约得到的静定结构 力法的基本未知量：多余未知力 图6.5结构的力法的相关量的表示见图6.6，也可表示为图6.7。 图6.5 图6.6 图6.7 （2）力法的基本方程 基本体系上与多余未知力相应的位移与原超静定结构上多余约束处的位移条件一致。一般情况 下，支座处的为为0。 其中： Δ1 是基本体系上多余未知力 X1方向的位移（图6.8a）；

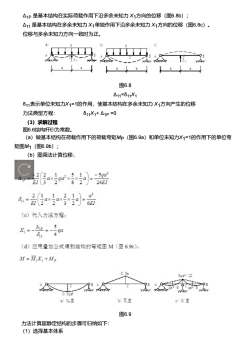
A1P是基本结构在实际荷载作用下沿多余未知力X1方向的位移（图6.8b）；△11是基本结构在多余未知力X1单独作用下沿多余未知力X1方向的位移（图6.8c）。位移与多余未知力方向一致时为正。+F1名图6.8A11=011X1011表示单位未知力X1=1的作用，使基本结构在多余未知力X1方向产生的位移力法典型方程：011X1+ A1P =0(3）求解过程图6.6结构杆EI为常数。（a）做基本结构在荷载作用下的荷载弯矩Mp（图6.9a）和单位未知力X1=1的作用下的单位弯矩图M1（图6.9b）；(b）图乘法计算位移；C-5qa2(251axqaxa8EI24EI3a2(1121o1=-ax=ax-aXEI(26EI232（c）代入力法方程：Au--5X,=490（d）应用叠加公式得到结构的弯矩图M（图6.9c）。M=M,X +M.5g4:/12Oa:O0.50aaME6)X区CME图6.9力法计算超静定结构的步骤可归纳如下：（1）选择基本体系

Δ1P 是基本结构在实际荷载作用下沿多余未知力 X1方向的位移（图6.8b）； Δ11 是基本结构在多余未知力 X1单独作用下沿多余未知力 X1方向的位移（图6.8c）。 位移与多余未知力方向一致时为正。 图6.8 Δ11=δ11X1 δ11表示单位未知力X1=1的作用，使基本结构在多余未知力 X1方向产生的位移 力法典型方程： δ11X1+ Δ1P =0 （3）求解过程 图6.6结构杆EI为常数。 （a）做基本结构在荷载作用下的荷载弯矩MP（图6.9a）和单位未知力X1=1的作用下的单位弯 矩图M1（图6.9b）； （b）图乘法计算位移； 图6.9 力法计算超静定结构的步骤可归纳如下： （1）选择基本体系

确定超静定结构的次数，去掉多余约束，并用相应的约束反力来代替。(2）建立力法方程利用基本体系与原结构在相应约束处的变形条件，建力力法典型方程。（3）计算系数和自由项（4）求多余的未知力(5）作内力图按静定结构，用平衡条件或叠加原理计算结构特殊截面的内力，然后画出内力图。6.2.2力法的基本方程饮超静定结构LE0[OuX,+O,X,+AP=0M=MX+M,X,+M:(4, =010X,+0X,+A2p=0n次超静定[A, =0oX+o,X,++oX +-+oX,+iP=04,=0SX,+oX,+..-+8X+.-+oX,+AP=04,=0.X,+o..X,+.-+oX +..+oX, +A=0M=MX,+M,X,++MX+...+M,X,+M,位移互等定理：j=jij表示单位力X=1在基本结构沿X方向产生的位移，称柔度系数。Aip表示在基本结构实际荷载沿X，方向产生的位移

确定超静定结构的次数，去掉多余约束，并用相应的约束反力来代替。 （2）建立力法方程 利用基本体系与原结构在相应约束处的变形条件，建力力法典型方程。 （3）计算系数和自由项 （4）求多余的未知力 （5）作内力图 按静定结构，用平衡条件或叠加原理计算结构特殊截面的内力，然后画出内力图。 6.2.2 力法的基本方程 位移互等定理：δij=δji δij表示单位力Xj=1在基本结构沿Xi 方向产生的位移，称柔度系数。 ΔiP 表示在基本结构实际荷载沿Xi 方向产生的位移