《结构力学》课程教学资源（课件讲稿）第八章 渐近法

第8章渐进法及其他算法简述教学目标第8章渐进法及其他算法简述■掌握杆件固端弯矩、转动刚度、分配系数和传递系数的物理意义；MethodofSuccessiveApproximations■熟练掌握用力矩分配法计算荷载作用下的连续梁和无侧移刚架；■掌握无剪力分配法与力矩分配法在计算上的异同。■了解近似法■能够计算超静定力的影响线第7章位移法力矩分配法教学内容渐进法无剪力分配法8-1力矩分配法的基本概念选代法8-2/3多结点的力矩分配、对称性逐次逼近一收敛一精确解8-4无剪力分配法8-5力矩分配法与位移法的联合应用特点：8-6近似法①不组成求解方程8-7超静定结构各类解法的比较和合理选用②生动形象，重复步骤，易于手算8-8计算超静定力的影响线1.课程导入8-1力矩分配法的基本概念在结构设计中，结构受力分析具有至关重要的作用。教学要求：■理解转动刚度、分配系数和传递系数的物理意义；■掌握单节点的力矩分配解题的基本过程

1 Method of Successive Approximations 第8章 渐进法及其他算法简述 Method of Successive Approximations 第 8 章 渐进法及其他算法简述 教学目标 „ 掌握杆件固端弯矩、转动刚度、分配系数和传递 系数的物理意义； „ 熟练掌握用力矩分配法计算荷载作用下的连续梁 和无侧移刚架； „ 掌握无剪力分配法与力矩分配法在计算上的异同。 „ 了解近似法 „ 能够计算超静定力的影响线 第 7 章 位移法 8-1 力矩分配法的基本概念 8-2/3 多结点的力矩分配、对称性 8 4 无剪力分配法 教学内容 -4 无剪力分配法 8-5 力矩分配法与位移法的联合应用 8-6 近似法 8-7 超静定结构各类解法的比较和合理选用 8-8 计算超静定力的影响线 逐次逼近 →收敛 →精确解 渐进法 力矩分配法 无剪力分配法 迭代法 逐次逼近 收敛 →精确解 特点： ① 不组成求解方程 ② 生动形象，重复步骤，易于手算 教学要求： 8-1 力矩分配法的基本概念 „ 理解转动刚度、分配系数和传递系数的物 理意义； „ 掌握单节点的力矩分配解题的基本过程。 在结构设计中，结构受力分析具有至关重要的作用。 1. 课程导入

1.课程导入1.课程导入连续梁桥力矩分配法是以位移法为基础，以逐次渐近的方式求无侧移刚架和连续梁杆端弯矩的一种渐进方法。它是1930年由美国的HardyCross教授提出。Cross, Hardy (1930) "Analysis of ContinuousFrames by Distributing Fixed-End Moments".1Proceedings of the American Society of CivilEngineers(ASCE):Pp.919-928.TYY-Y(http://structuremechanics/index1.htm)多跨连续梁2.结点力矩下单结点力矩分配2.2力矩分配法涉及的三个概念例1：若梁线刚度1相同，求梁各杆端弯矩。2.1力矩分配法概念的提出CM例1：若梁线刚度1相同，求梁各杆端弯矩。AcBYCMM（1）转动刚度S(rotationalstfess）BYBlor---C?AMBAMBC是指使杆端发生单位转角时需要施加的力矩。SeHg=-（2）分配系数μ（distributionfactor）回顾位移法2S是指杆件转动刚度与结点连接所有杆件转动刚度和的比值。（3）传递系数C（carry-overfactor）是指当近端有转角时，远端弯矩与近端弯矩的比值。2.2力矩分配法涉及的三个概念2.3结点力矩下单结点力矩分配的解题步骤例2：若梁线刚度1相同，用力矩分配法求梁各杆端弯矩。S值远端支撑情况C值CM=7kNmCABY1.固定4i1/21.结点力矩A4/73/72.分配系数SgA= 4i2.简支40AC&- Snc=3iBY3.分配力矩1/2020434.传递力矩3.滑动WY3M图(kNm)2

2 它是1930年由美国的Hardy Cross教授提出。 力矩分配法是以位移法为基础，以逐次渐近 的方式求无侧移刚架和连续梁杆端弯矩的一种渐 进方法。 1. 课程导入 Cross, Hardy (1930). "Analysis of Continuous Frames by Distributing Fixed-End Moments". Proceedings of the American Society of Civil Engineers (ASCE): pp. 919–928 它是 年由美国的 y 教授提出。 （http://structuremechanics/index1.htm） 连续梁桥 1. 课程导入 多跨连续梁 q 例1：若梁线刚度 i 相同，求梁各杆端弯矩。 A B C M B θB M 2.1 力矩分配法概念的提出 2. 结点力矩下单结点力矩分配 回顾位移法 B B MBA MBC 例1：若梁线刚度 i 相同，求梁各杆端弯矩。 （1）转动刚度S （rotational stiffness） A B C M 2.2 力矩分配法涉及的三个概念 是指使杆端发生单位转角时需要施加的力矩。 （2）分配系数μ （ distribution factor ） Bj Bj B S S μ = ∑ （3）传递系数C （ carry-over factor ） 是指当近端有转角时，远端弯矩与近端弯矩的比值。 是指杆件转动刚度与结点连接所有杆件转动刚度和的比值。 远端支撑情况 S 值 C 值 1. 固定 4i 1/2 2.2 力矩分配法涉及的三个概念 1 S i S 2. 简支 3i 0 3. 滑动 i -1 1 S 1 7 M=7kN·m A B C 例2：若梁线刚度 i 相同，用力矩分配法求梁各杆端弯矩。 2.3 结点力矩下单结点力矩分配的解题步骤 1. 结点力矩 4/7 3/7 2 4 3 0 1/2 0 A B C 2. 分配系数 3. 分配力矩 4. 传递力矩 SBA = 4i SBC = 3i 4 M图（kN·m） A B C 3 2

3.非结点力矩下单结点力矩分配2.3结点力矩下单结点力矩分配的解题步骤计算F,作用下的杆端弯矩。例2：若梁线刚度1相同，用力矩分配法求梁各杆端弯矩。CM=7kN-m4Be.-..8M.MBC""Marc.FAB-口F,1.结点力矩■1.确定结点力矩；（1）在结点B加一个阻止转动的约束，阻止B点的转动。2.分配系数■2.根据转动刚度求分配系数；M,阻止转动的约束3.分配力矩■3.根据分配系数求分配力矩（近端弯矩）：8McM古M&MicO4.传递力矩■4.根据传递系数求传递力矩（远端弯矩）。MLMA图ce(b)M,-M+M-M■约束力矩等于固端弯矩之和。示例例：试用力矩分配法作弯矩图。（2）在结点咖上一个力偶-Mg[200 kN200kNx6m20kN/m放松约束MI&L4FEI6YC--*-MBM-=-150kNmM--M..（3）两种情况叠加，得到实际杆端弯矩。解（1）先在结点B加上约束=150kNm计算固端弯矩和约束力矩。总结■先在刚结点B上加阻止转动的约束，把连续梁0kN20kN/mx(6m)Mic-分为单跨梁，求出杆端弯矩。结点B各杆固端弯矩之8X9-15015000~90和即为约束力矩Mg=-90kNm■去掉约束，求出各杆B端新产生的分配力矩和B）Mg=150kNm-90kNm远端新产生的传递弯矩。0kN-m150kN-=60kNm■叠加各杆端的力矩就得到实际的杆端弯矩。20kN/m（3）叠加得到最后的杆端弯矩9150-901500.5710.429分配系数分配弯矩oc（2）放松结点B1502-90固端弯矩-150M4 = 0.571×(60kNm)在B结点上加一个外力偶分配力矩017.2434.3-25.7 =34.3kNm及传递力矩-60kNm。进行分配和传递。115.Z0Mc =0.429×(60kNm)杆端弯矩167.2115.7转动刚度=-25.7kNmSu=4iSnc=3i167.215.7传递弯矩分配系数14iMA=xMsHBA=Y4i+3i32.117.2kNm3iBeMCR=04i+3iM图（单位kN-m）158.53

3 M=7kN·m A B C 2.3 结点力矩下单结点力矩分配的解题步骤 1. 结点力矩 „ 1. 确定结点力矩； 例2：若梁线刚度 i 相同，用力矩分配法求梁各杆端弯矩。 2. 分配系数 3. 分配力矩 4. 传递力矩 „ 4. 根据传递系数求传递力矩（远端弯矩）。 „ 2. 根据转动刚度求分配系数； „ 3. 根据分配系数求分配力矩（近端弯矩）； 3. 非结点力矩下单结点力矩分配 计算FP作用下的杆端弯矩。 （1）在结点B加 个阻止转动的约束 加一个阻止转动的约束，阻止B点的转动。 FF F MM M M B =+= BA BC BA ■ 约束力矩等于固端弯矩之和。 （2）在结点B加上一个力偶-MB。 （3）两种情况叠加，得到实际杆端弯矩。 总结 ■ 先在刚结点B上加阻止转动的约束，把连续梁 分为单跨梁，求出杆端弯矩。结点B各杆固端弯矩之 和即为约束力矩MB。 ■ 去掉约束，求出各杆B端新产生的分配力矩和 远端新产生的传递弯矩。 ■ 叠加各杆端的力矩就得到实际的杆端弯矩。 例：试用力矩分配法作弯矩图。 解 （1）先在结点B加上约束， 计算固端弯矩和约束力矩 F 200kN 6m 8 150kNm M AB × = − = − F F 150kNm M M BA AB = − = 示例 计算固端弯矩和约束力矩。 150kNm ( )2 F 20 kN/m 6 m 8 90kNm M BC × = − = − 150kNm 90kNm 60kNm M B = − = （2）放松结点B 在B结点上加一个外力偶 -60kNm。进行分配和传递。 转动刚度 分配弯矩 ( ) ( ) ' ' 0.571 60 kNm 34.3 kNm 0.429 60kNm BA BC M M = ×− = − = ×− 4 3 S BA BC = = iS i 转动刚度 = −25.7 kNm 分配系数 4 4 3 3 4 3 BA Bc i i i i i i μ μ = + = + 传递弯矩 ' ' ' 1 2 17.2 kNm 0 AB BA CB M M M = × = − = （3）叠加得到最后的杆端弯矩

8-2/3多结点的力矩分配/对称性小结教学要求：>力矩分配法的基本原理（单结点）三个环节：■理解多结点力矩分配的基本思路：（1）结点力矩；■掌握多节点的力矩分配解题的基本过程。（2）根据分配系数求分配力矩；（3）根据传递系数求传递力矩1.结点力矩下多结点力矩分配的基本思路1.结点力矩下多结点力矩分配的基本思路思考：例1：若梁线刚度1相同，求梁各杆端弯矩。例3：若梁线刚度1相同，求梁各杆端弯矩，M在那步考虑CMCMCMI如何考虑？a)a) AcCDB_CB_限制转动限制转动寿CMCM的约束的约束bA价6)DB_cDB_c.放松约束CMDB_c.-PAB_&b限制转动放松约束等P的约束单结点问题r价d)IADB_-C&放松约束e)CB__Dl示例例1：作连续梁的弯矩图。2.非结点力矩下多结点力矩分配的基本思路20 kN/mJ100kNSc=4ice-1.■每放松一次结点相当进行一FScp=3icp=0.5EF-2CEI-TDA EI-IYB次单结点的分配与传递运算。广6m4m.4m.6m-人Ac=0.667（1）在结点B、C加约束，阻解（1）分配系数Acp= 0.333止结点的转动。0.667SB=4ig=4x（2）固端弯矩（2）去掉结点B的约束qtXMA=-60kNm（结点C仍夹紧）。12M=60kNm0.667（3）重新夹紧结点B，然=0.4B41+ 0.667FplMB-100kNm后去掉结点C的约束，80.6Hse口1+0.667（4）重复（2）和（3），很快达到实际状态。Mce=100kNm4

4 小结 ¾ 力矩分配法的基本原理（单结点） 三个环节： （1）结点力矩； （2）根据分 系数求分 力矩 根据分配系数求分配力矩； （3）根据传递系数求传递力矩。 教学要求： 8-2/3 多结点的力矩分配/对称性 „ 理解多结点力矩分配的基本思路； „ 掌握多节点的力矩分配解题的基本过程。 例1：若梁线刚度 i 相同，求梁各杆端弯矩。 限制转动 的约束 A B C D M b) a) B C D M A 1. 结点力矩下多结点力矩分配的基本思路 b') A B C M C D 单结点问题 1. 结点力矩下多结点力矩分配的基本思路 例3：若梁线刚度 i 相同，求梁各杆端弯矩。 限制转动 的约束 A B C D M b) a) B C D M A 等 价 M 思考： M在那步考虑， 如何考虑？ A B C D c) 放松约束 A B C D e) 放松约束 A B C D d) 限制转动 放松约束 等 的约束 价 （1）在结点B、C加约束，阻 止结点的转动。 ■ 每放松一次结点相当进行一 次单结点的分配与传递运算。 2. 非结点力矩下多结点力矩分配的基本思路 （2）去掉结点B的约束 （结点C仍夹紧）。 （3）重新夹紧结点B ，然 后去掉结点C的约束。 （4）重复（2）和（3），很快达到实际状态。 例1：作连续梁的弯矩图。 解 1 S i 4 4 0 66 4 1 3 0.5 CB CB CD CD S i S i = = = = 0.667 0.333 CB CD μ μ = （1）分配系数 = 示例 1 44 0.667 6 2 44 1 8 BA BA BC BC S i S i = =× = = =× = 0.667 0.4 1 0.667 1 0.6 1 0.667 BA Bc μ μ = = + = = + 2 F F F P F 60kNm 12 60kNm 100 kNm 8 100kNm AB BA BC CB ql M M F l M M =− =− = =− =− = （2）固端弯矩

例2：作图示刚架的弯矩图、剪力图和轴力图。20 kN/m1100 kNCEDc=0.445AE-E/w2ScB=420kN/n6m/4ml4m/6mμcp = 0.333ScF=24107（3）放松结点CD.400D.6000.6670.333μcr=0.222分配系数Scp=3D3a31国端考起6060-5-100100-33.4--66.7-33.3（4）锁住结点C（2）固端弯矩放松结点Bg7.3-27.3-~14.74mMEA=40kNm2.2+8（5）进行第二个循环0.7+1.50.7解（1）转动刚度和分配系数qtMEC=41.3|41.3（6）进行第三个循环-41.7kNm杆编弯短-43.692.6-92.6El=112Mc=41.7kNm（7）将固端弯矩、分配μg,= 0.3SsA=343.6.41.3弯矩、传递弯矩相加。p&DSsE=3μBc = 0.4（3）力矩分配WC23.521.988（8）根据杆端弯矩画M图μB=0.3Snc =4按C、B顺序分配两轮。M图（单位KN:m）CBCFCDBABEBC0.4450.2220.3330.30.30.4D8（4）内力图8A40n29.由杆端弯矩作弯矩图：3.33.303n1.00.50.5由杆件的平衡条件作剪力图；0.150.15 ~0.25424.29.814.6由结点的平衡条件作轴力图。3.5546.43.43FCF。图（单位kN）43.4.24(单位kN·m)-40BLAaBWC9.88.2.3.A26.81.7■放松结点的顺序不影响最后的结果。4.915105F图（单位KN)49.2■先放松结点约束力矩大的结点，收敛速度快。M图（单位kN-m）3.对称性应用例3：作图示结构的M图。解（1）锁住B、C两点1SOkNEI=常数T.M=-50kNm&■作用在对称结构上的任意荷载，都可分解为对称a5mWimt（2）放松C结点荷载和反对称荷载。ADSca-4E1/5Mca =1·对称荷载作用下，弯矩图和轴力图是对称，剪力C-50Acp=0Scp =0图是反对称的。502分配、传递。50 5020.8 20.8■反对称荷载作用下，弯矩图和轴力图是反对称，（3）C结点不再锁住。(单位KN-m)放松结点Bt剪力图是对称的。Su-3EI/148. = 5/6■利用这些性质，在对称结构中可取半边结构进行SBc=3E1/5μsc = 1/6计算。只分配、不传递。（4）画弯矩图20.8M图（单位kN-m)5

5 （3）放松结点C （4）锁住结点C， 放松结点B （5）进行第二个循环 （6）进行第三个循环 （7）将固端弯矩、分配 弯矩、传递弯矩相加。 （8）根据杆端弯矩画M图 例2：作图示刚架的弯矩图、剪力图和轴力图。 4 2 3 CB CF CD S S S = = = 0.445 0.333 0.222 CB CD CF μ μ μ = = = （2）固端弯矩2 40kN F ql M 解（1）转动刚度和分配系数 3 3 4 BA BE BC S S S = = = 0.3 0.4 0.3 BA BC BE μ μ μ = = = 2 40kNm 8 41.7 kNm 12 41.7 kNm F BA F BC F CB q M ql M M = = =− =− = EI0=1 （3）力矩分配 按C、B顺序分配两轮。 ■ 放松结点的顺序不影响最后的结果。 ■ 先放松结点约束力矩大的结点，收敛速度快。 （4）内力图 由杆端弯矩作弯矩图； 由杆件的平衡条件作剪力图； 由结点的平衡条件作轴力图。 例3：作图示结构的M图。 解 （1）锁住B、C两点 4 /5 0 CB CD S EI S = = 1 0 CB CD μ μ = = F MCD = −50kNm （2）放松C结点 （3）C结点不再锁住。 放松结点B 3 /1 3 /5 BA BC S EI S EI = = 5 6 1 6 BA BC μ μ = = 只分配、不传递。 （4）画弯矩图 分配、传递。 ■ 作用在对称结构上的任意荷载，都可分解为对称 荷载和反对称荷载。 ■ 对称荷载作用下，弯矩图和轴力图是对称，剪力 图是反对称的 3. 对称性应用 。 ■ 反对称荷载作用下，弯矩图和轴力图是反对称， 剪力图是对称的。 ■ 利用这些性质，在对称结构中可取半边结构进行 计算

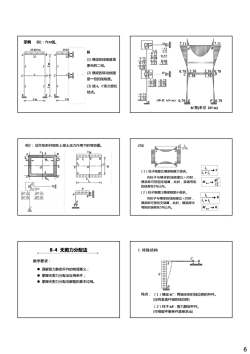
示例例1：作M图。7.117.11GB0蓝20 kN/m20kl解-0.372/5-21(1)横梁的线刚度是-9.%原来的二倍。0.78A2.362.36月0.78(2)横梁的转动刚度HB1.3818CT.38是一倍的线刚度。(3）按A、C依次放松结点。39（单位kN-m）0.79EF0.79BM图(单位kN·m)例2：试作矩形衬在上部土压力作用下的弯矩图。讨论+49.（1）柱子刚度比横梁刚度大很多。i,+i17当柱子与横梁的线刚度比>20时91横梁即可按固定端算，此时，梁端弯矩M12的误差在5%以内。Pe（2）柱子刚度比横梁刚度小很多。如市a120-209t70当柱子与横梁的线刚度比<20时，i+i横梁即可按铰支端算，此时，横梁跨中YY弯矩的误差在5%以内。M→08-4无剪力分配法1.特殊结构教学要求：■理解剪力静定杆件的物理意义：■掌握无剪力分配法应用条件：■掌握无剪力分配法解题的基本过程。B特点：（1）横梁AC：两端无相对线位移的杆件。(没有垂直杆轴的线位移)（2）柱子AB：剪力静定杆件。(可根据平衡条件直接求出）6

6 例1：作M图。 解 (1) 横梁的线刚度是 原来的二倍。 (2) 横梁的转动刚度 示例 ( ) 是一倍的线刚度。 (3) 按A、C依次放松 结点。 例2： 试作矩形衬砌在上部土压力作用下的弯矩图。 讨论 （1）柱子刚度比横梁刚度大很多。 2 1 2 1 i i i → + 当柱子与横梁的线刚度比>20时 2 1 12 BA ql M → 当柱子与横梁的线刚度比>20时， 横梁即可按固定端算，此时，梁端弯矩 的误差在5%以内。 （2）柱子刚度比横梁刚度小很多。 2 1 2 0 i i i → + 0 M BA → 当柱子与横梁的线刚度比<20时， 横梁即可按铰支端算，此时，横梁跨中 弯矩的误差在5%以内。 教学要求： 8-4 无剪力分配法 „ 理解剪力静定杆件的物理意义； „ 掌握无剪力分配法应用条件； „ 掌握无剪力分配法解题的基本过程。 1.特殊结构 （1）横梁AC：两端无相对线位移的杆件。 (没有垂直杆轴的线位移) （2）柱子AB：剪力静定杆件。 (可根据平衡条件直接求出) 特点：

解决办法MA锁住结点（只阻止结点的角位移，不阻止线位移）结点变形：有转角、有侧移XeNV杆件受力：剪力为零，弯矩为常数A+Fo=0109F若杆端发生转角6A，则上边滑动下边固定Mn=inos,Ma.=-ineEBBSAn=inCAB= -10放松结点时，刚架中静定剪力杆都是在零剪力的条件下按该端滑动、另端固定的杆件进行计算。得到分配弯矩和传递弯矩的，故称无剪力分配法。3.剪力静定杆件的固端弯矩2.无剪力分配法的应用条件无剪力分配法计算刚架的步骤与力矩分配法相同，两类杆件FD但固端弯矩、转动刚度和分配系数的求法不同横梁：锁住结点（只阻止结点的角位移，不阻止线位移），F,cl两端无相对线位移的杆件。2F,FB8柱子：3F,剪力静定杆件。上边滑动E8B下边固定1/无剪力分配法的应用条件（1）根据静力条件求出杆端剪力刚架中只包含杆端无相对线位移杆件和剪力静定杆件。（2）将剪力看成杆端荷载，按该端滑动、另端固定的杆件计算示例例1：试作刚架的弯矩图。4.零剪力杆件的转动刚度和传递系数I5kNc解（1）固端弯矩放松结点相当于在结点处施加一反向的约力矩i,=43MEC=F,I= -3.75kNm16$M=.gl?=-2.67kNm月1-3结点变形：有转角、有侧移6.g2杆件受力：剪力为零，弯矩为常数MER-=-5.33kNmLFo=o3L2m2m若杆端发生转角6A，则（2）转动刚度和分配系数Mn=isOa,Maa=-iano,μBc = 4/5Sac = 3, =12SAB-iACAB = -1SBA= 1/5CBu=-1Sn. =i, =37

7 锁住结点（只阻止结点的角位移，不阻止线位移）。 解决办法 上边滑动 下边固定 按该端滑动、另端固定的杆件进行计算。 结点变形：有转角、有侧移 杆件受力：剪力为零，弯矩为常数 若杆端发生转角θA，则 , Mi M i AB AB A BA AB A = θ = − θ S AB AB = i 1 CAB = − 放松结点时，刚架中静定剪力杆都是在零剪力的条件下 ，得到分配弯矩和传递弯矩的，故称无剪力分配法。 两类杆件 横梁： 两端无相对线位移 的杆件。 2.无剪力分配法的应用条件 柱子： 剪力静定杆件。 无剪力分配法的应用条件 刚架中只包含杆端无相对线位移杆件和剪力静定杆件。 无剪力分配法计算刚架的步骤与力矩分配法相同， 但固端弯矩、转动刚度和分配系数的求法不同 锁住结点（只阻止结点的角位移，不阻止线位移）。 3. 剪力静定杆件的固端弯矩 上边滑动 下边固定 （1）根据静力条件求出杆端剪力； （2）将剪力看成杆端荷载，按该端滑动、另端固定的杆件计算。 放松结点相当于在结点处施加一反向的约束力矩。 结点变形：有转角、有侧移 4.零剪力杆件的转动刚度和传递系数 杆件受力：剪力为零，弯矩为常数 若杆端发生转角θA，则 , Mi M i AB AB A BA AB A = =− θ θ S AB AB = i 1 CAB = − 例1： 试作刚架的弯矩图。 解 （1）固端弯矩 F P 2 F 3 - = -3.75kNm 16 - = -2.67 kNm 6 BC BA M Fl ql M = = 示例 2 F - = -5.33kNm 3 AB ql M = （2）转动刚度和分配系数 1 2 3 = 12 = 3 BC BA S i S i = = 4 5 1 5 BC SBA μ = = 1 CBA = −

SINAO例2：作图示刚架的弯矩图OO（1）固端弯矩解BABC17kN8?11/54/5CMA=MA×4kN×3.3mB1.392ApO1.39翻?-2.67-3.75=-6.6kNm1.285.14Ic1.39-1.39Mc=Me×(4+8.5)kNx3.6m5.70=-22.5kNm4ND5.33O（2）分配系数-1.28M图（单位kN-m）6.61(单位kNm)s3.5/170.5=0.0206S.=iu.-3.583KN256.61μsc = 5/170.5 = 0.0293SBc =ic =5?4r=162/170.5=0.9501Ssp=3i=1627.057.058-5力矩分配法与位移法的联合应用A>D目-教学要求：27.79T■理解联合应用的方法；豆月B21.64E21.64■掌握力矩分配法与位移法的联合求解结构。6.156.150.8527.65丰27.79M图（单位kN·m）-233623.3623.36(单位kN-m)1.力矩分配法与位移法联合应用的计算方法示例例1：求刚架内力。解m20kN/m（1）基本体系：取DD点水平线位移作为基本8st未知量基本体系（2）位移法方程k.A,+F,=0（3）求系数和自由项C0.436P0.594^作4,=1时的弯矩图0.48（1）基本体系只取线位移作基本未知量。D-1因为侧移是已知的，（2）位移法方程kA,+Fp=0可用力矩分配法计算。.96=0.443（3）求系数和自由项，解方程用力矩分配法求K= 0.594grc~0.1510.467(4)M = M,A,+M,M,图8

8 例2：作图示刚架的弯矩图 解 （1）固端弯矩 F F F F 1 4 kN 3.3 m 2 = 6.6 kN m 1 (4 8.5)kN 3.6m 2 AB BA BC CB M M M M = =− × × − = =− × + × 2 = 22.5kN m BC CB − 3.5 5 3 162 BA BA BC BC BE BE S i S i S i = = = = = = 3.5 170.5 0.0206 5 170.5 0.0293 162 170.5 0.9501 BA BC BE μ μ μ = = = = = = （2）分配系数 教学要求： 8-5 力矩分配法与位移法的联合应用 „ 理解联合应用的方法； „ 掌握力矩分配法与位移法的联合求解结构。 1. 力矩分配法与位移法联合应用的计算方法 （1）基本体系 只取线位移作基本未知量。 （2）位移法方程 11 1 1P k F Δ+ = 0 （3）求系数和自由项，解方程 用力矩分配法求 （4） MM M = Δ+ 11 P 例1：求刚架内力。 解 （1）基本体系：取 D点水平线位移作为基本 未知量 （2）位移法方程 11 1 1P k F Δ+ = 0 示例 （3）求系数和自由项 ▲作∆1=1时的弯矩图 因为侧移是已知的， 可用力矩分配法计算。 11 k = 0.594

若有两个线位移时，计算步骤如下：3.39924A作M图-2414.CB116NA因为没有侧移，可用（1）基本体系：取两个线位移作为基本未知量。力矩分配法计算。（2）位移法基本方程：1.29Frp=1.16kNk.,A, +k,, + F, =02457_F=-1.95M,(单优kN-m)2A,+k2,+F2p=0A, =-kut47.842.8（3）求系数和自由项，解方程2374（4）作弯矩图<用力矩分配法作出4,=1时的弯矩图，求k、k，18.55.026.7M=M,A,+M,<用力矩分配法作出42=1时的弯矩图，求k12、kz用力矩分配法作出荷载时的弯矩图，求FipF（4）作弯矩图M=M,A+M,A，+MM（单位kN-m8-6近似法1.忽略剪力和轴力引起的变形■计算梁和刚架的位移时，经常略去剪力和轴力的产生的教学内容：变形，计算拱的位移时，也常略去剪切变形。■忽略剪力和轴力引起的变形■超静定梁和刚架的内力计算，由于只考虑弯曲变形而大■在竖向荷载作用下忽略刚架的侧移为简化。通常在位移法、力矩分配法中都采用这个假定。分层法■在水平荷载作用下忽略刚架的结点转角■计算时忽略轴向变形和剪切变形，实际上就是假设杆件反弯点法的抗拉和抗剪刚度无穷大。■在高层建筑中，轴力引起的变形将不能忽略，在截面尺寸大、杆长很小的粗杆中，剪力引起的变形也不容忽视。3.在水平荷载作用下忽略刚架的结点转角2.在竖向荷载作用下忽略刚架的侧移有结点线位移的刚架，虽然在竖向荷载作用下也可以引如果梁的刚度与柱子的线刚度大很多，在水平荷载作用线起侧移，但数值一般比较小。位移是主要位移，转角位移可以忽略。分层计算法假定：反弯点法假定：将横梁简化为刚性梁。（1）忽略侧移的影响，用力矩分配法计算；山H各柱的剪力为F.（2）忽略每层梁的竖向荷载对其他各层的影响，把多层刚架分解成一层一层地单独计算。12i,A=k,AFot=荷载对其它层的影响要经过分配一传递一再分配的过程，因而可以忽略121A=k,A因为假定柱的远端为固定端，而实际各柱都是弹性固定端，Fo2=h2因此将上层各柱的线刚度乘以折减系数0.9，传递系数由1/2变为1/3。柱子的侧移刚度。kik-分层计算的结果在结点上是不平衡的，但误差一般不会很大。如需要，可对结点的不平衡力矩在进行一次分配。9

9 ▲作MP图 因为没有侧移，可用 力矩分配法计算。 1P F = 1.16 kN 1P 1 95 F Δ =1 − = − 11 1.95 k Δ= = （4）作弯矩图 MM M = Δ+ 11 P 若有两个线位移时，计算步骤如下： （1）基本体系：取两个线位移作为基本未知量。 （2）位移法基本方程： 11 1 12 2 1P 21 1 22 2 2P 0 0 kkF kkF Δ + Δ+ = 21 1 22 2 2P Δ + Δ+ = （3）求系数和自由项，解方程 ▲用力矩分配法作出∆1=1时的弯矩图，求 11 21 k k 、 ▲用力矩分配法作出∆2=1时的弯矩图，求 12 22 k k 、 ▲用力矩分配法作出荷载时的弯矩图，求 F1P 2P 、F （4）作弯矩图 MM M M = Δ+ Δ+ 11 22 P 教学内容： 8-6 近似法 „ 忽略剪力和轴力引起的变形 „ 在竖向荷载作用下忽略刚架的侧移 分层法 „ 在水平荷载作用下忽略刚架的结点转角 反弯点法 „ 计算梁和刚架的位移时，经常略去剪力和轴力的产生的 变形，计算拱的位移时，也常略去剪切变形。 „ 超静定梁和刚架的内力计算，由于只考虑弯曲变形而大 为简化 通常在位移法 力矩分配法中都采用这个假定 1. 忽略剪力和轴力引起的变形 。 、力矩分配法中都采用这个假定。 „ 计算时忽略轴向变形和剪切变形，实际上就是假设杆件 的抗拉和抗剪刚度无穷大。 „ 在高层建筑中，轴力引起的变形将不能忽略，在截面尺 寸大、杆长很小的粗杆中，剪力引起的变形也不容忽视。 有结点线位移的刚架，虽然在竖向荷载作用下也可以引 起侧移，但数值一般比较小。 分层计算法假定： （1）忽略侧移的影响，用力矩分配法计算； （2）忽略每层梁的竖向荷载对其他各层的影响，把多层刚 架分解成 地单独计算 2. 在竖向荷载作用下忽略刚架的侧移 架分解成一层一层地单独计算。 荷载对其它层的影响要经过分配—传递—再分配的过程，因 而可以忽略 因为假定柱的远端为固定端，而实际各柱都是弹性固定端， 因此将上层各柱的线刚度乘以折减系数0.9，传递系数由1/2变 为1/3。 分层计算的结果在结点上是不平衡的，但误差一般不会很大 。如需要，可对结点的不平衡力矩在进行一次分配。 如果梁的刚度与柱子的线刚度大很多，在水平荷载作用线 位移是主要位移，转角位移可以忽略。 反弯点法假定：将横梁简化为刚性梁。 各柱的剪力为 3.在水平荷载作用下忽略刚架的结点转角 1 Q1 1 2 1 2 Q2 2 2 2 12 12 i F k h i F k h = Δ= Δ = Δ= Δ k1、k2——柱子的侧移刚度

例1：作刚架弯矩图。顶层由平衡条件，得FothFozhTE28kN GF, = Fo + FQ21TμGD=μIF=ws2×2+3-FOS(2)k.Fo-1=0.286Folk.+k剪力分Foth:17ANDFohL30.428配系数Hen =2×2+3FF02k,+k,底层aL2注：在多层刚架中，通常36m4.5m-荷载F,按剪力分μAD =μFc =3×2+4将底层反弯点设在柱子2/3高解设柱的反弯点在柱子配系数分配给各柱。= 0.3中点高度处。度处。4利用反弯点在柱子中点的0.4（1）求各柱的剪力分配系数AEH=2×2+4性质，可得到柱子两端弯矩。梁端弯矩：将柱端弯矩之和按梁的转动刚度分配（2）计算各柱剪力12Focb=Foir=0.286×8kNSANMz-号*(Mm+Mas)=7.76kNm=2.29kN15FFowForMEr=x(Men+Mga)=9.70kNmFoEn=0.428x8kN2717kN2= 3.42kN2.51.5.643.783.78.&KN.L3.783.13FoaD=Focp=0.3×25kN17.28=7.5kN7.7613.512FoBE=0.4×25kN=10kN17kN13.5（3）计算杆端弯矩（以E点为例）3.785.6.783.3mh,9.7017.28=-3.42kNx-5.46kNmMu=-F.OHEX2=-10kNx3.6mM图（单位KN-m)Men--Fone×=-12kNm3.438-7超静定结构各类解法的比较和合理选用1.基本方程直接解法和渐进解法的比较教学内容：基本方程直接解法：力法和位移法。■基本方程直接解法和渐进解法的比较渐进解法：力矩分配法和无剪力分配法。■在竖向荷载作用下忽略刚架的侧移渐进法的每一步都满足变形协调条件，平衡条分层法件则在最后一步在允许误差内得到满足■在水平荷载作用下忽略刚架的结点转角反弯点法10

10 由平衡条件，得 FP Q1 Q2 = + F F 1 Q1 P 1 2 2 k F F k k k F F = + = 剪力分 配系数 Q2 P 1 2 F F k k = + 荷载FP按剪力分 配系数分配给各柱。 利用反弯点在柱子中点的 性质，可得到柱子两端弯矩。 注：在多层刚架中，通常 将底层反弯点设在柱子2/3高 度处。 例1：作刚架弯矩图。 2 22 3 0.286 3 0.428 22 3 GD IF EH μ μ μ = = × + = = = × + 顶层 解 设柱的反弯点在柱子 中点高度处。 （1）求各柱的剪力分配系数 22 3 × + 2 32 4 0.3 4 0.4 22 4 AD FC EH μ μ μ = = × + = = = × + 底层 （2）计算各柱剪力 Q Q Q 0.286 8kN 2.29 kN 0.428 8 kN 3.42 kN GD IF EH F F F == × = = × = Q Q Q 0.3 25kN 7.5 kN 0.4 25 kN 10 kN AD CF BE F F F = =× = =× = （3）计算杆端弯矩（以E点为例） 2 Q 1 Q 3.3 m 3.42kN 5.46kN m 2 2 3.6 m 10 kN 12 kN m 3 3 EH HE EB BE h M F h M F =− × =− × =− =− × =− × =− - - 12 ( ) 7.76kN m 27 15 ( ) 9.70kN m 27 ED EH EB EF EH EB M MM M MM =× + = =× + = 梁端弯矩：将柱端弯矩之和按梁的转动刚度分配。 7.76 9.70 12 教学内容： 8-7 超静定结构各类解法的比较和合理选用 „ 基本方程直接解法和渐进解法的比较 „ 在竖向荷载作用下忽略刚架的侧移 分层法 „ 在水平荷载作用下忽略刚架的结点转角 反弯点法 基本方程直接解法：力法和位移法。 渐进解法：力矩分配法和无剪力分配法。 渐进法的每 步都满足变形协调条件 平衡条 1. 基本方程直接解法和渐进解法的比较 法的每一步都满足变形协调条件，平衡条 件则在最后一步在允许误差内得到满足