《结构力学》课程教学资源（课件讲稿）第九章 矩阵位移法 9.2 单元刚度矩阵（局部坐标系）

9-2单元刚度矩阵（局部坐标系）教学目标：了解和掌握梁单元、桁架单元、平面刚架单元在局部坐标系的刚度矩阵。教学内容：一般单元单元刚度方程单元刚度矩阵的性质特殊单元

9-2 单元刚度矩阵（局部坐标系） 教学目标： „ 了解和掌握梁单元、桁架单元、平面刚架 单元在局部坐标系的刚度矩阵。 教学内容： „ 一般单元 „ 单元刚度方程 „ 单元刚度矩阵的性质 „ 特殊单元

1.一般单元指杆件除有弯曲变形外，还有轴向和剪切变形的单元杆件两端各有三个位移分量结构的离散化一般单元e①②③④CMAIBIDww多跨梁②①③④EYMACDB??F刚架G000

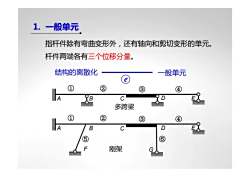
1.  一般单元 ① ② ③ ④ 指杆件除有弯曲变形外，还有轴向和剪切变形的单元。 杆件两端各有三个位移分量。 A B C D E 多跨梁 A B D E ① ② ③ ④ C 刚架 ⑤ ⑥ F G 结构的离散化 e 一般单元

1.一般单元>符号规则凡是符号上面带了一横杠的就表示是基于局部坐标系而言的。局部坐标系EAI21x单元编号?结点编号1e1杆端位移编号uuz2订弯矩、车转角：绕杆端顺时针为正；其它：与坐标轴同向为正MM杆端力编号E后xlx2VFV

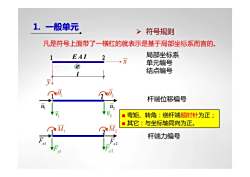
1.  一般单元 ¾ 符号规则 1 2 e E A I l x y 1 2 1 u 1 v θ1 θ2 2 u 2 v 1 2 Fx1 Fy1 M1 M2 Fx2 Fy2 局部坐标系 单元编号 结点编号 杆端位移编号 杆端力编号 ■ 弯矩、转角：绕杆端顺时针为正； ■ 其它：与坐标轴同向为正。 凡是符号上面带了一横杠的就表示是基于局部坐标系而言的

1.一般单元>杆端位移向量>杆端力向量NeGMM16uunx2VFF12124(e(e)(e)(e)历居届丽局国屋区屋屋网O云INA(2)101A(0)((e)F=4(4)iz1v2-A(5)F6A(6)

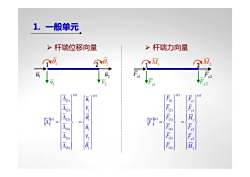
1.  一般单元 1 2 1 u 1 v θ1 θ2 2 u 2 v ¾ 杆端位移向量 ¾ 杆端力向量 1 2 Fx1 Fy1 M1 M2 Fx2 Fy2 { } ( ) 2 2 2 1 1 1 ( ) (6) (5) (4) (3) (2) (1) ( ) e e e v u v u ⎪⎪⎪⎭ ⎪⎪⎪⎬⎫ ⎪⎪⎪⎩ ⎪⎪⎪⎨⎧ = ⎪⎪⎪⎪⎭ ⎪⎪⎪⎪⎬⎫ ⎪⎪⎪⎪⎩ ⎪⎪⎪⎪⎨⎧ Δ Δ Δ Δ Δ Δ Δ = θ θ { } ( ) 2 2 2 1 1 1 ( ) (6) (5) (4) (3) (2) (1) ( ) e y x y x e e M F F M F F F F F F F F F ⎪⎪⎪⎪⎭ ⎪⎪⎪⎪⎬⎫ ⎪⎪⎪⎪⎩ ⎪⎪⎪⎪⎨⎧ = ⎪⎪⎪⎪⎭ ⎪⎪⎪⎪⎬⎫ ⎪⎪⎪⎪⎩ ⎪⎪⎪⎪⎨⎧ =

2.单元刚度方程由单元杆端位移求单元杆端力时所建立的方程xMi务V1M?V20αFxlFx2HPu2Fey2首先在杆端两端加上人为控制的附加约束，使体系发生任意指定的位移然后根据位移推算相应的杆端力

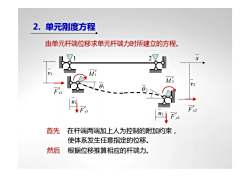
2.  单元刚度方程 由单元杆端位移求单元杆端力时所建立的方程。 首先 在杆端两端加上人为控制的附加约束， 使体系发生任意指定的位移。 然后 根据位移推算相应的杆端力。 1 2 x u1 θ 1 v1 u2 v2 θ 2 e F x1 e F y1 e M 1 e F x2 e F y2 e M 2

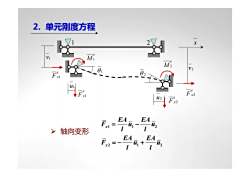
2.单元刚度方程x2MiV1M2V2010Fx13ul1388Fx22Vlu2Fv2EAEAFx111>轴向变形EAEAFu,+x211

2.  单元刚度方程 1 2 x u1 θ 1 v1 u2 v2 θ 2 e F x1 e F y1 e M 1 e F x2 e F y2 e M 2 ¾ 轴向变形 1 12 2 12 x x EA EA F u u l l EA EA F u u l l = − =− +

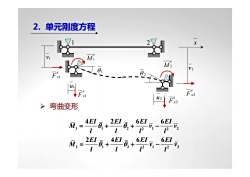
2.单元刚度方程xMiV1M2V2019Fx0ul1388Fx2Fu2Fy2弯曲变形4EI6EI6EI2EI0.0,+MV公+1212112EI6EI4EI6EIAA.M++VVR/

2.  单元刚度方程 1 2 x u1 θ 1 v1 u2 v2 θ 2 e F x1 e F y1 e M 1 e F x2 e F y2 e M 2 ¾ 弯曲变形 1 1 212 2 2 2 1212 2 2 42 66 24 66 EI EI EI EI M v v l lll EI EI EI EI M v v l lll θ θ θ θ =++− =++−

2.单元刚度方程忽略轴向受力状态和弯曲受力状态之间的相互影响，得EAEAFuzNxI112EI6EI6EI12EI云A.y1131?13126EI4EI2EI6EIAM22PP?11EAEAFx2/16EI12EI12EI6EI西FV1y21?1213132EI6EI6EI4EIMAAVVA1217

忽略轴向受力状态和弯曲受力状态之间的相互影响，得 2.  单元刚度方程 1 12 1 12 1 2 22 3 3 1 1 212 2 2 2 12 2 12 1 2 22 3 3 2 1212 2 2 6 6 12 12 42 66 6 6 12 12 24 66 x y x y EA EA F uu l l EI EI EI EI F v v ll l l EI EI EI EI M vv l lll EA EA F uu l l EI EI EI EI F v v ll l l EI EI EI EI M vv l lll θ θ θ θ θ θ θ θ = − =++ − =++− =− + =− − − + =++−

2.单元刚度方程EA4.F0x11Fyl4e)M40Fx2FJ24]M,F=局部坐标系下的一般单元刚度方程

2.  单元刚度方程 1 ( ) 1 1 3 2 32 1 2 2 2 2 32 3 2 2 2 2 00 00 12 6 12 6 0 0 6 4 62 0 0 00 00 12 6 12 6 0 0 6 2 64 0 0 e e x y x y EA EA F l l EI EI EI EI F l l ll EI EI EI EI M l l ll EA EA F l l EI EI EI EI F ll l l EI EI EI EI M l l ll Δ Δ ⎡ ⎤ ⎧ ⎫ − ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ − ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ − ⎪ ⎪ ⎨ ⎬ = ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ − ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ −− − ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎩ ⎭ − ⎢ ⎥ ⎣ ⎦ ( ) ( ) ( ) ( ) ( ) 2 3 4 5 6 e Δ Δ Δ Δ ⎧ ⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎭ { } [ ] { } ( e ) ( e ) ( e ) F = k Δ 局部坐标系下的一般单元刚度方程

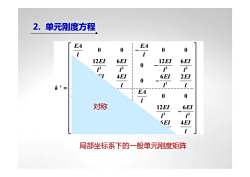
2.单元刚度方程EAEA000016EI12EI6EI12EI01213β3TI4EI6EI2EI01211ke=EA001对称6EI12EI[13[2CEI4EI1局部坐标系下的一般单元刚度矩阵

2.  单元刚度方程 3 2 32 2 2 32 3 2 2 2 00 00 12 6 12 6 0 0 6 4 62 0 0 00 00 12 6 12 6 0 0 6 2 64 0 0 e EA EA l l EI EI EI EI l l ll EI EI EI EI l l ll k EA EA l l EI EI EI EI ll l l EI EI EI EI l l ll ⎡ ⎤ − ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ − = ⎢ ⎥ ⎢ ⎥ −⎢ ⎥ ⎢ ⎥ ⎢ ⎥ −− − ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ ⎣ ⎦ 局部坐标系下的一般单元刚度矩阵 对称