《结构力学》课程教学资源（课件讲稿）第九章 矩阵位移法 9.5 刚架的整体刚度矩阵

回顾一个工具：单元定位向量一个方法：对号入座一个成果：整体刚阵矩阵定位向量K12.2第几号结点位移单元第号位移第儿号结点力单元第号杆端力

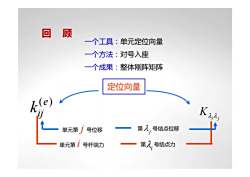
回 顾 一个工具：单元定位向量 一个方法：对号入座 一个成果：整体刚阵矩阵 单元第 i 号杆端力 第 号结点力 λi 单元第 λ j j 号位移 第 号结点位移 (e) ij k i j Kλ λ 定位向量

9-5刚架的整体刚度矩阵教学目标：掌握刚架的整体刚度矩阵的计算教学内容：刚架的特点单元定位向量刚架的整体刚度矩阵结点的处理

9-5 刚架的整体刚度矩阵 教学目标： „ 掌握刚架的整体刚度矩阵的计算。 教学内容： „ 刚架的特点 „ 单元定位向量 „ 刚架的整体刚度矩阵 „ 铰结点的处理

1.刚架的特点关键点：1．用单元集成法形成刚架的整体刚度矩阵[；2.由[K]e通过坐标变换得到[k]e，[K] 由「k]e直接集成;3．换码依据定位向量进行。复杂性：1.刚架中每个结点的位移分量增加到3个，每个单元的杆端位移分量可达6个；2.各杆单元的方向不一致，2种坐标系，坐标变换；3.刚架中含有铰节点时，增加了处理的复杂性

1.  刚架的特点 关键点： 1. 用单元集成法形成刚架的整体刚度矩阵 [K]； 2. 由 [k]e 通过坐标变换得到 [k]e ，[K] 由 [k]e 直接集成； 3. 换码依据定位向量进行。 复杂性： 1. 刚架中每个结点的位移分量增加到 3 个， 每个单元的杆端位移分量可达 6 个； 2. 各杆单元的方向不一致，2 种坐标系，坐标变换； 3. 刚架中含有铰节点时，增加了处理的复杂性

1.刚架的特点结点位移分量的统一编码一一总码、局部码x-y(1)对于已知为零的结点位移分量，其总码均2编为零例9-1的结构04J(△]= [A,△2△Fa1F2F,(F}= [F

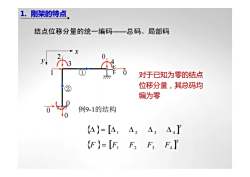
结点位移分量的统一编码——总码、局部码 ① ② x y 0 0 0 1 2 3 0 0 4 { } [ ]T Δ = Δ1 Δ 2 Δ 3 Δ 4 { } [ ]T F = F1 F2 F3 F4 例9-1的结构 对于已知为零的结点 位移分量，其总码均 编为零 1.  刚架的特点

2. 单单元单位向量①②I(1)(1)→I2(2)22→6(3)3y(4)00(4)0>(5)00→(5)→(6)40-(6)→1[1224310000[4][0

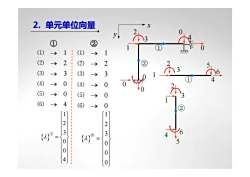
1 2 3 0 0 0 → → → → → → ⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ② 1 2 3 0 0 4 → → → → → → ⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ① ① ② 0 0 0 1 2 3 0 0 4 ① 1 2 3 4 5 6 x y { } 1 2 3 0 0 4 λ ⎧ ⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ = ⎨ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎭ ① { } 1 2 3 0 0 0 λ ⎧ ⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ = ⎨ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎭ ② 2 ② 1 3 4 5 6 2.  单元单位向量

3.刚架的整体刚度矩阵ITT(2)[巴[[k]1]口[K][K]2 巴[k]2d(a]

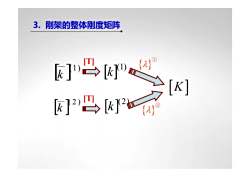
{λ}① [ ](1) k [ ](2) k [T] [T] [K] {λ}② [ ]( 2 ) k [ ](1) k 3.  刚架的整体刚度矩阵

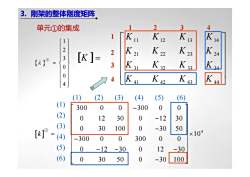
3.刚架的整体刚度矩阵2314单元①的集成FK4K13K/211K24F?K 23K 2222[K ] -=13(a)K 3K.Ka1K 32300KKAK 43K 42N[4](1)(3)(2)(4)(5)(6)(1)0000300-300(2)012030-1230(3)0300100-3050[k]×104= (4)0000300-300(5)0012-30-30-12(6)030010050-30

(1) (2) (3) (4) (5) (6) (1) (2) (3) (4) (5) (6) 单元①的集成 [ ] ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 41 42 43 44 31 32 33 34 21 22 23 24 11 12 13 14 K K K K K K K K K K K K K K K K K 12 3 4 1 2 3 4 [ ] 4 300 0 0 300 0 0 0 12 30 0 12 30 0 30 100 0 30 50 10 300 0 0 300 0 0 0 12 30 0 12 30 0 30 50 0 30 100 k ⎡ ⎤ − ⎢ ⎥ − ⎢ ⎥ ⎢ ⎥ − = × ⎢ ⎥ −⎢ ⎥ ⎢ ⎥ −− − ⎢ ⎥ ⎣ ⎦ − ① { } 1 2 3 0 0 4 λ ⎧ ⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ = ⎨ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎭ ① 3.  刚架的整体刚度矩阵

单元①的集成3.刚架的整体刚度矩阵(1)(2)(3)(4)(5)(6)(1)0000300-300(2)001230-1230(3)003050100-3010[k]x104二(4)0000300-300(5)00-12-3012-30(6)003050100-300003000123030[K]×1040305010005030100

[ ] 4 300 0 0 0 0 12 30 30 10 0 30 100 50 0 30 50 100 K ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ × ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ① (1) (2) (3) (4) (5) (6) (1) (2) (3) (4) (5) (6) [ ] 4 300 0 0 300 0 0 0 12 30 0 12 30 0 30 100 0 30 50 10 300 0 0 300 0 0 0 12 30 0 12 30 0 30 50 0 30 100 k ⎡ ⎤ − ⎢ ⎥ − ⎢ ⎥ ⎢ ⎥ − = × ⎢ ⎥ −⎢ ⎥ ⎢ ⎥ −− − ⎢ ⎥ ⎣ ⎦ − ① 3.  刚架的整体刚度矩阵 单元①的集成

3.刚架的整体刚度矩阵1234单元②的集成Ki41KK12K13[1]K 2K 23K 24K21[K ] =2K31K 34K 33K 32322）K 43K 42K 41K 44J2400(1)(3)(5)(6)(2)(4)(1)012-300-12[0]-30(2)0000300-300(3)01000-303050[kj2]×104(4)03001230-120(5)000300-30005030030(6)100]

{ } 1 2 3 0 0 0 λ ⎧ ⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ = ⎨ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎭ ② [ ] ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 41 42 43 44 31 32 33 34 21 22 23 24 11 12 13 14 K K K K K K K K K K K K K K K K K 12 3 4 1 2 3 4 [ ](2) 4 10 30 0 50 30 0 100 0 300 0 0 300 0 12 0 30 12 0 30 30 0 100 30 0 50 0 300 0 0 300 0 12 0 30 12 0 30 × ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − − k = (1) (2) (3) (4) (5) (6) (1) (2) (3) (4) (5) (6) 单元②的集成 3.  刚架的整体刚度矩阵

3.刚架的整体刚度矩阵单元②的集成(2)(3)(4)(1)(5)(6)(1)012-300-12-30(2)0000300-300(3)00501003030[kj]2]×104(4)00301230-12(5)0000-30030000305030(6)1000-3012[K] =×104003000L-30100

[ ](2) 4 10 30 0 50 30 0 100 0 300 0 0 300 0 12 0 30 12 0 30 30 0 100 30 0 50 0 300 0 0 300 0 12 0 30 12 0 30 × ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − − k = (1) (2) (3) (4) (5) (6) (1) (2) (3) (4) (5) (6) [ ] 4 10 30 0 100 0 300 0 12 0 30 × ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − = ② K 3.  刚架的整体刚度矩阵 单元②的集成