《结构力学》课程教学资源（课件讲稿）第九章 矩阵位移法 9.6 等效结点荷载

9-6等效结点荷载教学目标：掌握等效结点荷载的计算。理解等效结点荷载的概念。教学内容：结点荷载与非结点荷载单元集成法求等效结点荷载

9-6 等效结点荷载 教学目标： „ 掌握等效结点荷载的计算。 „ 理解等效结点荷载的概念。 教学内容： „ 结点荷载与非结点荷载 „ 单元集成法求等效结点荷载

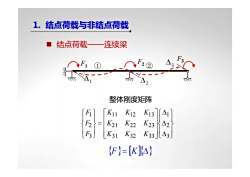
1.结点荷载与非结点荷载结点荷载-连续梁LTAT△T整体刚度矩阵FiK11K12[41K13F2 (=K21K22K23BA2[F3][K31K32K33/[43(F}=[KA)

„ 结点荷载——连续梁 F1 F2 F3 Δ1 Δ2 ① ② Δ3 ⎪⎭ ⎪⎬⎫ ⎪⎩⎪⎨⎧ΔΔΔ ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ = ⎪⎭⎪⎬⎫ ⎪⎩⎪⎨⎧ 321 31 32 33 21 22 23 11 12 13 321 K K K K K K K K K FFF {F}= [K]{Δ} 整体刚度矩阵 1.  结点荷载与非结点荷载

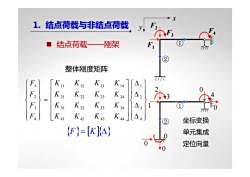
X1.结点荷载与非结点荷载FVF3①F结点荷载一刚架-P2整体刚度矩阵T7T7K/2Kr3KFK 14△10K 21F2K 22K 24K 23423K 31FsK 32K33K 34△3①1TPTTF4)[K 41K 42K 43K 4444坐标变换2(F}=[KA)单元集成定位向量

① ② 0 0 0 1 2 3 0 0 4 x y ① ② F1 F2 F3 F4 坐标变换 单元集成 定位向量 { } F = [K ] {Δ } ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ Δ Δ Δ Δ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ 4 3 2 1 41 42 43 44 31 32 33 34 21 22 23 24 11 12 13 14 4 3 2 1 K K K K K K K K K K K K K K K K F F F F 整体刚度矩阵 „ 结点荷载——刚架 1.  结点荷载与非结点荷载

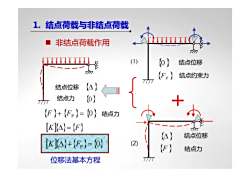
1.结点荷载与非结点荷载非结点荷载作用TP(1)(0)结点位移TPIT(Fp)结点约束力TT(4)结点位移(0)结点力+7777(F)+ (Fp)= (0)结点力[K}= {F}(4)结点位移[K JA)+ (F]= (0)(2)(F)结点力T7位移法基本方程

{Δ} {0} 结点位移 结点力 (1) (2) {F } 结点力 {Δ} 结点位移 {FP } 结点约束力 {0} 结点位移 {F }{ } + FP = {0} 结点力 1.  结点荷载与非结点荷载 [K]{} {} Δ = F [K]{} { } Δ + FP = {0} 位移法基本方程 „ 非结点荷载作用

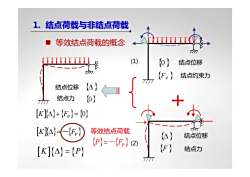
1.结点荷载与非结点荷载等效结点荷载的概念TPT(1)(0)结点位移TPIT(Fp)结点约束力TT(4)结点位移(0)结点力+7777[K]A]+ (Fp}= (0](-(F)[KA}-等效结点荷载(4)结点位移(P)=-(Fp) (2)(F)结点力[K](A] = (P)TTT

{Δ} {0} 结点位移 结点力 (1) (2) {F } 结点力 {Δ} 结点位移 {FP } 结点约束力 {0} 结点位移 1.  结点荷载与非结点荷载 „ 等效结点荷载的概念 [K]{Δ} {} =－ FP [ ] K {Δ}{ } + FP = {0} [K P ]{Δ =} { } 等效结点荷载 {P}=－{FP}

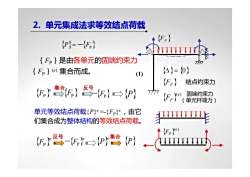
2.单元集成法求等效结点荷载H(P)=-{Fp)【Fp】是由各单元的固端约束力TP1T(}= (0)【Fp）(e)集合而成。(1)(Fp)结点约束力集合(反号(F)(Fp)e-{F)>(P)1固端约束力(F,e)（单元杆端力）单元等效结点荷载(P)e=-{Fp)e，由它们集合成为整体结构的等效结点荷载Fp(F)-(F(P) (P)

{FP } { }(e) FP {Δ}= {0} {FP } 结点约束力 固端约束力 （单元杆端力） (1) { }(e) FP { }P =－{FP } ｛FP｝是由各单元的固端约束力 ｛FP｝(e) 集合而成。 单元等效结点荷载{P}e =-{FP}e，由它 们集合成为整体结构的等效结点荷载。 { }e FP { } FP －{FP} {P} 集合 反号 { }e FP { }e － FP { }e P {P} 反号 集合 2.  单元集成法求等效结点荷载

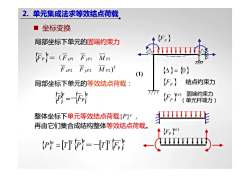
2.单元集成法求等效结点荷载坐标变换Fp局部坐标下单元的固端约束力(Fp=(Fxpl Fypl MpTP1TFxp2 Fyp2 Mp2)(}= (0)(1)(Fp)结点约束力局部坐标下单元的等效结点荷载：777固端约束力(F,10)(=（单元杆端力）整体坐标下单元等效结点荷载P!e一再由它们集合成结构整体等效结点荷载Fp(P=[=-

{ } T xP yP P xP yP P e F F M F F F M 2 2 2 ) P ＝（ 1 1 1 „ 坐标变换 { } { } e e P =－FP 局部坐标下单元的等效结点荷载： 局部坐标下单元的固端约束力 整体坐标下单元等效结点荷载{P}e ， 再由它们集合成结构整体等效结点荷载。 { } [ ] { } [ ] { } e e e P T P T FP T T = ＝－ {FP } { }(e) FP {Δ}= {0} {FP } 结点约束力 固端约束力 （单元杆端力） (1) { }(e) FP 2.  单元集成法求等效结点荷载

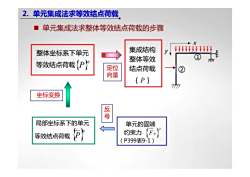
2.单元集成法求等效结点荷载单元集成法求整体等效结点荷载的步骤集成结构整体坐标系下单元(1)整体等效(P)等效结点荷载定位结点荷载向量(P)TTTT坐标变换反号←局部坐标系下的单元单元的固端2(p)约束力{FP等效结点荷载（P399表9-1）

„ 单元集成法求整体等效结点荷载的步骤 单元的固端 约束力 （P399表9-1）{ P }e F { }e P 局部坐标系下的单元 等效结点荷载 集成结构 整体等效 结点荷载 ｛P｝ 定位 向量 反 号 坐标变换 x y ① ② 整体坐标系下单元 等效结点荷载{ }e P 2.  单元集成法求等效结点荷载

2.单元集成法求等效结点荷载4.8kN/m■示例3①1例9-3求图示刚架等效结点荷载。T②8kN解:（1）局部坐标系下固端约束力(F,5mTTT（查表9-1）(F)=Fxpl Fypl Mp Fxp2 Fyp2 Mp2]=[0 -12 -10 0 -12 10](F,-[Fxpl Fypl Mp Fxp2 Fyp2 Mp]=[0 4 5 0 4 -

例9-3求图示刚架等效结点荷载。 ① ② 4.8kN/m 8kN 1 3 2 4 解： （1）局部坐标系下固端约束力 { } e FP （查表9-1） { } [ ] [ ] T T P xP yP P xP yP FP F F M F F M 0 12 10 0 12 10 2 2 2 1 1 1 1 = − − − = { } [ ] [ ] T T P xP yP P xP yP FP F F M F F M 0 4 5 0 4 5 2 2 2 1 1 1 2 = − = 5m „ 示例 2.  单元集成法求等效结点荷载

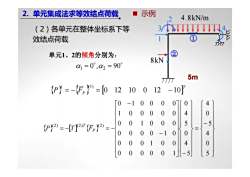
■示例2.单元集成法求等效结点荷载4.8kN/m3（2）各单元在整体坐标系下等①1效结点荷载TP②单元1、2的倾角分别为：8kNα1 = 0°,α2 = 90°5mTTTT-10]0(P)}=-{F, =[0121012[o00007-104004000010000051-5(P)2) = -[7]2)T (Fp](2) =000000-1400001040Lo0000[5]1J(-5)

（2）各单元在整体坐标系下等 效结点荷载 单元 1 、 2 的倾角分别为： D D α1 = 0 ,α2 = 90 { } { } [ ] T P FP 0 12 10 0 12 10 1 (1) = − = − { } [ ] { } ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ − = ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ − ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − = − = − 5 0 4 5 0 4 5 4 0 5 4 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 (2) (2) (2) P T P T F 2.  单元集成法求等效结点荷载 „ 示例 ① ② 4.8kN/m 8kN 1 3 2 4 5m