《结构力学》课程教学资源（课件讲稿）第七章 位移法

第7章位移法教学目标第7章位移法■了解位移法基本体系与典型方程的物理概念；■掌握位移法基本未知量的判断；DisplacementMethod熟悉等截面杆件的转角位移方程；■熟练掌握用位移法计算各种作用下的结构内力。第7章位移法14kN6教学内容7-1 位移法的基本概念2m2m7-2等截面杆件的刚度方程力法求解：三个多余未知力解三元一次方程7-3无侧移刚架的计算7-4有侧移刚架的计算未知位移角度：一个未知位移解一元一次方程7-5位移法的基本体系007-6对称结构的计算（思考）7-7支座移动和温度改变时的计算27-1位移法的基本概念1. 引例EAEA教学要求：2图示变截面梁。求AB、BC段的内力。■理解位移法的基本原理■建立刚度方程的基本概念整体分析位移■掌握位移法解题的基本过程离散几B主要内容：位4日Nar杆端力与位杆件分析移■引例BCN移的关系法集合 Λ 个■位移法基本原理列平衡方■位移法解题步骤整体分析NBANBC程求位移BFCA

1 Displacement Method 第 7 章 位移法 Displacement Method 第 7 章 位移法 „ 了解位移法基本体系与典型方程的物理概念； „ 掌握位移法基本未知量的判断； 教学目标 „ 熟悉等截面杆件的转角位移方程； „ 熟练掌握用位移法计算各种作用下的结构内力。 第 7 章 位移法 7-1 位移法的基本概念 7-2 等截面杆件的刚度方程 7 3 无侧移刚架的计算 教学内容 - 无侧移刚架的计算 7-4 有侧移刚架的计算 7-5 位移法的基本体系 7-6 对称结构的计算 7-7 支座移动和温度改变时的计算 14kN A B C 2m 4m 力法求解： 三个多余未知力 解三元 次方程 θ 2m 力法求解： 三个多余未知力 解三元一次方程 未知位移角度： 一个未知位移 解一元一次方程 思考 教学要求： 7-1 位移法的基本概念 „ 理解位移法的基本原理 „ 建立刚度方程的基本概念 „ 掌握位移法解题的基本过程 主要内容： „ 引例 „ 位移法基本原理 „ 位移法解题步骤 „ 掌握位移法解题的基本过程 a a EA1 EA2 AB C F 图示变截面梁。 ¾ 整体分析 位移 Δ NBA Δ 求AB、BC段的内力。 1. 引例 ¾ 杆件分析 杆端力与位 移的关系 A B NBA C NBC B ¾ 整体分析 列平衡方 程求位移 A B C F NBA NBC 位 移 法 离散 集合

3.位移法解题步骤2.位移法基本原理M图示两跨梁，求杆114kNBAAX端弯矩。EI为常数，忽1A略杆件的轴向变形。47O2m>整体分析2m0g.4m基本未知量MAs离散几A（1）结构的独立结点位移》杆件分析移ne法CoO假定顺时针1↑M Ma Mnc>整体分析7i0g-Mg=0BBB基本方程14kN7114kNB0g82m4m2m2m4m（2）结构拆成杆件，做杆件分析i0, =1杆端弯矩一荷载和变形（4）回代，求杆端弯矩Mg=7+4i0,MAB=-7+2i0M gc = 3i0^Mca =0Ma =7+4i0,=3MB=-7+2i0, =-9（3）平衡方程，求解Mrc = 3i0, = 3Mcn=0M,-0=Mu+M-0→7+710,=0=10,=-17-2等截面杆件的刚度方程4.小结（1）等截面梁的形常数杆端位移引起的杆端内力称为形常数》位移法的基本原理i=-EII-一线刚度“化整为零、集零为整”单跨超静定梁简图MABMBA（1）结构的独立结点位移2i4iHB（2）结构拆成杆件，做杆件分析一荷载、变形（3）平衡方程，求解3i0（4）回代，求杆端弯矩--i52

2 图示两跨梁，求杆 端弯矩。EI为常数，忽 略杆件的轴向变形。 ¾ 整体分析 a a AB C MB θB θB θB 2. 位移法基本原理 ¾ 杆件分析 ¾ 整体分析 位 移 法 A B MBA MAB B C θB MBC A B C MBA MBC MB B B 离散 7 0 B B i M θ − = 基本未知量 基本方程 14kN A B C 2m 2m 4m 3. 位移法解题步骤 （1）结构的独立结点位移 θB 假定顺时针 14kN A B C 2m 2m 4m θB （2）结构拆成杆件，做杆件分析 杆端弯矩—荷载和变形 7 4 MBA A = + iθ 7 2 M AB A =− + iθ 3 MBC A = iθ 0 MCB = （3）平衡方程，求解 0 0 ∑ M MM B BA BC =⇒ + = 77 0 1 A A ⇒ + = ⇒ =− i i θ θ 14kN A B C 2m 2m 4m θB 1 A iθ = − （4）回代，求杆端弯矩 74 3 M i BA A = + = θ 72 9 M i AB A =− + =− θ 3 3 M i BC A = θ = − 0 MCB = ¾ 位移法的基本原理 “化整为零、集零为整” 4. 小 结 （1）结构的独立结点位移 （2）结构拆成杆件，做杆件分析—荷载、变形 （3）平衡方程，求解 （4）回代，求杆端弯矩 杆端位移引起的杆端内力称为形常数. （1）等截面梁的形常数 i=EI/l —— 线刚度 7-2 等截面杆件的刚度方程 单跨超静定梁简图 MAB MBA 4i 2i θ=1 A B A θ=1 B 3i 0 A θ=1 B i -i

（2）等载面梁的载常数荷载引起的杆端内力称为载常数。单跨超静定梁简图MABMBAY表7-1等数面杆件的固端宠矩和剪力4=1-6ill-6illHB编+百阁国嘴奢距（以娱时针转向为正）调瑞剪力mMu=-f2Fuu号4=1-3ill0PBMu-Fau=-号Mfo--Fou-岗4=100Ma---3EMa--FonfaFAs=qlMa--1FOR=DMa--%For-fo到FalFan-IF,Fow=FpMa=-3F.lBb-Fua=Fp16Ma=Mu=-F!Frau--ir,Fan=027-3无侧移刚架的计算》连续梁P=20kNq=2kN/m无侧移刚架LCEPRLOEI刚架各节点（不含支座）只有角位移而没有线位移。k 3m ↓ 3m ±6m连续梁属于这类问题。（1）基本末知量6g_Pl_20×6=15kN-m（2）固端弯矩meXXma=-15kN.mql2=-9kN.mmgc3

3 单跨超静定梁简图 MAB MBA A B Δ=1 -6i/l -6i/l -3i/l 0 0 0 A B Δ=1 A B Δ=1 荷载引起的杆端内力称为载常数。 （2）等截面梁的载常数 无侧移刚架 刚架各节点（不含支座）只有角位移而没有线位移。 7-3 无侧移刚架的计算 连续梁属于这类问题。 A B C 3m 3m 6m EI EI P=20kN q=2kN/m θB ¾ 连续梁 （1）基本未知量θB （2）固端弯矩 kN m Pl mBA = ⋅ × = = 15 8 20 6 8 mAB = −15kN ⋅m kN m ql mBC = − = −9 ⋅ 8 2

M=2i0.-15（3）列杆端转角位移方程Ma=4i0g+15MBc=3i0,-96MaPoMec(5)各杆端弯矩及弯矩图0, =-M716）OBEIMaAM.R=2115=16.72kV·m11（Pl=×20×6=30设i=E4M=2i0g-154Mac=3i0g-9Met=4(-6)6+15=11.57kN.m7iIq=↓×2x6=9MBu=4i0g+156Mec=3i-9=-11.57kN-m8Ti（4)位移法基本方程（平衡条件）6.72ZM,=0Ma, +Mac =01.5MaS4i0g+15+30g-9=0之LM图(KN-m):0,--07iM=3i0g+40》刚架（1）基本未知量gec（2）杆端弯矩Mc=4i0g+2i0c-41.7MBe=3i0g20kN/m20kN/mi=El,/lDDMc=4i0c+2i0g+41.7更型AC 410 -Ma=3i0g +40C 4l =--6- 4l0B 5l0-- 41B510Mc = 3i0c310导3%导Moc=4i0g+2i0-41.7Mcr =2i0c31.31。Mcs = 4i0.+2i0,+41.7（4）求未知量EE0g =1.15Mecn =3i0cF（3）位移法方程0g=4.89MBe=3i0gMen=1.5i0g1ZM=0=M+MBc+ME=0（5）求杆端弯矩Mcr=2i0cMrc=i0cZMc=0= McB+Mcp+Mcr=0（6）绘弯矩图57-4有侧移刚架的计算1.位移法的基本未知量结点的位移（线位移、铰位移）有侧移刚架（1）角位移的数目（未知量）=刚结点数刚架除有结点转角外，还有结点线位移。（2）线位移未知量数目基本思路不考虑轴向变形与无侧移刚架基本相同，但增加：弯曲变形小，受弯矩长度不变。>未知量有结点位移；一般方法：取铰接体系：>杆件计算需考虑结点位移；结点线位移数=自由度数>基本方程增加与结点位移对应的平衡方程。=使铰结体系为几何不变体系所必加的最少铰链杆数4

4 q θB EI P EI θB MBA MAB MBC (3) 列杆端转角位移方程 M AB = 2iθ B −15 = 3 −9 BC B M iθ 6 EI 设i = = 4 +15 BA B M iθ (4) 位移法基本方程（平衡条件） i i i M M M B B B B BA BC 7 6 4 15 3 9 0 0 0 ∴ = − + + − = ∑ = + = θ θ θ MBA MBC = 2 −15 AB B M iθ M BA = 4iθ B +15 = 3 − 9 BC B M iθ kN m i M i AB ⎟ − = − ⋅ ⎠ ⎞ ⎜ ⎝ ⎛ = − 15 16.72 7 6 2 kN m i M i BA ⎟ + = ⋅ ⎠ ⎞ ⎜ ⎝ ⎛ = − 15 11.57 7 6 4 (5) 各杆端弯矩及弯矩图 i B 7 6 θ = − 20 6 30 4 1 4 1 Pl = × × = 16.72 11.57 ⎝ 7i ⎠ kN m i M i BC ⎟ − = − ⋅ ⎠ ⎞ ⎜ ⎝ ⎛ = − 9 11.57 7 6 3 M图 ( ) kN ⋅m 2 6 9 8 1 8 1 2 2 ql = × × = 4I 4 0 I0 5I0 3I0 3I0 A B C D m 4m （1）基本未知量θB、θC （2）杆端弯矩 3 40 M i BA B = + θ 4 2 41.7 Mii BC B C =+− θ θ 0 20kN/m i EI l = / ¾ 刚架 0 E F 4m 5m 4m 6m 4 2 41.7 Mii CB C B =++ θ θ 3 MCD C = iθ 3 1.5 MBE B EB B = = iM i θ θ 2 MCF C FC C = = i Mi θ θ 4I 4 0 I0 5I0 3I0 3I0 A B C D 4m 4 2 41.7 Mii BC B C = θ + − θ 4 2 41.7 Mii CB C B =++ θ θ 3 MCD C = iθ 3 MBE B = iθ 2 MCF C = iθ 3 40 M i BA B = θ + 20kN/m 0 E F （3）位移法方程 0 0 0 0 B BA BC BE C CB CD CF M MMM M MMM = ⇒++= = ⇒++= ∑ ∑ （4）求未知量 1.15 4.89 B C θ θ = = − （5）求杆端弯矩 （6）绘弯矩图 有侧移刚架 刚架除有结点转角外，还有结点线位移。 基本思路 7-4 有侧移刚架的计算 与无侧移刚架基本相同，但增加： ¾ 未知量有结点位移； ¾ 杆件计算需考虑结点位移； ¾ 基本方程增加与结点位移对应的平衡方程。 结点的位移（线位移、铰位移） （1）角位移的数目（未知量）= 刚结点数 1. 位移法的基本未知量 （2）线位移未知量数目 ¾ 不考虑轴向变形 ¾ 弯曲变形小，受弯矩长度不变。 一般方法： 取铰接体系： 结点线位移数 = 自由度数 = 使铰结体系为几何不变体系所必加的最少铰链杆数

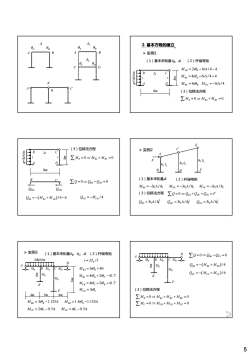
12.基本方程的建立0>实例14s（1）基本未知量6g4（2）杆端弯矩67M=2i0g-6i△/4-4EB2iCMu=4i0g-6iA/4+4Z日SAMpc = 6i0 Mpc =3i△/4P8m（3）位移法方程ZM.=0=M+Mc=0（3）位移法方程>实例2B2i闻ZMg=0=M+MBc=0hylDhz /2h,1,8mBD人（1）基本未知量4B（2）杆端弯矩ZQ=0=Q+Qcp=0Mμ=3i,A/hMpc=-3iz4/hM=-3iA/hQBAQcD（3）位移法方程ZQ=0=Qu+Q0c+Qm=FQcp = -Mcp /4Q=-(Ma, +M)/46Qm=3i,A/h2Q=3,A/hOpc=3i,A/ h>实例3（1）基本未知量g04（2）杆端弯矩D型ZQ=0=Q+Qc=020kN/mB5l410C4.Ai=El,/lDQBe =-(MBe +Mee)/4早310Ma4 = 3i0 +40410B5l041031Qcp = -(Mce + Mpc)/631,Mec=4i0g+2i0.-41.7E1Mce=4i0。+2i0,+41.7F（3）位移法方程Mcp=3i04mZMg=0=Ma+MBc+ME=0M=3i0.-1.125△MeB=1.5i0-1.125△Mc=0=McB+Mcp+Mcr=0Mrc =i0-0.52Mcr=2i0c-0.55

5 A B θA θB Δ θA θB Δ1 A B C D θC θD Δ2 A B C Δ ¾ 实例1 /m B 2i C （1）基本未知量θB、Δ （2）杆端弯矩 2 6 /4 4 Mii AB B = −Δ − θ 2. 基本方程的建立 q=3kN/ 8m 4m A D 2i i i 4 6 /4 4 MBA B = −Δ + i i θ 6 MBC B = iθ 3 /4 M i DC = − Δ （3）位移法方程 0 0 ∑ M MM B BA BC =⇒ + = B C q=3kN/m 8m 4m A D 2i i i （3）位移法方程 0 0 ∑ M MM B BA BC =⇒ + = B C QBA QCD 0 0 ∑Q QQ =⇒ + = BA CD ( ) /4 6 Q MM BA BA AB =− + − / 4 Q M CD CD = − ¾ 实例2 B D F A C E h1 I1 h2 I2 h3 I F 3 （1）基本未知量Δ （2）杆端弯矩 1 1 3 / MBA = − Δi h （3）位移法方程 2 2 3 / MDC =− Δi h 3 3 3 / MFE = − Δi h 0 ∑Q QQ Q F = ⇒++= BA DC FE 2 1 1 3 / Q ih BA = Δ 2 2 2 3 / Q ih DC = Δ 2 3 3 3 / Q ih FE = Δ ¾ 实例3 4I 4 0 I0 5I0 3I0 3I0 A B C D m 4m （1）基本未知量θB、θC、Δ （2）杆端弯矩 3 40 M i BA B = + θ 4 2 41.7 Mii BC B C =+− θ θ 0 20kN/m i EI l = / 0 E F 4m 5m 4m 6m 4 2 41.7 Mii CB C B =++ θ θ 3 MCD C = iθ 3 1.125 1.5 1.125 Mi M i BE B EB B =− Δ = − Δ θ θ 2 0.5 0.5 M i Mi CF C FC C = −Δ = −Δ θ θ 4I 4 0 I0 5I0 3I0 3I0 A B C D E 4m 0 0 ∑Q QQ =⇒ + = BE CF ( ) / 4 Q MM BE BE EB =− + ( ) / 6 Q MM CF CF FC =− + F （3）位移法方程 0 0 0 0 B BA BC BE C CB CD CF M MMM M MMM = ⇒++= = ⇒++= ∑ ∑

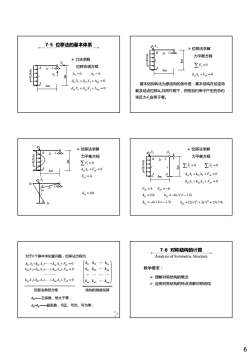
7-5位移法的基本体系14>位移法求解A力平衡方程ttT>力法求解ZF=0位移协调方程A1+1A,042-0k,A,+Fp=08.,X,+82X, +4p =0基本结构转化为原结构的条件是：基本结构在给定荷4m8,X,+82,X, +A2p =0载及结点位移△，共同作用下，在附加约束中产生的总约束反力F应等于零。>位移法求解》位移法求解力平衡方程力平衡方程ZR=0ZF=0ZF=0kiA,+Fip=0k,A, +k2A, +Fi, = 0Fp=414k,A, +kz,+Fp =0Fip=4 Fp=-661ki, =10ik, =10ik2, = -6i //= -1.5ikiz=-6i/4=1.5ik,=12i/P+3i/P=15i/16427-6对称结构的计算对于n个基本未知量问题，位移法方程为Analysisof Symmetric Structure(kkz..kak.4,+k24,+-+k,4,+F, =0教学要求：kn...kznk2,4,+k2A,+..+k.A,+F2p=0k.1》理解对称结构的概念kaA,+kA,+..+kmA,+F.p=0ka.k....k.应用对称结构的特点求解对称结构位移法典型方程结构的刚度矩阵k主系数，恒大于零；k=k——副系数，可正、可负、可为零；26

6 B C N/m 2i ¾ 力法求解 X X2 位移协调方程 1 Δ = 0 2 Δ = 0 7-5 位移法的基本体系 q=3kN 4m 4m A i X1 1 Δ 0 11 1 12 2 1 0 X X P δ + +Δ = δ 2 Δ 0 21 1 22 2 2 0 X X P δ + +Δ = δ B C q=3kN/m 4m 4m A 2i i ¾ 位移法求解 力平衡方程 1 ∑F = 0 k F Δ+ = 0 Δ1 11 1 1 0 P k F Δ+ = 基本结构转化为原结构的条件是：基本结构在给定荷 载及结点位移Δ1共同作用下，在附加约束中产生的总约 束反力F1应等于零。 B C q=3kN/m 4m 4m A 2i i ¾ 位移法求解 力平衡方程 1 ∑F = 0 11 1 1 0 P k F Δ+ = 1 4 F P = B C A 2i i Δ1 1 4 F P 4i 2i 6i 11 k i =10 B C q=3kN/m 4m 4m A 2i i Δ1 D Δ2 i ¾ 位移法求解 力平衡方程 1 ∑F = 0 11 1 12 2 1 0 P kk F Δ+ Δ+ = 2 ∑F = 0 4m 1 4 F P = 2 6 F P = − 21 1 22 2 2 0 P kk F Δ+ Δ+ = 11 k i =10 21 k il i = − =− 6 / 1.5 12 ki i = − =− 6 / 4 1.5 2 2 22 k il il i = += 12 / 3 / 15 /16 对于n个基本未知量问题，位移法方程为 11 1 12 2 1 1P 21 1 22 2 2 2 P 0 0 0 n n n n kk k F kk k F kk k F ΔΔ Δ ΔΔ Δ ΔΔ Δ + ++ + = + ++ + = + ++ + = " " """" 11 12 1 21 22 2 n n kk k kk k kk k ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ " " """" 11 2 2 P 0 n n nn n n kk k F ΔΔ Δ + ++ + = " 位移法典型方程 n n nn 1 2 kk k ⎜ ⎟ ⎝ ⎠ " 结构的刚度矩阵 kii——主系数，恒大于零； kij=kji——副系数，可正、可负、可为零； 教学要求： ¾ 理解对称结构的概念 Analysis of Symmetric Structure 7-6 对称结构的计算 ¾ 应用对称结构的特点求解对称结构

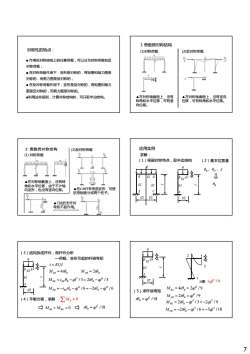
1奇数跨对称结构对称性的特点：(1)对称荷载(2)反对称荷载家家家发家育馆■作用在对称结构上的任意荷载，可以分为对称荷载和反对称荷载；■在对称荷载作用下，变形是对称的，弯矩图和轴力图是ZC对称的，而剪力图是反对称的；■在反对称荷载作用下，变形是反对称的，弯矩图和轴力图是反对称的，而剪力图是对称的。>在对称轴截面上，没有人在对称轴截面上，没有竖向利用这些规则，计算对称结构时，可只取半边结构。转角和水平位移，可有竖位移，可有转角和水平位移。向位移。应用实例2偶数跨对称结构(2)反对称荷载(1)对称荷载求解：（1）根据对称特点，取半边结构（2）基本位置量0g04++★1EIL在对称轴截面上，没有转OB角和水平位移，由于不计轴<柱CD只有弯曲变形，可按向变形，也没有竖向位移。抗弯刚度分成两个柱子F3OL12AC处的支杆对弯矩不起作用。（3）结构拆成杆件，做杆件分析一荷载、变形引起的杆端弯矩i=EI/lBEIEIAMB=4i0BMAB=2i0FMBe=igeOg-q2/3=2i0g-ql?/31/2M图xql/9MB=4i0,=2l2/9M=-ge0g-ql2/6=-2i0,-ql/612（5）求杆端弯矩MAB=2i0g=qI/9（4）平衡方程，求解ZM=0i0g=qt?/18MBe=2i0g-ql?/3=-2q?/9MB+ME=0i0g=qI?/18M=-2i0g-ql/6=-5ql/18

7 ■ 作用在对称结构上的任意荷载，可以分为对称荷载和反 对称荷载； ■ 在对称荷载作用下，变形是对称的，弯矩图和轴力图是 对称性的特点： 对称的，而剪力图是反对称的； ■ 在反对称荷载作用下，变形是反对称的，弯矩图和轴力 图是反对称的，而剪力图是对称的。 ■利用这些规则，计算对称结构时，可只取半边结构。 (1)对称荷载 (2)反对称荷载 1 奇数跨对称结构 ▲在对称轴截面上，没有 转角和水平位移，可有竖 向位移。 ▲在对称轴截面上，没有竖向 位移，可有转角和水平位移。 (1) 对称荷载 2 偶数跨对称结构 (2)反对称荷载 ▲在对称轴截面上，没有转 角和水平位移，由于不计轴 向变形，也没有竖向位移。 ▲柱CD只有弯曲变形，可按 抗弯刚度分成两个柱子。 ▲C处的支杆对 弯矩不起作用。 求解： （1）根据对称特点，取半边结构 B EI D q q B E （2）基本位置量 θB、 θD 、Δ 应用实例 l/2 l EI EI EI A B D C l/2 l l/2 EI A B EI E θB （3）结构拆成杆件，做杆件分析 q —荷载、变形引起的杆端弯矩 l EI B EI E 4 MBA B = iθ i EI l = 2 M AB B = iθ 2 2 M i ql i ql = = θ θ /3 2 /3 l/2 A /3 2 /3 M i ql i ql BE BE B B = θ θ − = − 2 2 /6 2 /6 M i ql i ql EB BE B B =− − =− − θ θ （4）平衡方程，求解 0 ∑ MB = 0 M M BA BE + = 2 /18 B i ql θ = q l l/2 EI A B EI E 2 l / 2 1 5 l/2 2 4 2 /9 M i ql BA B = = θ 2 2 /9 M i ql AB B = = θ 2 2 2 /3 2 /9 M i ql ql BE B = − =− θ 2 2 2 / 6 5 /18 M i ql ql EB B =− − =− θ （5）求杆端弯矩 2 /18 B i ql θ = M图 2 ×ql / 9

作图示结构内力图。吊杆的E4等于横梁E/的1/20m2。（4）求杆端力解（1）半边结构,EIRA46EIAT杆ABMA=2iAn0-6iB02034（2）基本末知量4=10kN/m1L取结点B的转角6和竖向6EIA-EL.20.mm20.m位移<为基本未知量。M=4i0-6iN48120220RKK12EIM+MAR6EIFOA=--0+42022031HbEL-333基本体系半边结构Mac=ianO+ME.杆BC10（3)固端力ElM=-9F__10×10Foec=ql=10×10=100kN=333kN·m0167Mcn=-ias+Mcn3310Focg = 0_10×102gpFonc=Fae=100M=-167kN·m66EI杆BDID0.300.0154 333EA(320(35080794004FNBD=EI0=1(525(54=EI100EI3EI3EI0.0150+0.002224=4=/EIJNB'I5×20×252500（5）最终杆端力（5）列位移法方程26(5080)2(7940) -682N-mM=考虑B点平衡20ZM,=0,Mau +MBc =064(5080)FNBD(79400)=-174kN-mMuMBA202MBC204ZF =0,2Fna +Foa -Fone = 0126MBI(5080)+(79400)= 42.8kNFoec20220FQBAFQBC17-7支座移动和温度改变时的计算Mec=(5080)-333=174kN-m101Mau(5080)167=-675kN-m10Foac =100kN3■支座移动(79400)=95.2kNFNBD2500■温度变化（7）作内力图RAKAF95.2100Fr-95.358242.8mamdanFaugmon1740241100F(单位kN)M图（单位kNm）F图（单位kN)PA8

8 作图示结构內力图。吊杆的EA等于横梁EI的1/20m2。 解 （2）基本未知量 取结点B的转角θ和竖向 位移 Δ为基本未知量。 （1）半边结构 （3）固端力2 2 F 2 2 F 10 10 333kN m 3 3 10 10 167kN m 6 6 BC CB ql M ql M × =− =− =− ⋅ × =− =− =− ⋅ 半边结构 基本体系 F Q F Q 10 10 100kN 0 BC CB F ql F ==×= = （4）求杆端力 杆AB 2 2 6 26 2 20 20 6 46 4 20 20 6 12 AB AB AB BA AB AB EI EI Mi i l EI EI Mi i l M M EI EI Δ θ θ Δ Δ θ θ Δ =− = − =− = − + Q 2 3 6 12 20 20 AB AB BA M M EI EI F l θ Δ + = − =− + 杆BC Q F F F Q 333 10 167 10 BC 100 BC AB BC CB AB CB BC EI Mi M EI M iM F F θ θ θ θ =+ = − =− + = − = = 杆BD N 3 3 20 5 25 5 3 3 5 20 25 2500 BD EI EA F l EI EI Δ Δ Δ Δ ⎛⎞ ⎛⎞ = =− ⎜⎟ ⎜⎟ ⎝⎠ ⎝⎠ = = × × （5）列位移法方程 考虑B点平衡 0, 0 ∑ M MM B BA BC = += NQQ 3 0, 0 5 ∑ F FFF y Bd BA Bc = +−= （5）最终杆端力 333 0.3 0.015 100 0.015 0.00222 EI EI θ Δ θ Δ ⎫ − = ⎪⎪ ⎬ ⎪ −+ = ⎪⎭ 5080 79400 EI EI θ Δ = = （ ）最终杆端力 ( ) ( ) ( ) ( ) ( ) ( ) 2 2 Q 2 3 2 6 5080 79400 682kN m 20 20 4 6 5080 79400 174kN m 20 20 6 12 5080 79400 42.8kN 20 20 AB BA BC M M F = − =− ⋅ = − =− ⋅ =− + = ( ) ( ) Q 1 5080 333 174kN m 10 1 5080 167 675kN m 10 100kN BC BA BC M M F = −= ⋅ = − =− ⋅ = N ( ) 3 79400 95.2kN 2500 F BD = = （7）作內力图 2500 7-7 支座移动和温度改变时的计算 „ 支座移动 „ 温度变化

示例1支座位移时的计算作图示连续梁支座C下沉4.时的弯矩图超静定结构当支座产生位移时，结构中一股会引起内力。用位移法计算时，基本未知量和基吊本方程以及作题步骤都与荷载作用时一样，不同F的只有固端力一项，例如由荷载作用产生的固端解（1）基本未知量6：弯矩改变成由已知位移作用产生的“固端弯矩”。（2）求杆端弯矩Ma =310 Mc =3i0g-3/4（3）列位移法方程2温度改变时的计算ZM,=0610,-3/午=0~%-Mga +Mac. =0"271■温度改变时的计算，与支座位移时的计算基本相同。（4）最终杆端弯矩■杆件内外温差使杆件弯曲，产生固端弯矩。(14)=1.514■温度改变时杆件的轴向变形使结点产生已知位移Mu=3(21使杆端产生相对横向位移，又产生另一部分“固端弯(14)-3年=-1.54M sc = 3i|矩”，21J1514e9B示例作刚架由于温度改变所产生的弯矩。各杆截面尺寸相同。排架由于温度均匀升高t所产生的弯矩。0.4mE1,--30CD182.00-7-4=10c,=10'cgLOT.ID6.m/=6m←解（1）半边结构解△=αtLgm-30cM=-3/4--3,atlL为结点到2基本未知量：4-10℃对称轴距离h/=6 m9

9 超静定结构当支座产生位移时，结构中一般 会引起内力。用位移法计算时，基本未知量和基 本方程以及作题步骤都与荷载作用时一样，不同 1 支座位移时的计算 本方程以及作题步骤都与荷载作用时 样 的只有固端力一项，例如由荷载作用产生的固端 弯矩改变成由已知位移作用产生的“固端弯矩”。 作图示连续梁支座C下沉ΔC时的弯矩图。 示例 解（1）基本未知量θB （2）求杆端弯矩 3 33 C MBA B BC B iM i i l Δ = =− θ θ （3）列位移法方程 （4）最终杆端弯矩 0 0 B BA BC M M M = + = ∑ 63 0 C B i i l Δ θ − = 1 2 C B l Δ θ = 1 3 15 Mi i ⎛ ⎞ Δ Δ C C = = ⎜ ⎟ 3 1.5 2 1 3 3 1.5 2 BA CC C BC Mi i l l M i ii ll l ΔΔ Δ = = ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ = − =− ⎜ ⎟ ⎝ ⎠ ■ 温度改变时的计算，与支座位移时的计算基本相同。 ■ 杆件内外温差使杆件弯曲，产生固端弯矩。 ■ 温度改变时杆件的轴向变形使结点产生已知位移， 2 温度改变时的计算 温度改变时杆件的轴向变形使结点产 已知位移 使杆端产生相对横向位移，又产生另一部分“固端弯 矩”。 排架由于 温度均匀升高 t 所产生的弯矩。 示例 解 L为结点到 对称轴距离 Δ α= tL 3 3 tL Mi i h h Δ α =− =− 作刚架由于 温度改变所产生的弯矩。各杆截面尺寸相同。 解 （1）半边结构 基本未知量θB

（2）求杆端弯矩<各杆的相对横向位移：杆端弯矩A=A8c=60α0EIMAB=2iAOg+MIB=20g+(-22.5αEI66.7αEI)4aB4Bc =4l-4lc =-80α4--10℃=0.5EI0g89.2αEI各杆的固端弯矩t--10c/t-10℃ 10℃10℃Ma=4iam0g+Mi=4El0M- Mi --64n --25αEI0g+(-22.5αEI+66.7αEI)4aDLH=1.0E10g+44.2αEI轴向温度变化引起的Mc = M =-6=4sc =13.3αEIMg=4ig0g+M=4El0固端弯矩0 +(13.3αEI-66.7aEI)46■两侧温度差产生固端弯矩各杆的轴向变形=0.67EI0,53.3αEIElα=66.7αEl-M=M-5N=αt,H = -40αMa=2ig-0,+Mog-2号0h-0g+(13.3αEI+66.7αEI)4aBAlcp =αt.H= 40αEla=0.33EI0g+80.0αEI-MBc = McB == 66.7αEIAc=αt,/=60αh小结（3）列位移法方程Mm+Msc=01.67EI0,9.1αEI=000g=5.4α■形常数与载常数表（转角位移方程）（4）最终杆端弯矩■直接平衡法与基本体系法步骤Ma =(0.5×5.4-89.2)αEI = 86.5αEI（1）取基本未知量（1）取位移法基本体系（2）列杆端弯矩计算式（2）建立位移法方程Ma(5.4+44.2)αEI = 49.6αEI（3）建立位移法基本方程（3）求系数和自由项M nc =(0.67×5.4-53.3)αEI =49.7αEI（4）解方程（组）（4）解方程（组）Mc=(0.33×5.4+80.0)αEl=81.8αEI（6）算杆端弯矩作弯矩图（5）叠加作弯矩图81.8aEl■对称性应用一取半边结构49.6aEl（5）画弯矩图■支座移动和温度变化一一广义固端弯矩三MI最少基本未知量与基本结构具86.5aE/4DL作业7-2b/d、7-5无侧移刚架》下一章内容7-7、7-10有侧移刚架第2章结构的几何构造分析7-12、7-14对称性10

10 （2）求杆端弯矩 ▲各杆的相对横向位移： 60 80 AB BC BC AB BC l l l ΔΔ α ΔΔ Δ α = = = − =− F F 6 22.5 AB BA AB i M M EI H i = =− =− Δ α ▲各杆的固端弯矩 0 40 AB Δα α l tH = =− 0 40 CD Δα α l tH = = 0 60 BC Δα α l tl = = ▲各杆的轴向变形 F F 6 13.3 BC CB BC i M M EI l = =− = Δ α ■轴向温度变化引起的 固端弯矩 ■两侧温度差产生固端弯矩 F F F F 66.7 66.7 AB BA BC CB EI t M M EI h EI t M M EI h αΔ α αΔ α −= = = −= = = 杆端弯矩 ( ) ( ) F F 2 2 22.5 66.7 4 0.5 89.2 4 4 22.5 66.7 4 1 0 44 2 AB AB B AB B AB B BA AB B BA B AB EI M i M EI EI EI EI EI M i M EI EI EI EI θ θ α αΔ θ α θ θ α αΔ θ α = + = +− − = − = + = +− + = + ( ) F F 1.0 44.2 4 4 13.3 66.7 6 0.67 53.3 2 2 13. 6 B BC BC B BC B AB B CB BC B CB B EI EI EI M i M EI EI EI EI EI Mi M θ α θ θ α αΔ θ α θ θ = + = += + − = − = += + ( ) 3 66.7 0.33 80.0 AB B EI EI EI EI α αΔ θ α + = + （3）列位移法方程 （4）最终杆端弯矩 0 M M BA BC + = 1.67 9.1 0 EI EI θ α B − = 5.4 θ B = α ( ) ( ) 0.5 5.4 89.2 86.5 5.4 44.2 49.6 AB BA M EI EI M EI EI α α α α = × − =− =+ = （5）画弯矩图 ( ) ( ) 0.67 5.4 53.3 49.7 0.33 5.4 80.0 81.8 BC CB M EI EI M EI EI α α α α = × − =− = ×+ = 小 结 （1）取基本未知量 （2）列杆端弯矩计算式 （3）建立位移法基本方程 „ 形常数与载常数表（转角位移方程） „ 直接平衡法与基本体系法步骤 （1）取位移法基本体系 （2）建立位移法方程 （3）建立位移法基本方程 （3）求系数和自由项 （4）解方程（组） （6）算杆端弯矩作弯矩图 „ 对称性应用——取半边结构 „ 支座移动和温度变化——广义固端弯矩 „ 最少基本未知量与基本结构 （3）求系数和自由项 （4）解方程（组） （5）叠加作弯矩图 作 业 7-2b/d、7-5 无侧移刚架 7-7、7-10 有侧移刚架 7-12、7-14 对称性 ¾ 下一章内容 第 2 章 结构的几何构造分析