《结构力学》课程教学资源（课件讲稿）第五章 结构的位移计算

2013-6-25第5章虚功原理和结构位移计算教学目标：第5章虚功原理和结构位移计算■了解互等定理；Virtual WorkPrinciple and Calculation of■掌握荷载作用下静定结构位移计算方法（图乘法）；静定结构因温度改变和支座移动所引起Displacement of Structures的位移计算；理解功、虚功和变形体虚功原理的基本概念。5-1应用虚力原理求刚体体系的位移第5章虚功原理和结构位移计算教学要求：教学内容：■了解位移的概念。5.1应用虚力原理求刚体体系的位移■掌握刚体体系位移计算的方法。5.2变形体的虚功原理和结构位移计算的一般公式■理解虚力原理的概念。5.3/4荷载下结构的位移计算和举例（积分法）主要内容：5.5图乘法■结构位移概述5.6温度作用时的位移计算■刚体体系的位移计算5.7互等定理■小结25-1应用虚力原理求刚体体系的位移5-1应用虚力原理求刚体体系的位移1.结构位移概述1.结构位移概述成都居民楼雨后倾斜塔科马大桥风振破坏上海莲花13层倒楼

2013-6-25 1 第5章 虚功原理和结构位移计算 Virtual Work Principle and Calculation of Displacement of Structures 教学目标： 第 5 章 虚功原理和结构位移计算 „ 了解互等定理； „ 掌握荷载作用下静定结构位移计算方法（图乘 法）；静定结构因温度改变和支座移动所引起 的位移计算； „ 理解功、虚功和变形体虚功原理的基本概念。 教学内容： 第 5 章 虚功原理和结构位移计算 5.1 应用虚力原理求刚体体系的位移 5.2 变形体的虚功原理和结构位移计算的一般公式 5.3/4 荷载下结构的位移计算和举例（积分法 ） 5.5 图乘法 5.6 温度作用时的位移计算 5.7 互等定理 教学要求： 5-1 应用虚力原理求刚体体系的位移 „ 了解位移的概念。 „ 掌握刚体体系位移计算的方法。 „ 理解虚力原理的概念 主要内容： 。 „ 结构位移概述 „ 刚体体系的位移计算 „ 小结 1. 结构位移概述 5-1 应用虚力原理求刚体体系的位移 上海莲花13层倒楼 5-1 应用虚力原理求刚体体系的位移 1. 结构位移概述 成都居民楼雨后倾斜 塔科马大桥风振破坏

2013-6-255-1应用虚力原理求刚体体系的位移1.结构位移概述5-1应用虚力原理求刚体体系的位移1.结构位移概述P》产生位移的原因荷载作用DAR.N荷载变形体位移777支座沉降温度变化、制造误差支座移动DB_-i-》计算位移的目的刚体位移C7刚度验算超静定结构分析结构各点产生位移时，结构内部。地震作用下铁路破坏思考是否产生应变？5-1应用虚力原理求刚体体系的位移5-1应用虚力原理求刚体体系的位移2.刚体体系的位移计算2.刚体体系的位移计算>刚体体系虚功原理应用的回顾问题BA平衡的力状态CT（实际）TTATF,-?4B1协调的位移状态手段：刚体体系虚功原理（虚设）TT7具有理想约束的刚体体系：AAL设体系上作用任意的平衡力系。又设体系发生符-F-Ac+(-F-△,)=0虚位移原理虚功方程：合约束条件的微小刚体体系位移，则外力在位移上（联想：如果问题反过来，不是求力，所作的虚功总和恒等于零。而是求位移该如何运用虚功原理解决？）5-1应用虚力原理求刚体体系的位移2.刚体体系的位移计算5-1应用虚力原理求刚体体系的位移2.刚体体系的位移计算FA=?DAB平衡的力状态D+B（虚设）C7.TFAAc=?3gDNB-T--协调的位移状态（实际）zC7.7AAALTIT列出虚功方程：-F.c+(-F△,)=0虚力原理TFAsIFp为了便于计算：令F=1单位荷载法虚功方程-1-Ac+(-FA)=0→Ac=A,/32

2013-6-25 2 5-1 应用虚力原理求刚体体系的位移 1. 结构位移概述 ¾ 产生位移的原因 荷载 支座沉降 温度变化、制造误差 地震作用下铁路破坏 ¾ 计算位移的目的 刚度验算 超静定结构分析 A B D 支座移动 变形体位移 荷载作用 A B C D P 5-1 应用虚力原理求刚体体系的位移 1. 结构位移概述 结构各点产生位移时，结构内部 是否产生应变？ Δ 思考 刚体位移 A B C D 支座移动 2. 刚体体系的位移计算 问题： Δ ？ A B C D 5-1 应用虚力原理求刚体体系的位移 手段： 刚体体系虚功原理 具有理想约束的刚体体系： 设体系上作用任意的平衡力系。又设体系发生符 合约束条件的微小刚体体系位移，则外力在位移上 所作的虚功总和恒等于零。 ¾ 刚体体系虚功原理应用的回顾 平衡的力状态 （实际） F FAy＝？ ΔC A B C D 5-1 应用虚力原理求刚体体系的位移 2. 刚体体系的位移计算 A B C D 协调的位移状态 （虚设） ΔA ΔC 虚功方程： （联想：如果问题反过来，不是求力， 而是求位移该如何运用虚功原理解决？） ( ) 0 −F F C Ay A ⋅Δ + − ⋅Δ = 虚位移原理 平衡的力状态 （虚设） A B C D F FAy 协调的位移状态 A B D ΔC=？ 5-1 应用虚力原理求刚体体系的位移 2. 刚体体系的位移计算 （实际） C ΔA 列出虚功方程： ( ) 0 − ⋅Δ + − ⋅Δ = F F C Ay A 虚力原理 为了便于计算： 令 F =1 单位荷载法 ΔA A B C D ΔC=？ 3a a 2a 5-1 应用虚力原理求刚体体系的位移 2. 刚体体系的位移计算 虚功方程 −1 0 ⋅Δ + − ⋅Δ = C Ay A ( F ) / 3 ⇒Δ =Δ C A A B C D FAy FBy FDy 1 FDx

2013-6-255-1应用虚力原理求刚体体系的位移2.刚体体系的位移计算5-1应用虚力原理求刚体体系的位移2.刚体体系的位移计算（3）若广义力是等值、反向的一对力F。》广义力与广义位移★FF+作功的两方面因素：广义力、广义位移。ABBAa广义力F：与力有关的因素。A4AB：AB两点的相对位移。广义位移4：与位移有关的因素。虚功：W=F4（4）若广义力是一对等值、反向的力偶M9（1）广义力是一个力，广义位移是力作用方向上的位移。MBOM1（2）广义力是一个力偶，广义位移是力偶作用截面的转角OAB：AB两截面的相对转角。5-1应用虚力原理求刚体体系的位移示例5-1应用虚力原理求刚体体系的位移示例B--BT-C0er3a23a2aaJBWD数学方法.T.TTFNFByFpr虚功方程1.Ccp+(-FA)=0=0cp.6a5-1应用虚力原理求刚体体系的位移示例5-1应用虚力原理求刚体体系的位移示例（1）B点的水平位移>虚设单位荷载例：已知C支座产生水平向右位移5cm和竖直向下位RB移2cm，求B点的水平位移和BC杆的转角。R5clFcl2cm2m / 2m|TF15c CIRF!2cm位移状态虚设平衡力状态7.2m2m>建立虚功方程>解方程位移状态虚设平衡力状态1×+(-Fg×2)+F×5=0=H=4.5cm3

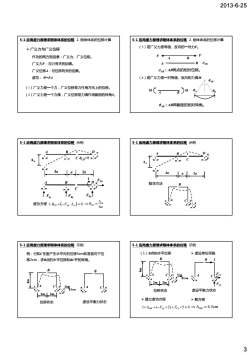
2013-6-25 3 ¾ 广义力与广义位移 作功的两方面因素：广义力、广义位移。 广义力F：与力有关的因素。 广义位移Δ：与位移有关的因素。 5-1 应用虚力原理求刚体体系的位移 2. 刚体体系的位移计算 （1）广义力是一个力，广义位移是力作用方向上的位移。 （2）广义力是一个力偶，广义位移是力偶作用截面的转角θ。 虚功： W=FΔ （3）若广义力是等值、反向的一对力F。 F F A B ΔAB：AB两点的相对位移。 A B ΔAB 5-1 应用虚力原理求刚体体系的位移 2. 刚体体系的位移计算 （4）若广义力是一对等值、反向的力偶M θAB：AB两截面的相对转角。 θAB M A B M θA θB ΔA A B C D θCD=？ 3a a 2a 5-1 应用虚力原理求刚体体系的位移 示例 虚功方程 1 0 ⋅ + − ⋅Δ = θ CD Ay A ( ) F 6 A CD a θ Δ ⇒ = A B C D FAy FBy FDy 1 FDx ΔA A B C D 3a a 2a 5-1 应用虚力原理求刚体体系的位移 示例 数学方法 B A C B m B 例：已知C支座产生水平向右位移5cm和竖直向下位 移2cm，求B点的水平位移和BC杆的转角。 5-1 应用虚力原理求刚体体系的位移 示例 A C 2m 4m 2m 5cm 2cm A C 位移状态 虚设平衡力状态 B A C 4m 5cm 2cm B A C 1 FCx （1）B点的水平位移 ¾ 虚设单位荷载 5-1 应用虚力原理求刚体体系的位移 示例 2m 2m 位移状态 虚设平衡力状态 FCy 1 ( 2) 5 0 ×Δ +− × + × = BH Cy Cx F F 4.5 BH ⇒Δ = cm ¾ 建立虚功方程 ¾ 解方程

2013-6-255-1应用虚力原理求刚体体系的位移示例5-1应用虚力原理求刚体体系的位移（2）BC杆的转角》虚设单位荷载求B、C两点的相对线位移。课常练习：BMBSC元E1T2m/2mN虚设平衡力状态位移状态2m2mFoy虚设平衡力状态位移状态>建立虚功方程>解方程1×0Bc+(-Fc,×2)+Fα×5=0=0c=S5-1应用虚力原理求刚体体系的位移小结5-2变形体的虚功原理和结构位移计算的一般公式应用虚力原理求支座移动时刚体体系的位移（1）局部变形时的位移计算公式单位荷载法基本思路：在刚性杆中，取微段ds设为变形体，分析局部变形所引起的位移。（1）沿所求位移方向虚设单位荷载，D求相应的支座反力：asdstdr（2）建立虚功方程1-△+RA,=0（3）解方程得A=-ZRA,25-2变形体的虚功原理和结构位移计算的一般公式5-2变形体的虚功原理和结构位移计算的一般公式sds1产-tdn微段两端截面Idn的相对位移RN0Mdededo=xdsd=edsdn=yodsoodsM,ESN.X=A2FR-EIEAd=edsGAdn=odsd4=(M+Ng+0.)dsN.(2)结构位移计算的一般公式M=材料力学：E=KGAETEAC4=EIEAGA4

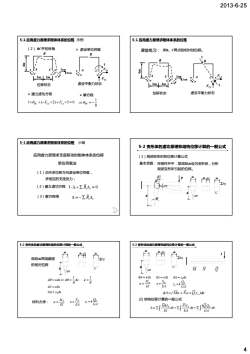
2013-6-25 4 B A C 4m 5cm 2cm FCx B A C ¾ 虚设单位荷载 1 （2） BC杆的转角 5-1 应用虚力原理求刚体体系的位移 示例 2m 2m 位移状态 FCy ¾ 解方程 虚设平衡力状态 1 8 ⇒ =− θ BC 1 ( 2) 5 0 × +− × + × = θ BC Cy Cx F F ¾ 建立虚功方程 B 4m B 课堂练习： 求B、C两点的相对线位移。 1 5-1 应用虚力原理求刚体体系的位移 A C 2m 2m 5cm 2cm A C 位移状态 虚设平衡力状态 FCy FCx 1 小结 单位荷载法 （1）沿所求位移方向虚设单位荷载， 应用虚力原理求支座移动时刚体体系的位移 5-1 应用虚力原理求刚体体系的位移 求相应的支座反力； （3）解方程得 （2）建立虚功方程 1 0 Ri i ⋅Δ+∑ Δ = Δ =−∑ Δ Ri i （1）局部变形时的位移计算公式 基本思路： dλ ds 在刚性杆中，取微段ds设为变形体，分析 局部变形所引起的位移。 P 5-2 变形体的虚功原理和结构位移计算的一般公式 ds dλ dη dθ R ds dλ ds dη dθ R D γ ds P ds dλ ds dη dθ R D γ ds 1 1 d dd d θκ θ κ = ⇐= = s s 微段ds两端截面 的相对位移 5-2 变形体的虚功原理和结构位移计算的一般公式 材料力学： EI MP κ = EA NP ε = GA Qk P γ D = 0 d dd d d d d d s s R R s s θκ θ κ λ ε η γ = ⇐= = = = M N Q ds dλ ds dη dθ R D γ ds 1 0 d dd dd d θ = κ λε s = = s s η γ 5-2 变形体的虚功原理和结构位移计算的一般公式 EI MP κ = EA NP ε = GA Qk P γ D = (2) 结构位移计算的一般公式 d ( M N Q )ds D Δ = κ + ε + γ ∫ ∫ ∫ = ∑ + ∑ + ∑ ds GA kQQ ds EA NN ds EI MMP P P Δ

2013-6-255-2变形体的虚功原理和结构位移计算的一般公式5-3/4荷载下结构的位移计算和举例(3）位移计算公式也是变形体虚功原理的一种表达式。线性弹性材料变形体虚功原理：各微段内力在应变上所作的内虚功总++[4=和等于荷载在位移上以及支座反力在支座位移上所作的EIJEAJGA外虚功总和，即：N.Q,,M，实际荷载引起的内力N.O,M虚设单位荷载引起的内力MMeds+ZJ[d+Jrds1XA+RC,=ZJEIEAGA正负号规定外虚功内虚功N,N,以拉为正0.0,使微段顺时针转动为正M,M，当M与M,使杆件同侧纤维受拉乘积为正25-3/4荷载下结构的位移计算和举例5-3/4荷载下结构的位移计算和举例-x例1:求悬臂梁在A端的竖向位移△，并比较弯曲变形与剪切MM.ql弯曲典：4=Eds=E8F变形对位移的影响。设梁的截面为矩形。 -12 -06qlq剪切：4,-解：虚设单位荷载GAGAGA实际荷载虚设单位荷载AXI设 μ=1/3,E/G =2(1+μ)=3/8M,=-1gr=-x矩形载面1/A=h/120, =-1Q, =-gx[P=]40.6g/N=0N,=004=4.8EL2=1.07GAR-4qf(-x)MM,-3r8EIql弯曲变形位移A=dx=EI8E浅梁h/1=1/10A,/A,=1.07%可忽略剪切变形位移koe.ds=1.2[(-1)(-9g),x=0.69l(矩形截面，k=1.2)A,=深梁h/=1/2A/A,=26.75%不可忽略JGAGA5-3/4荷载下结构的位移计算和举例示例5-3/4荷载下结构的位移计算和举例示例例3：图(a)所示为一等截面圆弧形曲杆4B，截面为矩形，圆弧例2：计算结点D的竖向位移。各杆E4相同且为常数。AB的圆心角为α，半径为R。试求B点的竖向位移4.[P+C解：虚设荷载解：-0.7P(a)M=XM,=-5gr0-NN图(b) Fv=sing0.5P图(a) Fau =-qrsineR4.=ZFo=cos0dDFoe=qxcosodEA--10.5P10.5P4=93EI2EI:Pd0.7(0.7×1.4+0.52×1)×22qR(b)5d-Re2c05a+1cos a) α=90 Aw=AA=)EAE33EAB0.5FFads-kgxakqr(lcos αa)A0"3GAAo=1.87PdID4-茶-JaGAGAEA1+401110.5Ax0.5设h/R=1/3，EIG=8/3，IIA=h2/12A3756005

2013-6-25 5 (3) 位移计算公式也是变形体虚功原理的一种表达式。 变形体虚功原理：各微段内力在应变上所作的内虚功总 和等于荷载在位移上以及支座反力在支座位移上所作的 外虚功总和。即： 5-2 变形体的虚功原理和结构位移计算的一般公式 外虚功 内虚功 ∑ ∫ ∫ ∫ ×Δ + = ∑ + ∑ + ∑ ds GA kQQ ds EA NN ds EI MM R c P P P k 1 k 线性弹性材料 ∫ ∫ ∫ = ∑ + ∑ + ∑ ds GA kQQ ds EA NN ds EI MMP P P Δ , , Npp p Q M 实际荷载引起的内力 5-3/4 荷载下结构的位移计算和举例 当 与 使杆件同侧纤维受拉乘积为正 M M p N, , Q M 虚设单位荷载引起的内力 正负号规定 N,Np 以拉为正 , Q Qp 使微段顺时针转动为正 , M M p 例1:求悬臂梁在A端的竖向位移Δ，并比较弯曲变形与剪切 变形对位移的影响。设梁的截面为矩形。 A x l q 解: 虚设单位荷载 实际荷载 虚设单位荷载 1 2 2 M p = − qx M = −x 5-3/4 荷载下结构的位移计算和举例 A x P=1 Q qx p = − 1 Qp = − 0 Np = N = 0 弯曲变形位移 ( ) 2 4 1 0 1 2 8 l p x qx MM ql ds dx EI EI EI ⎛ ⎞ − −⎜ ⎟ ⎝ ⎠ Δ= = = ∫ ∫ 剪切变形位移 (矩形截面，k=1.2) ( )( ) 2 2 0 1 1.2 0.6 l p kQQ qx ql ds dx GA GA GA − − Δ= = = ∫ ∫ 设 μ =1 3, 2 1 3 8 E G = += ( ) μ 矩形截面 2 IA h 12 5-3/4 荷载下结构的位移计算和举例 弯曲: ( ) 2 4 1 0 1 2 8 l p x qx MM ql ds dx EI EI EI ⎛ ⎞ − −⎜ ⎟ ⎝ ⎠ Δ= = = ∫ ∫ 剪切: ( )( ) 2 2 0 1 1.2 0.6 l p kQQ qx ql ds dx GA GA GA − − Δ= = = ∫ ∫ 2 2 4 2 1 0.6 4.8 8 ql GA EI ql GAl EI Δ = = Δ 矩形截面 2 IA h = 12 2 2 1 1.07 h l Δ ⎛ ⎞ = ⎜ ⎟ Δ ⎝ ⎠ 浅梁 h l =1 10 2 1 Δ Δ =1.07% 可忽略 深梁 h l =1 2 2 1 Δ Δ = 26.75% 不可忽略 例2：计算结点D的竖向位移。各杆EA相同且为常数。 P A B C D -0.7P 解： d d d 0 0.5P EA NN l P ΔC = ∑ 5-3/4 荷载下结构的位移计算和举例 示例 C A B D 1 0.5P 0.5P 0.5 0.5 -0.7 1 0.5 EA ( ) 0.7 1.4 0.5 1 2 2 2 = × + × × EA Pd EA 1.87Pd = 例3：图(a)所示为一等截面圆弧形曲杆AB，截面为矩形，圆弧 AB的圆心角为α，半径为R。试求B点的竖向位移△。 解：虚设荷载 图(a) θ θ cos sin 2 1 QP NP 2 P F qx F qx M qx = = − = − 图(b) θ θ cos sin Q N = = − = − F F M x 5-3/4 荷载下结构的位移计算和举例 示例 QP q ∫ ∫ ∫ Δ = = × − Δ = = − + Δ = = − + A B A B A B GA kqR s GA kF F EA qR s EA F F EI qR s EI M M (1 cos ) 3 1 d cos ) 3 1 cos 3 2 d ( cos ) 3 1 cos 3 2 ( 2 d 3 2 QP Q Q 3 2 NP N N 3 4 P M α α α α α D α =90 GA kqR EA qR EI qR 3 3 2 3 2 Q 2 N 4 M Δ = Δ = Δ = 设h/R=1/3，E/G=8/3，I/A=h2/12 600 1 M N = Δ Δ 375 1 M Q = Δ Δ

2013-6-255-3/4荷载下结构的位移计算和举例，示例5-3/4荷载下结构的位移计算和举例，小结MM,NN,rkerds例4：求简支梁两端截面4、B的相对转角4。4=>-ds+>ds+>JEAEIGA1,MMeds解：虚设力系（a）梁与刚架4=EIM=1 (0图乘的一般方法常见图形的面积和形心的位置例1求图示结构B点的竖向位移/P1/2质点12A,0(b+0/3(a+1/3ATB二次抛物线A=2hl/3LA=hl/2顶点M.-1顶点A=--AyYEI31/41/451/8+31/8M二次抛物线A=hl/3二次抛物线A=2hl/3（1）两图均是直线图形6

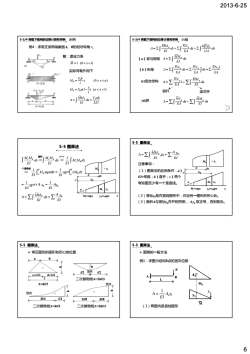
2013-6-25 6 例4：求简支梁两端截面A、B的相对转角△。 解：虚设力系 实际荷载作用下 M =1 (0 ) < <x l 5-3/4 荷载下结构的位移计算和举例 示例 P P P P (0 ) (1 ) ( ) F b M x xa l x M Fa a x l l = < < = − << 2 MM F ab P P ds EI EI Δ= = ∫ ∫ ∫ ∫ = ∑ + ∑ + ∑ ds GA kQQ ds EA NN ds EI MMP P P Δ （a）梁与刚架 ∫ = ∑ ds EI MMP Δ （b）桁架 EA NN l ds EA NN ds EA NNP P P = ∑ = ∑ =∑ ∫ ∫ Δ 5-3/4 荷载下结构的位移计算和举例 小结 (c)组合结构 NN MM p p l ds EA EI Δ= + ∑ ∑∫ (d)拱 NN MM p p ds ds EA EI Δ= + ∑ ∑ ∫ ∫ 链杆 梁式杆 ∫ i k ds EI M M ⇒ ∫ = i k EI C M M dx EI 1 ∫ = B A tg xMkdx EI 1 α ⇒ ∫ B A k M M xtg dx EI i 1 α 是直线 ⇒∫ i k dx EI 直杆 M M Mk dx x A 5-5 图乘法 Δ = ∑∫ P = ∑ EI y dx EI MM Α 0 = y EI 0 1 = tg × x Α EI 0 1 α Α α Mi Mi =xtgα y x y0 x0 y0=x0tgα Δ = ∑∫ P = ∑ EI y dx EI MM Α 0 注意事项： （1）图乘法的应用条件：a） EI=常数；b）直杆；c）两个 y Mk dx x x0 A 5-5 图乘法 EI=常数；b）直杆；c）两个 弯矩图至少有一个是直线。 （2）竖标y0取在直线图形中，对应另一图形的形心处。 （3）面积A与竖标y0在杆的同侧， A y0 取正号，否则取负。 α Mi Mi =xtgα x y0 y0=x0tgα ¾ 常见图形的面积和形心的位置 (a+l)/3 (b+l)/3 l a b h l/2 l/2 h 二次抛物线A=2hl/3 顶点 5-5 图乘法 A=hl/2 二次抛物线A 2hl/3 h 3l/4 l/4 5l/8 3l/8 二次抛物线A=hl/3 二次抛物线A=2hl/3 h 顶点 顶点 ¾ 图乘的一般方法 A B L P 例1：求图示结构B点的竖向位移 A1 5-5 图乘法 （1）两图均是直线图形 L y1 1 1 1 A y EI Δ = MP M 1

2013-6-255-5图乘法5-5图乘法例3：求图示结构B点的转角例2：求图示结构C点的竖向位移M,9M,7MA10042M,M2AqL2/89BTLAM(11L2kL2益BYAT1M*△=(Ay,+Ay2)Y3E)M（2）分段图乘一图形为曲线，另外一图形为折线5-5图乘法5-5图乘法，示例回顾M,弯矩图绘制方法·叠加法例1：求B点和C点的竖向位移，EI为常数P410M,M2(1)计算B点的竖向位移1+M,ATB.1CL/2A2 9L/2个Au,yA=qL2/8M,++EMr+PL$xLxPLx2L-P11As0M.AE/2NEI3&AT1Mp△=(Ay+A-A)LEI↓-MBAM（3）分块图乘YY3y25-5图乘法，示例5-5图乘法，示例（2）计算C点的竖向位移例2：求图示刚架C点的水向位移，EI为常数。方法2：错误方法1：LA,qL2/2Ly1PLrPLCDTY2J1942A2oBA2BATL19L-/8Mp/y3Mp1A31→L/2L2AB MMpCMCTA1MT2111115PL3134=4,<Ix--qA=XLX万=元Ac=AyPL:Lx=L×-82EIEI2248EI26_3qL1不等？(, +A+Ay)1PLAc118EIAc=EAy2×L×PLxEI12EIEI 22327

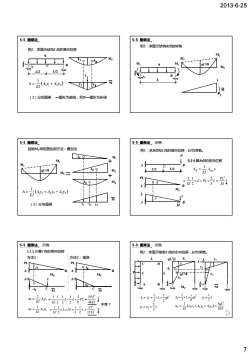
2013-6-25 7 q 例2：求图示结构C点的竖向位移 A B L/2 L/2 C A1 A2 MP 5-5 图乘法 （2）分段图乘 一图形为曲线，另外一图形为折线 y1 y2 ( ) 1 1 2 2 1 A y A y EI Δ = + M 1 q 例3：求图示结构B点的转角 M1 M2 MP M1 M2 qL2/8 5-5 图乘法 A B L M 1 1 回顾MP弯矩图绘制方法－叠加法 A1 A2 MP M1 M2 qL2/8 M1 M2 5-5 图乘法 y1 y2 A3 y3 Mq M （3）分块图乘 ( ) 1 1 2 2 3 3 1 A y A y A y EI Δ = + − 例1：求B点和C点的竖向位移，EI为常数。 P L/2 L/2 A B C PL A y EI B M P 1 Δ = 3 1 1 2 （1）计算B点的竖向位移 5-5 图乘法 示例 A B PL MP A B L M EI PL L PL L EI 3 3 2 2 1 1 = × × × = A y 1 A B PL MP 方法1： y1 （2）计算C点的竖向位移 L/2 A B PL MP A2 L/2 方法2：错误 1 5-5 图乘法 示例 EI PL L L PL EI 48 5 6 5 2 1 2 1 2 1 1 3 1 1 = × × × = 1 A y EI Δc = A1 L/2 M C y2 L/2 M C 2 2 1 A y EI Δc = EI PL L PL L EI 2 12 1 3 1 2 1 1 3 = × × × × = 不等？ 1 例2：求图示刚架C点的水向位移，EI为常数。 q L C D L L qL2/2 L A1 y1 A2 y2 A3 qL y3 2/8 1 5-5 图乘法 示例 A B M ( ) EI qL A y A y A y EI C 8 1 3 4 Δ = 1 1 + 2 2 + 3 3 = MP 2 1 2 1 2 1 1 2 2 2 3 A A L qL yy L = = ×× = = 2 3 3 21 1 38 2 A = ×× = L qL y L

2013-6-255-6温度作用时的位移计算5-6温度作用时的位移计算at,dttat,ds=du》杆件温度变化时，静定结构不会引起内力+t但材料会发生膨胀和收缩，从而引起截面的应变，dsL使结构产生变形和位移。+atdsuS上边缘温度上升，上边缘温度上升t2。》温度沿截面厚度为线性分布，温度变形后，截面保持为平面。+BA>温度变形：重+t, 沿轴线方向拉伸变形du和截面转角do。ds5-6温度作用时的位移计算5-6温度作用时的位移计算，at,dst,d.（1)dur计算du=at.dsdu= eds=at,dst.ds=dt.ds=dudo-aids形心轴处的温度ht,h,+t,hat,dsat,ddsfo=t,温度作用引起的位移：A=-Za, Nds+[Mds当h,=h,时（+正负号规定：α(-t)ds_aAtdsdo=（2)d计算轴力N以拉为正：t以温度升高为正。hhM与引起的弯矩为同一方向时乘积为正；反之为负。5-6温度作用时的位移计算示例5-7互等定理例1.刚架内侧温度升高10℃，外侧温度不变，=0.00001，各杆为矩形截面，高h=40cm。求：C点的竖向位移Ac。应用条件：1）应力与应变成正比0/P-1CD+10口B2)变形是微小的。+106m0即：线弹性变形体系。1.M图6mTA解：（1)C点加单位竖向力P=1，并作内力图。M和N功的互等定理(2) 代公式计算 A-Zam Nas+Z%[ Mds■位移互等定理6=(4+)=(0+10)=5=10-0=10■反力互等定理-10Ac=3+α(a)=0.93cm+58

2013-6-25 8 ¾ 杆件温度变化时，静定结构不会引起内力 ¾ 但材料会发生膨胀和收缩，从而引起截面的应变， 使结构产生变形和位移。 5-6 温度作用时的位移计算 A B ds 1 +t 2 +t 上边缘温度上升t1，上边缘温度上升t2。 2 h ds 2 αt ds 1 αt ds dθ 0 αt ds=du 1t 2t h 1 A B h ds 1 +t 2 +t 5-6 温度作用时的位移计算 ¾ 温度沿截面厚度为线性分布， 温度变形后，截面保持为平面。 ¾ 温度变形： 沿轴线方向拉伸变形du和截面转角dθ。 形心轴处的温度 ( ) 1 12 21 0 1 21 h th t h tt tt h h + =+ − = 0 du ds t ds = = ε α （1）du计算 5-6 温度作用时的位移计算 2 h ds 2 αt ds 1 αt ds dθ 0 αt ds=du 1t 2t h 1 h 0 1 21 ( ) h h 当h1=h2时 0 12 ( ) 1 2 t tt = + (t t ds 2 1 ) tds d h h α α θ − Δ （2）dθ计算 = = 温度作用引起的位移： 5-6 温度作用时的位移计算 2 h ds 2 αt ds 1 αt ds dθ 0 αt ds=du 1t 2t h 1 0 h du t ds =α tds d h α θ Δ = 温度作用引起的位移： 0 t t Nds Mds h α α Δ Δ= + ∑ ∑ ∫ ∫ 正负号规定： 轴力 以拉为正；t N 0以温度升高为正。 M 与 引起的弯矩为同一方向时乘积为正；反之为负。 Δt 例1. 刚架内侧温度升高10℃，外侧温度不变，α=0.00001， 各杆为矩形截面，高h=40cm。求：C 点的竖向位移ΔC。 A B C 6m 0 0 +10 +10 6m 5-6 温度作用时的位移计算 示例 M 图 P=1 B A C a 6m A M 图 解:（1）C点加单位竖向力P=1，并作内力图。M和N Δ= − = t 10 0 10 （2）代公式计算 0 t t Nds Mds h α α Δ Δ= + ∑ ∑ ∫ ∫ ( ) 2 2 0 10 1 0.93 2 C a a t a cm h α α − ⎛ ⎞ Δ = + + − =− ⎜ ⎟ ⎝ ⎠ ( ) ( ) 0 12 1 1 0 10 5 2 2 t tt = += + = 应用条件：1) 应力与应变成正比; 2) 变形是微小的。 即:线弹性变形体系。 5-7 互等定理 „ 功的互等定理 „ 位移互等定理 „ 反力互等定理

2013-6-255-7互等定理,5-7互等定理(2)位移互等定理（1）功的互等定理在任一线性变形体系中，由荷载P,=1所引起的与荷任一线性变形体系中，状态①的外力在状态②的位载P,=1相应的位移影响系数82等于由荷载P,所引起的移上作的功W，等于状态②的外力在状态①的位移上作的与荷载P,相应的位移影响系数312。功W21。即：Wi2-W21IP;①A1PIP282L?A1P2ABIF:1F2@2A202=0215-7互等定理，5.作业(3)反力互等定理在任一线性变形体系中，由位移c,=1所引起的与位5-2、5-55刚体虚功原理移c,=1相应的反力影响系数r等于由位移c,所引起的与5-9积分法求位移位移c,相应的反力影响系数12.5-11桁架位移证仅用于超静定结构5-17、19、22图乘法A.5S5-30、32温度作用下[Ri05A中TR21 R2ri2=r21M>下一章内容第6章力法9

2013-6-25 9 （1）功的互等定理 任一线性变形体系中，状态①的外力在状态②的位 移上作的功W12等于状态②的外力在状态①的位移上作的 功W21。即： W12= W21 5-7 互等定理 P1 P2 ① F1 F2 ② (2) 位移互等定理 P1 ① 在任一线性变形体系中，由荷载P1=1所引起的与荷 载P2=1相应的位移影响系数δ21 等于由荷载P2所引起的 与荷载P1相应的位移影响系数δ12 。 5-7 互等定理 ① P2 ② ⊗21 ⊗12 δ 12 = δ 21 (3)反力互等定理 c1 在任一线性变形体系中，由位移c1=1所引起的与位 移c2=1相应的反力影响系数r21 等于由位移c2所引起的与 位移c1相应的反力影响系数r12 。 仅用于超静定结构 5-7 互等定理 c c2 R11 R21 R12 R22 12 21 r = r 5. 作业 5-2、5-5 刚体虚功原理 5-9 积分法求位移 5-11 桁架位移 5-17、19、22 图乘法 5-30、32 温度作用下 ¾ 下一章内容 第 6 章 力法