《结构力学》课程授课教案（讲义）第三章 静定结构的受力分析 3.3 静定平面刚架

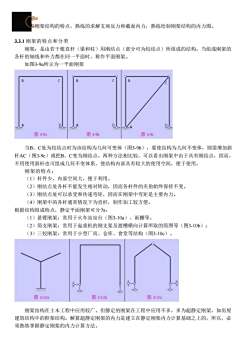
k量刚架结构的特点，熟练的求解支座反力和截面内力，熟练绘制刚架结构的内力图。3.3.1刚架的特点和分类刚架：是由若干根直杆（梁和柱）用刚结点（部分可为铰结点）所组成的结构。当组成刚架的各杆的轴线和外力都在同一平面时，称作平面刚架。如图3-9a所示为一平面刚架BB-.DD1A-图396图39℃图39a当B、C处为铰结点时为该结构为几何可变体（图3-9b），要使结构为几何不变体，则需增加斜杆AC（图3-9c）或把B、C变为刚结点。两种方法相比较，可以看出刚架中由于具有刚结点，因而，不用使用斜杆也可组成几何不变体系，使结构内部具有较大的使用空间，便于使用。刚架的特点：（1）杆件少，内部空间大，便于利用。（2）刚结点处各杆不能发生相对转动，因而各杆件的夹角始终保持不变。（3）刚结点处可以承受和传递弯矩，因而在刚架中弯矩是主要内力。（4）刚架中的各杆通常情况下为直杆，制作加工较方便。根据结构组成特点，静定平面刚架可分为：（1）悬臂刚架：常用于火车站站台（图3-10a）、雨棚等。（2）简支刚架：常用于起重机的刚支架及渡槽横向计算所取的简图等（图3-10b）：（3）三铰刚架：常用于小型厂房、仓库、食堂等结构（图3-10c）。图310a图3-10b图310c刚架结构在土木工程中应用较广。但静定的刚架在工程中应用不多，多为超静定刚架，如房屋建筑结构中的框架结构。解算超静定刚架的内力是建立在静定刚架内力计算基础之上的，所以，必须熟练掌握静定刚架的内力计算方法

教学要求 掌握刚架结构的特点，熟练的求解支座反力和截面内力，熟练绘制刚架结构的内力图。 3.3.1 刚架的特点和分类 刚架：是由若干根直杆（梁和柱）用刚结点（部分可为铰结点）所组成的结构。当组成刚架的 各杆的轴线和外力都在同一平面时，称作平面刚架。 如图3-9a所示为一平面刚架 当B、C处为铰结点时为该结构为几何可变体（图3-9b），要使结构为几何不变体，则需增加斜 杆AC（图3-9c）或把B、C变为刚结点。两种方法相比较，可以看出刚架中由于具有刚结点，因而， 不用使用斜杆也可组成几何不变体系，使结构内部具有较大的使用空间，便于使用。 刚架的特点： （1）杆件少，内部空间大，便于利用。 （2）刚结点处各杆不能发生相对转动，因而各杆件的夹角始终保持不变。 （3）刚结点处可以承受和传递弯矩，因而在刚架中弯矩是主要内力。 （4）刚架中的各杆通常情况下为直杆，制作加工较方便。 根据结构组成特点，静定平面刚架可分为： （1）悬臂刚架：常用于火车站站台（图3-10a）、雨棚等。 （2）简支刚架：常用于起重机的刚支架及渡槽横向计算所取的简图等（图3-10b）； （3）三铰刚架：常用于小型厂房、仓库、食堂等结构（图3-10c）。 刚架结构在土木工程中应用较广。但静定的刚架在工程中应用不多，多为超静定刚架，如房屋 建筑结构中的框架结构。解算超静定刚架的内力是建立在静定刚架内力计算基础之上的，所以，必 须熟练掌握静定刚架的内力计算方法

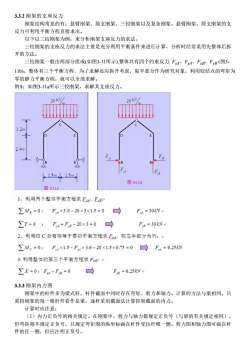
3.3.2刚架的支座反力刚架结构常见的有：悬臂刚架、简支刚架、三铰刚架以及复杂刚架。悬臂刚架、简支刚架的支反力可利用平衡方程直接求出。以下以三铰刚架为例，来分析刚架支座反力的求法。三铰刚架的支座反力的求法主要是充分利用平衡条件来进行计算，分析时经常采用先整体后拆开的方法。三铰刚架一般由两部分组成(如图3-11所示),整体共有四个约束反力：FxA、FyA、FxB、FyB(图311b)。整体有三个平衡方程，为了求解还应拆开考虑，取半部分作为研究对象，利用铰结点的弯矩为零的静力平衡方程，就可以全部求解。例1：如图3-11a所示三铰刚架，求解其支座反力。20kV20kV12#2.4mFBTBA口FLF1.5m1.5m图311b图31131、利用两个整体平衡方程求Fd、F:ZMg=0:Fu×3.0-20×3×1.5=0F=30kVZY=0:FM+Fs-20x3=0DFys=30kV2、利用铰C处弯矩等于零的平衡方程求F，取左半部分为例：ZMc=0:Fx1.5-F×3.6-20×1.5×0.75=0F=6.25RV3.利用整体的第三个平衡方程求FxB:口ZX=0:F4-F=0F=6.25kN3.3.3刚架内力图刚架中的杆件多为梁式杆，杆件截面中同时存在弯矩、剪力和轴力。计算的方法与梁相同。只需将刚架的每一根杆件看作是梁，逐杆采用截面法计算控制截面的内力。计算时应注意：（1）内力正负号的相关规定。在刚架中，剪力与轴力都规定正负号（与梁的有关规定相同），但弯矩则不规定正负号，只规定弯矩图的纵坐标画在杆件受拉纤维一侧。剪力图和轴力图可画在杆件的任一侧，但应注明正负号

3.3.2 刚架的支座反力 刚架结构常见的有：悬臂刚架、简支刚架、三铰刚架以及复杂刚架。悬臂刚架、简支刚架的支 反力可利用平衡方程直接求出。 以下以三铰刚架为例，来分析刚架支座反力的求法。 三铰刚架的支座反力的求法主要是充分利用平衡条件来进行计算，分析时经常采用先整体后拆 开的方法。 三铰刚架一般由两部分组成(如图3-11所示),整体共有四个约束反力: FxA、FyA、FxB、FyB (图3- 11b)。整体有三个平衡方程，为了求解还应拆开考虑，取半部分作为研究对象，利用铰结点的弯矩为 零的静力平衡方程，就可以全部求解。 例1：如图3-11a所示三铰刚架，求解其支座反力。 3.3.3 刚架内力图 刚架中的杆件多为梁式杆，杆件截面中同时存在弯矩、剪力和轴力。计算的方法与梁相同。只 需将刚架的每一根杆件看作是梁，逐杆采用截面法计算控制截面的内力。 计算时应注意： （1）内力正负号的相关规定。在刚架中，剪力与轴力都规定正负号（与梁的有关规定相同）， 但弯矩则不规定正负号，只规定弯矩图的纵坐标画在杆件受拉纤维一侧。剪力图和轴力图可画在杆 件的任一侧，但应注明正负号

（2）结点处有不同的杆端截面。（3）正确选取隔离体。（4）结点处平衡。由于刚架的内力的正负号规定与梁基本相同。为了明确各截面内力，特别是区别相交于同一结点的不同杆端截面的内力，在内力符号右下角采用两个角标，其中第一个角标表示内力所属截面，第二个角标表示该截面所在杆的另一端。例：MAB表示AB杆A端截面的弯矩，MBA则表示AB杆端B截面的弯矩。3.3.4刚架内力图实例分析例2：作出图3-12a所示简支刚架的内力图。20kV20元VD30kV30kV31-RP61图3128图3126解：（1）求支座反力，取整体为隔离体（图3-12b）。ZM,=0:F×6-30×3-20×6×3=0Fs=75kNZY=0:FM=45ANFy+F5-20×6=0Zx=0:F=-30KNF+30=0方法一：（2）作弯矩图，逐杆分段计算控制截面的弯矩，利用作图规律（参见第5页）和叠加法作弯矩图(图3-12c)。BE杆：MsE=0,Ms=0.杆上无荷载，弯矩图为直线。AD杆：MAD=0，MP=-F×4-30×1=90V.m（内侧受拉），C点处作用有集中荷载30kV，该点处，弯矩图有尖角。Mc=Mcp=90KV·m（内侧受拉）DE杆：杆上受均布荷载作用，利用叠加法作弯矩图。杆端弯矩连线叠加简支梁在均布荷载作用下的弯矩图。MDE=90kV·m（内侧受拉），Mep=0kV·m（3）作剪力图

（2）结点处有不同的杆端截面。 （3）正确选取隔离体。 （4）结点处平衡。 由于刚架的内力的正负号规定与梁基本相同。为了明确各截面内力，特别是区别相交于同一结 点的不同杆端截面的内力，在内力符号右下角采用两个角标，其中第一个角标表示内力所属截面， 第二个角标表示该截面所在杆的另一端。 例： MAB表示 AB 杆 A 端截面的弯矩，MBA则表示 AB 杆端 B 截面的弯矩。 3.3.4 刚架内力图实例分析 例2：作出图3-12a所示简支刚架的内力图。 解： （1）求支座反力，取整体为隔离体（图3-12b）。 方法一： （2）作弯矩图，逐杆分段计算控制截面的弯矩，利用作图规律（参见第5页）和叠加法作弯矩 图(图3-12c)。 （3）作剪力图

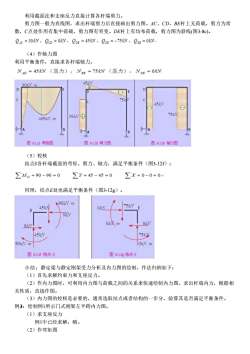
利用截面法和支座反力直接计算各杆端剪力。剪力图一般为直线图，求出杆端剪力后直接画出剪力图。AC、CD、BE杆上无荷载，剪力为常数，C点处作用有集中荷载，剪力图有突变。DE杆上有均布荷载，剪力图为斜线(图3-8c)。QAC=30ANQc=0AV,QD=45KN,QED=-75KN,QEs=0KN（4）作轴力图利用平衡条件，直接求各杆端轴力。ND=45kN（压力），Ns=75kN（压力），NDE=0kV454V90-V.电I75k45kV75130V405kV-mOBLPAYBOO图3120弯矩图图312d剪力图图312e轴力图（5）校核结点D各杆端截面的弯矩、剪力、轴力，满足平衡条件（图3-12f）：ZM,=90-90=0ZY=45-45=0ZX=0-0=00同理，结点E处也满足平衡条件（图3-12g）。90kV-m75kV451OLVORVoe-mORVOV45KV75kyoeV-m90cV-m图312F结点D图312g结点E小结：静定梁与静定刚架受力分析及内力图的绘制，作法归纳如下：（1）首先求解约束力和支座反力。（2）作内力图时，可利用内力图与荷载之间的关系来快速绘制内力图。求出杆端内力，根据相关性质，直接作图。（3）内力图的校核是必要的，通常选取结点或者结构的一步分，验算其是否满足平衡条件。例3：绘制例1所示门式刚架左半跨内力图。（1）求支座反力例1中已经求解，略。（2）作弯矩图

利用截面法和支座反力直接计算各杆端剪力。 剪力图一般为直线图，求出杆端剪力后直接画出剪力图。AC、CD、BE杆上无荷载，剪力为常 数，C点处作用有集中荷载，剪力图有突变。DE杆上有均布荷载，剪力图为斜线(图3-8c)。 （4）作轴力图 利用平衡条件，直接求各杆端轴力。 （5）校核 结点D各杆端截面的弯矩、剪力、轴力，满足平衡条件（图3-12f）： 同理，结点E处也满足平衡条件（图3-12g）。 小结：静定梁与静定刚架受力分析及内力图的绘制，作法归纳如下： （1）首先求解约束力和支座反力。 （2）作内力图时，可利用内力图与荷载之间的关系来快速绘制内力图。求出杆端内力，根据相 关性质，直接作图。 （3）内力图的校核是必要的，通常选取结点或者结构的一步分，验算其是否满足平衡条件。 例3：绘制例1所示门式刚架左半跨内力图。 （1）求支座反力 例1中已经求解，略。 （2）作弯矩图

首先求解杆端弯矩：Mp=15KV·m（外侧受拉）杆DC中点弯矩为：15-1x×20×1.5*=1.875kNV-m（外侧受拉）。方法一：281方法二：30×0.75-6.25×3-×20×0.75=1.875（外侧受拉）2方法一：利用叠加原理，杆端弯矩图叠加相应简支梁在均布荷载作用下的弯矩图。方法二：直接以左半边为隔离体，利用平衡条件求解。两种方法结果相同，在结构承受荷载较为简单时，方法一比较简单；承受荷载情况比较复杂时，以第二种方法较为简单。（3）作剪力图杆端剪力同样可以采取上述两种方法来求解。AD杆：选取截面一边AD为隔离体，利用平衡条件求解。FoDA=FQ4D=-6.25kVDC杆：选取DC为隔离体，受力图见图3-13a。1x(1.875+20x1.5x.0.75)=12.7kVFo1.921x(1.875-20×1.5x0.75)=10.74kVFocD1.9220元01.875l.V-mODFD图3138（4）作轴力图AD杆：选取截面一边AD为隔离体，利用平衡条件求解。FNAD=FNDA=-30KNDC杆：可选取结点D为隔离体，由于轴力的方向是杆件轴线方向，所以，在建立平衡方程时，方便起见沿DC的轴线列投影方程：sinα=0.625cosq=0.781Fypc=6.25xcosα+30xsinα=23.63kN（5）作内力图根据内力与荷载之间的关系，由杆端内力直接作内力图

方法一：利用叠加原理，杆端弯矩图叠加相应简支梁在均布荷载作用下的弯矩图。 方法二：直接以左半边为隔离体，利用平衡条件求解。 两种方法结果相同，在结构承受荷载较为简单时，方法一比较简单；承受荷载情况比较复杂 时，以第二种方法较为简单。 （3）作剪力图 杆端剪力同样可以采取上述两种方法来求解。 AD杆：选取截面一边AD为隔离体，利用平衡条件求解。 （4）作轴力图 AD杆：选取截面一边AD为隔离体，利用平衡条件求解。 （5）作内力图 根据内力与荷载之间的关系，由杆端内力直接作内力图