《结构力学》课程授课教案（讲义）第三章 静定结构的受力分析 3.6 三铰拱

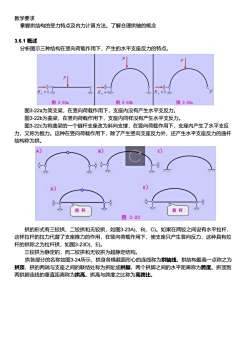
教学要求掌握拱结构的受力特点及内力计算方法。了解合理拱轴的概念3.6.1概述分析图示三种结构在竖向荷载作用下，产生的水平支座反力的特点H.H.H图3-22a图3-22b图3-22c图3-22a为简支梁，在竖向荷载作用下，支座内没有产生水平支反力。图3-22b为曲梁，在竖向荷载作用下，支座内同样没有产生水平支反力。图3-22c为将曲梁的一个链杆支座改为斜向支撑，在竖向荷载作用下，支座内产生了水平支反力，又称为推力。这种在竖向荷载作用下，除了产生竖向支座反力外，还产生水平支座反力的曲杆结构称为拱。A)BE)DS拉杆拉杆图3-23拱的形式有三铰拱、二铰拱和无铰拱，如图3-23A、B)、C)。如果在两铰之间设有水平拉杆这样拉杆的拉力代替了支座推力的作用，在竖向荷载作用下，使支座只产生竖向反力，这种具有拉杆的拱称之为拉杆拱，如图3-23D)、E)。三铰拱为静定的，而二铰拱和无铰拱为超静定结构拱各部分的名称如图3-24所示，拱身各横截面形心的连线称为拱轴线。拱结构最高一点称之为拱顶，拱的两端与支座之间的联结处称为拱趾或拱脚。两个拱脚之间的水平距离称为跨度。拱顶到两拱脚连线的垂直距离称为拱高。拱高与跨度之比称为高跨比

教学要求 掌握拱结构的受力特点及内力计算方法。了解合理拱轴的概念 3.6.1 概述 分析图示三种结构在竖向荷载作用下，产生的水平支座反力的特点。 图3-22a为简支梁，在竖向荷载作用下，支座内没有产生水平支反力。 图3-22b为曲梁，在竖向荷载作用下，支座内同样没有产生水平支反力。 图3-22c为将曲梁的一个链杆支座改为斜向支撑，在竖向荷载作用下，支座内产生了水平支反 力，又称为推力。这种在竖向荷载作用下，除了产生竖向支座反力外，还产生水平支座反力的曲杆 结构称为拱。 拱的形式有三铰拱、二铰拱和无铰拱，如图3-23A)、B)、C)。如果在两铰之间设有水平拉杆， 这样拉杆的拉力代替了支座推力的作用，在竖向荷载作用下，使支座只产生竖向反力，这种具有拉 杆的拱称之为拉杆拱，如图3-23D)、E)。 三铰拱为静定的，而二铰拱和无铰拱为超静定结构。 拱各部分的名称如图3-24所示，拱身各横截面形心的连线称为拱轴线。拱结构最高一点称之为 拱顶，拱的两端与支座之间的联结处称为拱趾或拱脚。两个拱脚之间的水平距离称为跨度。拱顶到 两拱脚连线的垂直距离称为拱高。拱高与跨度之比称为高跨比

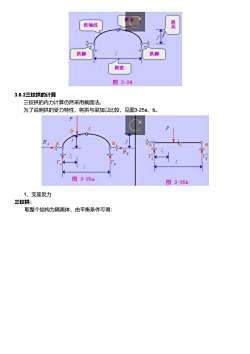
面拱高拱轴线拱脚拱脚跨度图3-243.6.2三铰拱的计算三铰拱的内力计算仍然采用截面法为了说明拱的受力特性，将拱与梁加以比较，见图3-25a、b。PCDHH图3-25a图3-25b1、支座反力三铰拱：取整个结构为隔离体，由平衡条件可得：

3.6.2三铰拱的计算 三铰拱的内力计算仍然采用截面法。 为了说明拱的受力特性，将拱与梁加以比较，见图3-25a、b。 1、支座反力 三铰拱： 取整个结构为隔离体，由平衡条件可得：

2M-0=V,-P4ZM,-0=V=P(-)取右半边为隔离体：ZM,=0=H,xJ=V,xI=H,-P421由整体：ZX-0=H,-H,-PA21简支梁：ZM,-0=V-PLZM,-0=V-p(-4)比较可得：三铰拱与简支梁的竖向支反力完全相同.注意到水平支反力式中的分子就是简支梁上截面C的弯矩M=P么，，则水平支反力可写作：M:=H+H-H=由上式可知，在竖向荷载作用下，水平支反力的大小与拱轴形式即拱轴线形状无关，而只决定于A、B、C三铰的位置。若竖向荷载和拱脚位置给定不变，则随着拱高的增大，水平推力减小。反之，拱高变小，水平推力增大。若当0时，推力为无穷大，这时A、B、C三铰在一直线上，成为几何可变体系。2、内力的计算公式在求得支座反力后，即可求解出拱轴上任一截面上的三种内力：弯矩、剪力、轴力。现以拱轴上任意截面K为例(图3-26a)，导出其内力计算公式：CEOrH图3-26a从图3-26a中取截取K截面以左半部分为隔离体。K截面上的内力分别以Mk、Qk、Nk来表示，K截面的位置可由其形心位置xk、yk和该处拱轴切线的倾角Pk确定

由上式可知，在竖向荷载作用下，水平支反力的大小与拱轴形式即拱轴线形状无关，而只决定于 A、B、C三铰的位置。若竖向荷载和拱脚位置给定不变，则随着拱高f的增大，水平推力减小。反 之，拱高变小，水平推力增大。若当f=0时，推力为无穷大，这时A、B、C三铰在一直线上，成为几 何可变体系。 2、内力的计算公式 在求得支座反力后，即可求解出拱轴上任一截面上的三种内力：弯矩、剪力、轴力。现以拱轴上 任意截面K为例(图3-26a)，导出其内力计算公式： 从图3-26a中取截取K截面以左半部分为隔离体。K截面上的内力分别以MK、QK、NK来表示， K截面的位置可由其形心位置xK、yK和该处拱轴切线的倾角φK确定

（1）弯矩的计算公式由隔离体平衡条件可得：Mx=Vaax-Hyxt由于V=V，故上式可改写为：Mx=M-Hyxt即拱内任一截面上的弯矩等于相应简支梁上对应的截面上的弯矩减去推力所引起的弯矩HyK。由此可见由于推力的存在，拱的弯矩比相应梁的弯矩要小。（2）剪力的计算公式将截面K上所有的内力沿截面K上投影，可得：Ox=V,cosOx-Hsinox=Qcosox-HsinxC(3）轴力的计算公式将截面K上所有内力没截面K得法线方向进行投影求代数和，可得：+Nx=VsinPx+Hcosx=OsinOx+HcosOx综上所述，三铰拱在坚向荷载作用下，任一截载面上的弯矩、剪力荷轴力的计算公式如下：*M=M-HyxQx=QcosOx-HsinOxNx=Qu sin Ox+Hcosox3.6.3合理拱轴的概念拱在竖向荷载作用下，各截面上一般产生三个内力，即弯矩、剪力、轴力。截面处于偏心受压状态，其正应力分布不均匀。但是通过合理选取一根适当的拱轴线，使得在给定的荷载作用下，拱上各截面的弯矩均为零，即只承受轴力。此时，各截面都处于均匀受压状态，因而材料的性能得到充分的利用，相应的拱截面尺寸是最小的。从理论上来讲，设计成这样的拱是最经济的，故称这样的拱轴为合理拱轴。任一截面上的弯矩为：CMg=M-Hye利用截面上的弯矩为零的条件，可找出合理拱轴。由上式可知，在荷载和跨度给定的情况下，M&即可确定，而推力H-，当拱跨基拱高一经确定，H也为J给定值。所以要使弯矩等于零，只要调整拱轴上各点的纵标。写成一般式：MM-M°-Hy=0三H

（1）弯矩的计算公式 由隔离体平衡条件可得： 即拱内任一截面上的弯矩等于相应简支梁上对应的截面上的弯矩减去推力所引起的弯矩HyK。由 此可见由于推力的存在，拱的弯矩比相应梁的弯矩要小。 （2）剪力的计算公式 将截面K上所有的内力沿截面K上投影，可得： 3.6.3 合理拱轴的概念 拱在竖向荷载作用下，各截面上一般产生三个内力，即弯矩、剪力、轴力。截面处于偏心受压状 态，其正应力分布不均匀。但是通过合理选取一根适当的拱轴线，使得在给定的荷载作用下，拱上 各截面的弯矩均为零，即只承受轴力。此时，各截面都处于均匀受压状态，因而材料的性能得到充 分的利用，相应的拱截面尺寸是最小的。从理论上来讲，设计成这样的拱是最经济的，故称这样的 拱轴为合理拱轴。 任一截面上的弯矩为：

合理拱轴的竖标与相应简支梁的弯矩成正比。当拱上所受荷载为已知时，只要求出相应简支梁的弯矩方程，然后除以H，即得三铰拱的合理拱轴的轴线方程

合理拱轴的竖标与相应简支梁的弯矩成正比。当拱上所受荷载为已知时，只要求出相应简支梁 的弯矩方程，然后除以H，即得三铰拱的合理拱轴的轴线方程