《结构力学》课程授课教案（讲义）第三章 静定结构的受力分析 3.1 梁的内力计算回顾

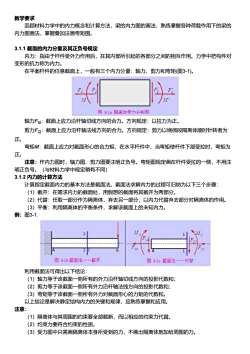
教学要求回顾材料力学中的内力概念和计算方法，梁的内力图的画法，熟练掌握各种荷载作用下的梁的内力图画法，掌握叠加法画弯矩图。3.1.1截面的内力分量及其正负号规定内力：指由于杆件受外力作用后，在其内部所引起的各部分之间的相互作用。力学中把构件对变形的抗力称为内力。在平面杆件的任意截面上，一般有三个内力分量：轴力、剪力和弯矩（图3-1)。EExEM图31a隔离体受力分析图轴力F：截面上应力沿杆轴切线方向的合力。方向规定：以拉力为正。剪力FQ：截面上应力沿杆轴法线方向的合力。方向规定：剪力以绕微段隔离体顺时针转者为正。弯矩M：截面上应力对截面形心的合力矩，在水平杆件中，当弯矩使杆件下部受拉时，弯矩为正。注意：作内力图时，轴力图、剪力图要注明正负号。弯矩图规定画在杆件受拉的一侧，不用注明正负号。（与材料力学中规定稍有不同）3.1.2内力的计算方法计算指定截面内力的基本方法是截面法。截面法求解内力的过程可归纳为以下三个步骤：（1）截开：在需求内力的截面处，用假想的截面将其截开为两部分。（2）代替：任取一部分作为隔离体，弃去另一部分，以内力代替弃去部分对隔离体的作用。（3）平衡：利用隔离体的平衡条件，求解该截面上的未知内力。例：图3-1.M1图31b截面法一一截开图31c截面法一一代替利用截面法可得出以下结论：（1）轴力等于该截面一侧所有的外力沿杆轴切线方向的投影代数和；（2）剪力等于该截面一侧所有外力沿杆轴法线方向的投影代数和（3）弯矩等于该截面一侧所有外力对截面形心的力矩的代数和。以上结论是解决静定结构内力的关键和规律，应熟练掌握和应用。注意：（1）隔离体与其周围的约束要全部截断，而以相应的约束力代替。（2）约束力要符合约束的性质。（3）受力图中只需画隔离体本身所受到的力，不画出隔离体施加给周围的力

教学要求 回顾材料力学中的内力概念和计算方法，梁的内力图的画法，熟练掌握各种荷载作用下的梁的 内力图画法，掌握叠加法画弯矩图。 3.1.1 截面的内力分量及其正负号规定 内力：指由于杆件受外力作用后，在其内部所引起的各部分之间的相互作用。力学中把构件对 变形的抗力称为内力。 在平面杆件的任意截面上，一般有三个内力分量：轴力、剪力和弯矩(图3-1)。 轴力FN：截面上应力沿杆轴切线方向的合力。方向规定：以拉力为正。 剪力FQ：截面上应力沿杆轴法线方向的合力。方向规定：剪力以绕微段隔离体顺时针转者为 正。 弯矩M：截面上应力对截面形心的合力矩，在水平杆件中，当弯矩使杆件下部受拉时，弯矩为 正。 注意：作内力图时，轴力图、剪力图要注明正负号。弯矩图规定画在杆件受拉的一侧，不用注 明正负号。（与材料力学中规定稍有不同） 3.1.2 内力的计算方法 计算指定截面内力的基本方法是截面法。截面法求解内力的过程可归纳为以下三个步骤： （1）截开：在需求内力的截面处，用假想的截面将其截开为两部分。 （2）代替：任取一部分作为隔离体，弃去另一部分，以内力代替弃去部分对隔离体的作用。 （3）平衡：利用隔离体的平衡条件，求解该截面上的未知内力。 例：图3-1. 利用截面法可得出以下结论： （1）轴力等于该截面一侧所有的外力沿杆轴切线方向的投影代数和； （2）剪力等于该截面一侧所有外力沿杆轴法线方向的投影代数和； （3）弯矩等于该截面一侧所有外力对截面形心的力矩的代数和。 以上结论是解决静定结构内力的关键和规律，应熟练掌握和应用。 注意： （1）隔离体与其周围的约束要全部截断，而以相应的约束力代替。 （2）约束力要符合约束的性质。 （3）受力图中只需画隔离体本身所受到的力，不画出隔离体施加给周围的力

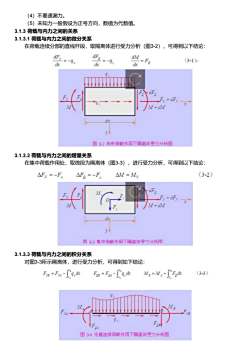
（4）不要遗漏力。（5）未知力一般假设为正号方向，数值为代数值。3.1.3荷载与内力之间的关系3.1.3.1荷载与内力之间的微分关系在荷载连续分部的直线杆段，取隔离体进行受力分析（图3-2），可得到以下结论：dFg=dFy=-4xdM=Fo(3-1)=-9,dxdxdrOtdFFFy+dFyMM+aM图32均布荷载作用下隔离体受力分析图3.1.3.2荷载与内力之间的增量关系在集中荷载作用处，取微段为隔离体（图3-3），进行受力分析，可得到以下结论：(3-2)AFy=-FxAF=-F,AM=M-aF.山MAFF+dFM+dx1图33集中石载作用下隔离体受力分析图3.1.3.3荷载与内力之间的积分关系对图3-3所示隔离体，进行受力分析，可得到如下结论(3-3)Fxs=Fx-'qdxM,=M.+'FodrFos=Fou-',dx11BFEE9xC.图34任意连续荷载作用下隔离体受力分析图

（4）不要遗漏力。 （5）未知力一般假设为正号方向，数值为代数值。 3.1.3 荷载与内力之间的关系 3.1.3.1 荷载与内力之间的微分关系 在荷载连续分部的直线杆段，取隔离体进行受力分析（图3-2），可得到以下结论： 3.1.3.2 荷载与内力之间的增量关系 在集中荷载作用处，取微段为隔离体（图3-3），进行受力分析，可得到以下结论： 3.1.3.3 荷载与内力之间的积分关系 对图3-3所示隔离体，进行受力分析，可得到如下结论：

根据内力与荷载之间的关系，可归纳下面几条规律（1）无分布荷载区段，弯矩图为直线，剪力图为平行于轴线的直线（2）有均布荷载区段，弯矩图为曲线，曲线的图像与均布荷载的指向一致，剪力图为一斜直线。（3）集中力作用处，剪力图有突变，突变值大小等于该集中力的数值。弯矩图的斜率也发生变化，弯矩图上有尖角。（4）集中力偶作用处，剪力图无变化，弯矩图发生突变，突变数值等于集中力偶的数值。3.1.4分段叠加法作弯矩图3.1.4.1叠加原理应用叠加原理可以使结构的计算简化，虽然对于实际结构而言，叠加原理是近似的，但只要满足以下条件，所得的结果是足够精确的。（1）几何线性条件当结构的变形与结构本身的尺寸相比极为微小时，称为小变形结构。在小变形结构计算中，变形所带来的荷载位置变化及杆件尺寸变化的影响可以忽略不计，因而，允许用变形前的尺寸来进行计算，这就满足了叠加的几何条件。（2）物理线性条件结构材料的受力与变形的物理关系为线性弹性关系，即服从虎克定律。则在物理上提供了线性叠加条件。满足以上条件的结构，才可以应用叠加原理：在小变形和材料符合虎克定律的前提下，结构在几个荷载共同作用下产生的内力等于各个荷载单独作用产生的内力的代数合。能够应用叠加原理的结构称之为线性结构。利用叠加原理做弯矩图，即先分别作出各个单独荷载作用时的弯矩图，然后将其相应的纵坐标叠加。（如图3-5演示过程）：C-一g2川Bai十图35叠加原理作弯矩图

根据内力与荷载之间的关系，可归纳下面几条规律： （1）无分布荷载区段，弯矩图为直线，剪力图为平行于轴线的直线 （2）有均布荷载区段，弯矩图为曲线，曲线的图像与均布荷载的指向一致，剪力图为一斜直 线。 （3）集中力作用处，剪力图有突变，突变值大小等于该集中力的数值。弯矩图的斜率也发生变 化，弯矩图上有尖角。 （4）集中力偶作用处，剪力图无变化，弯矩图发生突变，突变数值等于集中力偶的数值。 3.1.4 分段叠加法作弯矩图 3.1.4.1 叠加原理 应用叠加原理可以使结构的计算简化，虽然对于实际结构而言，叠加原理是近似的，但只要满 足以下条件，所得的结果是足够精确的。 （1）几何线性条件 当结构的变形与结构本身的尺寸相比极为微小时，称为小变形结构。在小变形结构计算中，变 形所带来的荷载位置变化及杆件尺寸变化的影响可以忽略不计，因而，允许用变形前的尺寸来进行 计算，这就满足了叠加的几何条件。 （2）物理线性条件 结构材料的受力与变形的物理关系为线性弹性关系，即服从虎克定律。则在物理上提供了线性 叠加条件。 满足以上条件的结构，才可以应用叠加原理： 在小变形和材料符合虎克定律的前提下，结构在几个荷载共同作用下产生的内力等于各个荷载 单独作用产生的内力的代数合。 能够应用叠加原理的结构称之为线性结构。 利用叠加原理做弯矩图,即先分别作出各个单独荷载作用时的弯矩图，然后将其相应的纵坐标叠 加。（如图3-5演示过程）:

3.1.4.2分段叠加原理上述叠加法同样可用于绘制结构中任意直杆段的弯矩图。如图3-6演示过程C7-1福FEFB图36分段叠加法作弯矩图（1）选定外力不连续点作为控制截面（如集中荷载作用点、集中力偶作用点、分布荷载的起点和终点等），求出控制截面的弯矩值。（2）分段画弯矩图，当控制截面间无荷载作用时，根据控制截面的弯矩值，即可作出直线弯矩图；当有荷载作用时，还需叠加这一段按简支梁求得的弯矩图。利用分段叠加法求弯矩可用如下公式：M=M+MAB段中点的弯矩值：M-M.+Ms2注意：在利用叠加原理作弯矩图时，弯矩图的叠加是指两个弯矩图纵坐标的叠加，而不是两个弯矩图图形简单的拼合

3.1.4.2 分段叠加原理 上述叠加法同样可用于绘制结构中任意直杆段的弯矩图。如图3-6演示过程。 （1）选定外力不连续点作为控制截面（如集中荷载作用点、集中力偶作用点、分布荷载的起点 和终点等），求出控制截面的弯矩值。 （2）分段画弯矩图，当控制截面间无荷载作用时，根据控制截面的弯矩值，即可作出直线弯矩 图；当有荷载作用时，还需叠加这一段按简支梁求得的弯矩图。 注意：在利用叠加原理作弯矩图时，弯矩图的叠加是指两个弯矩图纵坐标的叠加，而不是两个 弯矩图图形简单的拼合