《结构力学》课程教学资源（课件讲稿）第三章 静定结构的受力分析（刚架-组合结构）

2013-6-253-3静定平面刚架教学要求：了解刚架的特点。■掌握刚架的支座反力和截面内力的计算。■掌握刚架内力图的绘制。主要内容：■刚架的特点■刚架的内力计算和内力图3-3静定平面刚架3-3静定平面刚架1.刚架的特点（2）静定平面刚架的分类（1）平面刚架的定义起重机的刚支架小型厂房、仓库火车站站台刚架：由若干根直杆（梁和柱）用刚结点（部分可为铰结点）所组成的结构。平面刚架：组成刚架的各杆的轴线和外力在同一平面。&刚结点铰结点力TT770悬臂刚架简支刚架三铰刚架3-3静定平面刚架3-3静定平面刚架（3）刚架的特点：2.刚架的内力计算》内部空间大，便于利用。内力类型弯矩、剪力、轴力刚结点处各杆不能发生相对转动，因而各计算方法：截面法杆件的夹角始终保持不变。内力的符号规定：刚结点处可以承受和传递弯矩。弯矩：弯矩图画在受拉一侧。ACT009----.剪力：使杆段顺时针转动为正。90°90°Z9轴力：拉力为正

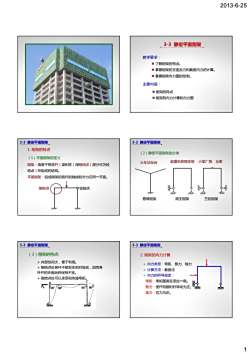
2013-6-25 1 教学要求： „ 了解刚架的特点。 „ 掌握刚架的支座反力和截面内力的计算。 3-3 静定平面刚架 „ 掌握刚架内力图的绘制。 主要内容： „ 刚架的特点 „ 刚架的内力计算和内力图 1. 刚架的特点 （1）平面刚架的定义 刚架：由若干根直杆（梁和柱）用刚结点（部分可为铰 结点）所组成的结构。 平面刚架：组成刚架的各杆的轴线和外力在同一平面 3-3 静定平面刚架 。 刚结点 铰结点 （2）静定平面刚架的分类 火车站站台 起重机的刚支架 小型厂房、仓库 3-3 静定平面刚架 悬臂刚架 简支刚架 三铰刚架 ¾ 内部空间大，便于利用。 ¾ 刚结点处各杆不能发生相对转动，因而各 杆件的夹角始终保持不变。 ¾ 刚结点处可以承受和传递弯矩。 （3）刚架的特点: 3-3 静定平面刚架 ™ 内力类型：弯矩、剪力、轴力 ™ 计算方法：截面法 ™ 内力的符号规定： 弯矩 弯矩 在 拉 侧 2. 刚架的内力计算 3-3 静定平面刚架 ：弯矩图画在受拉一侧。 剪力：使杆段顺时针转动为正。 轴力：拉力为正

2013-6-253-3静定平面刚架示例3-3静定平面刚架示例例2：例1：10kN/m计算步骤：量星TBVC（1）计算支座反力NO（2）求杆端内力AA（3）作内力图（4）结点校核MM2m1m3-3静定平面刚架3-3静定平面刚架示例小结例3：20kN/m刚架特点刚结点处各杆件的夹角始终保持不变，D主要内力是弯矩C》刚架内力图绘制的解题步骤HANA求支座反力，杆端内力，作内力图。V7ImC3-4静定平面刚架3-4静定平面桁架教学要求：■了解静定平面行架的受力特点。■掌握静定平面架内力计算的方法：L90X:3X2.450=7350一结点法、载面法5000主要内容：钢筋混凝土组合屋架■桁架的特点和组成■桁架内力计算方法2

2013-6-25 2 （1）计算支座反力 计算步骤： （2）求杆端内力 m 10kN/m 示例 B 例1： 3-3 静定平面刚架 1m （4）结点校核 （3）作内力图 2m A VA HA MA B C 10kN/m m 例2： VC 3-3 静定平面刚架 示例 A 2m 1 2 VA HA 1m C 20kN/m D E 例3： 3-3 静定平面刚架 示例 1m 1 A B 1m VA HA VB HB ¾ 刚架特点 刚结点处各杆件的夹角始终保持不变， 主要内力是弯矩； 3-3 静定平面刚架 小结 ¾ 刚架内力图绘制的解题步骤 求支座反力，杆端内力，作内力图。 教学要求： 3-4 静定平面桁架 „ 了解静定平面桁架的受力特点。 „ 掌握静定平面桁架内力计算的方法： „ 桁架的特点和组成 „ 桁架内力计算方法 主要内容： ——结点法、截面法 3-4 静定平面刚架 钢筋混凝土组合屋架

2013-6-253-4静定平面刚架3-4静定平面刚架.128m#武汉长江大桥采用的架形式3-4静定平面刚架3-4静定平面刚架1.桁架的特点和组成桁架的各部分名称定义：结点均为铰结点的结构。上弦杆腹杆群杆的内力主要是轴力。H》内力计算中的基本假定桁架的结点为光滑的铰结点。下弦杆各杆的轴线均为直线且通过铰心。节间长度d荷载和支座反力都作用在结点上。跨度L3-4静定平面刚架分类3-4静定平面刚架分类》按几何组成分》按不同特征分简单桁架：平行弦桁架折弦桁梁由基本铰结三角形或基础，NN依次增加二元体组成。联合行架：由几个简单桁架联合组成的梯形桁架三角形桁架几何不变的铰结体系。AAAN复杂行架：非前两种为复杂行架3

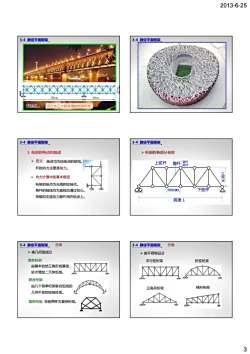
2013-6-25 3 3-4 静定平面刚架 武汉长江大桥采用的桁架形式 3-4 静定平面刚架 1. 桁架的特点和组成 ¾ 定义: 结点均为铰结点的结构。 ¾ 内力计算中的基本假定 杆的内力主要是轴力。 3-4 静定平面刚架 桁架的结点为光滑的铰结点。 各杆的轴线均为直线且通过铰心。 荷载和支座反力都作用在结点上。 ¾ 内力计算中的基本假定 ¾ 桁架的各部分名称 上弦杆 腹杆 斜杆 竖杆 3-4 静定平面刚架 跨度 L 节间长度d 下弦杆 简单桁架: 联合桁架: 分类 ¾ 按几何组成分 由基本铰结三角形或基础， 依次增加二元体组成。 3-4 静定平面刚架 联合桁架: 复杂桁架: 非前两种为复杂桁架。 由几个简单桁架联合组成的 几何不变的铰结体系。 ¾ 按不同特征分 平行弦桁架 折弦桁梁 3-4 静定平面刚架 分类 三角形桁架 梯形桁架

2013-6-253-4静定平面刚架2桁架内力的计算方法3-4静定平面刚架2.架内力的计算方法例：求杆FC的内力。例：求杆FC的内力。usOGOGIO+15KNII￥15kN15kN+15kN+15kN+15kN4m4m/4m4m4m4m1分析：分析：结点法+NFE结点GNEDKNGE隔离体：F截面法NeCOG结点FNGF截一代一平PGNFGNENEC15kNT1515kN15kN3-4静定平面刚架3-4静定平面刚架3.零杆usN,=0OGN,NO+15kN+15kN+15kN4m4mL4mJN=0(N,=0隔离体：结点D零杆内力为零的杆T形结点L形结点DNDENDBNpC=03-4静定平面刚架3.零杆3-4静定平面刚架载面单杆零杆的判断任意隔离体中，除某一杆件外，其它所有待求内力的杆件均相交一点时，则此杆件为该截面的截面单杆。AANVLA截面单杆的内力可直接根据隔离体平衡条件求出4

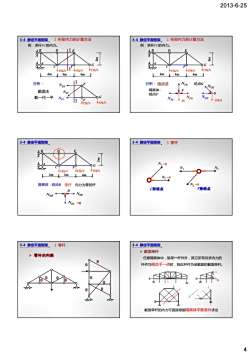
2013-6-25 4 15kN 15kN 15kN A B G C D E F 2. 桁架内力的计算方法 4m 4m 4m 3m 例：求杆FC的内力。 Ⅰ Ⅰ 3-4 静定平面刚架 4m 4m 4m 分析： 截面法 截—代—平 NED NEC NFC G E F 15kN 15kN Ⅰ Ⅰ 15kN 15kN 15kN A B G C D E F 2. 桁架内力的计算方法 4m 4m 4m 3m 例：求杆FC的内力。 3-4 静定平面刚架 4m 4m 4m 分析： 结点法 NFC NFE 隔离体： F 结点F 15 NFG NGF NGE G 15kN 结点G 15kN 15kN 15kN A B G C D E F 4m 4m 4m 3m 3-4 静定平面刚架 NDB NDC D 隔离体：结点D NDE 零杆 内力为零的杆 =0 N1 N N1 N2 =0 0 3-4 静定平面刚架 3. 零杆 N2 L形结点 N3 T形结点 =0 =0 ¾ 零杆的判断 0 0 0 0 0 0 0 3-4 静定平面刚架 3. 零杆 0 0 0 0 0 ¾ 截面单杆 任意隔离体中，除某一杆件外，其它所有待求内力的 杆件均相交于一点时，则此杆件为该截面的截面单杆。 O 3-4 静定平面刚架 y 截面单杆的内力可直接根据隔离体平衡条件求出

2013-6-253-4静定平面刚架示例3-4梁静定平面刚架：示例1.求图示平面行架结构中指定杆件a~d的内力。1.求图示平面桁架结构中指定杆件a~d的内力。NNZZ3MAWAL314TpHN+PZ72V=1.5PV.=1.5PV,=1.5PR=1.5F6d6d(2)求内力NN.解：（1）求支座反力（2）求内力N.N,N1.5P3-4静定平面刚架示例3-4静定平面刚架示例>求图示桁架指定杆件内力（只需指出所选截面）Z区对称性正对称性反对称性3-5组合结构3-5组合结构结构特点一桁架和梁1桥梁钢筋混凝土m797797角钢一-加固工程屋架5

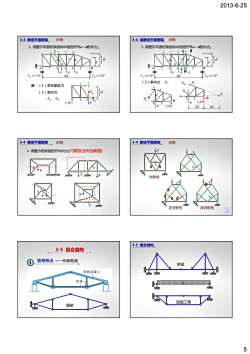
2013-6-25 5 示例 1. 求图示平面桁架结构中指定杆件a～d的内力。 A B 12345 1’ 2’ 3’ 4’ d d 3 4 P P P a b c d 3-4 静定平面刚架 Ι Ι 6d 解：（1）求支座反力 （2）求内力 2’ d 3 4 1’ 1 2 1.5P P Na Nb Na Nb VA =1.5P VB =1.5P 示例 1. 求图示平面桁架结构中指定杆件a～d的内力。 A B 12345 1’ 2’ 3’ 4’ d d 3 4 P P P a b c d 3-4 梁静定平面刚架 ΙΙ ΙΙ ΙΙΙ ΙΙΙ VA =1.5P 6d VB =1.5P Nc B 4 5 4’ P 1.5P d e （2）求内力 Nd k 2d Nd 4 5 B P 1.5P 2d Nc N ¾ 求图示桁架指定杆件内力(只需指出所选截面) P b P P b 3-4 静定平面刚架 示例 P a P b P b 0 0 对称性 示例 b a 3-4 静定平面刚架 正对称性 反对称性 b a b a 0 0 0 0 0 13 ——桁架和梁 3-5 组合结构 屋架 桥梁 3-5 组合结构 加固工程

2013-6-253-5组合结构3-5组合结构高层建筑内力计算截面法2》区分桁架杆件和受弯杆件。选取脱离体时不要切断受弯杆件。先计算架杆件，后计算受弯杆件。3-5组合结构示例3-5组合结构例：绘制内力图讨论：M.大小29o3-6三铰拱3-6三拱应用>杆轴线为曲线；桥梁，也适用于宽的大厅，如礼堂、展览馆、体育馆和商场等。》在竖向荷载作用下产生水平反力。6

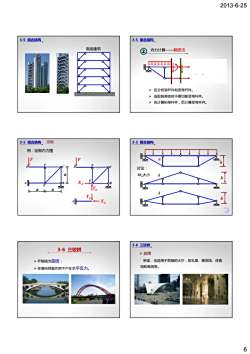
2013-6-25 6 3-5 组合结构 高层建筑 23 3-5 组合结构 内力计算——截面法 ¾ 区分桁架杆件和受弯杆件。 ¾ 选取脱离体时不要切断受弯杆件。 ¾ 先计算桁架杆件，后计算受弯杆件。 例：绘制内力图 D C F a F D C F F 3-5 组合结构 示例 A B E a a B E XE YE A XE YE 讨论： h h A MA大小 A 3-5 组合结构 h h A ¾ 杆轴线为曲线； ¾ 在竖向荷载作用下产生水平反力。 3-6 三铰拱 ¾ 应用 桥梁，也适用于宽敞的大厅，如礼堂、展览馆、体育 馆和商场等。 3-6 三铰拱

2013-6-253-6三铰拱3-6三铰拱类型1.内力计算内力类型M、Q、N三铰拱两铰拱无铰拱拉杆拱内侧受拉为正！轴力压为正顺时针转动为正》拱的各部分名称拱顶拱轴线多》计算方法拱高f趾趾工高跨比be89截面法起拱线L跨度L3-6三铰拱3-6三铰拱(1)支座反力（2)内力的计算6a=VoV=F.AQk=Q%cosPk-HsinPkmoaID!V=F=VOANx=Q sinPx+H cosPkERHBMHM= M- HykH=HRV0.51051f0.50.5BVo=EbV=F,"FQ%=Vo-FpPEP11么F1797M =Vixx-Fp(xx -a)voM°=0.5VoVBVQ=Qcos@-Hsin@3-6三铰拱、示例3-6三拱、示例N=g'sin@+Hcos?-%x(-)例：三铰拱的轴线为抛物线：V=（2）内力的计算截面D的几何参数：M=M°-Hy试求支座反力，D截面的内力，并绘制内力图。y,=3m sin@,=-0.447cos@,=0.894IkN/mIkN/mQD=-5KN4kN4kN(1)支座反力ytQ左=-1kNPH4m5.4mHV, =V -7KN(1)64Vn.IM,=2kN-m5x11219797V.=V-5KN(0)M,=2kN-m4m4m4m/4m8m8mMC=6kN5 Q =1.79kNQ = -1.79kNH4f.N=5.81kNN=7.61kNx(1-x)7

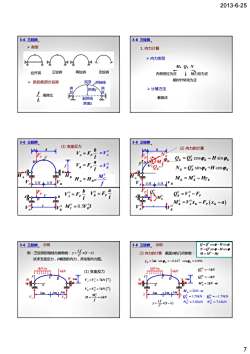
2013-6-25 7 ¾ 类型 拉杆拱 三铰拱 两铰拱 无铰拱 3-6 三铰拱 ¾ 拱的各部分名称 跨度L 起拱线 拱顶 拱 拱高ƒ 趾 拱 趾 拱轴线 高跨比 L f 1. 内力计算 ¾ 内力类型 M、Q、N 内侧受拉为正 轴力压为正 3-6 三铰拱 ¾ 计算方法 截面法 轴力压为正 顺时针转动为正 内侧受拉为正 f A B C a b D FP HA HB A P b V F l = B P a V F l = 0.5V l B 0 =VA 0 =VB 0 M (1) 支座反力 3-6 三铰拱 0.5l 0.5l l A B D FP VA VB A B 0.5 B A B V l H H f = = 0 A P b V F l = 0 B P a V F l = 0 VA 0 VB C 0 0 0.5 M Vl C B = MC f = x H f A B C a b D FP y K x( K , yK ) H QK MK NK ϕ K 0 = − cos sin QQ H KK K K ϕ ϕ 0 = sin + cos NQ H KK K K ϕ ϕ 0 MMH (2) 内力的计算 3-6 三铰拱 VB HB 0.5l 0.5l l A D B FP K 0 QK 0 MK 0 0 QVF KAP = − ( ) 0 0 M Vx F x a K AK P K =− − VA HA 0 VA 0 VB 0 MMH KK K = − y ( ) 2 4 f y xl x l 例：三铰拱的轴线为抛物线： = − 试求支座反力，D截面的内力，并绘制内力图。 4m C D 1 /m kN 4kN y ( ) 0 H H V V kN 7 ↑ 3-6 三铰拱 示例 (1) 支座反力 4m 8m A B D 4m 4m x V V kN A A = = 7 (↑) ( ) 0 == ↑ 5 V V kN B B 0 6 H kN MC f VA VB = = H H 0 QQ H = − cos sin ϕ ϕ 0 NQ H = + sin cos ϕ ϕ 0 截面D的几何参数： MM H = − y 3 Dy = m sin 0.447 ϕ D = − cos 0.894 ϕ D = 0 = −1 左 Q kN D 0 = −5 右 Q kN D 3-6 三铰拱 示例 (2) 内力的计算 4m C D 1 /m kN 4kN y 6 6 0 = ⋅ 2 M kN m D 2kN m 1.79kN 1.79kN 5.81kN 7.61kN = ⋅ = =− = = 左 右 左 右 D D D D D M Q Q N N ( ) 2 4 f y xl x l = − 4m 8m A B D 4m 4m x 7 6 6 5

2013-6-253-6三铰拱示例3-6三铰拱示例（3）内力图.79(3)内力图0.490.400.40.701.792m2ml2m/2m/2m/2m/2m/2m8F图（单位kN）M图（单化kNm）FIN-hISKNF%图（单位kN)8BM单KN.mM ()3-6三铰拱3-6三铰拱合理轴线y(x)=H2.合理轴线例：试求图示三铰拱的合理拱轴线。在给定的荷载作用下，拱上各截面的弯矩均为零mM_gM=M°-HyH:&B.f8f19T0.5L0.51M°(x)=sqtr-MoM(x)V=y(x)HH(t)-x(-t)O3-6三铰拱合理轴线3-7静定结构的基本特征均匀分布的水压力，合理轴线是园弧曲线。教学目标：■理解静定结构的受力特点和分析方法；填土荷载，填土表面为一水平面，合理轴线是悬链线。■掌握静定结构的基本特征。qq=q+yy+ ()-4.chE-x+B-sh.-VH(e =shx+chxe**=chx-shx)58

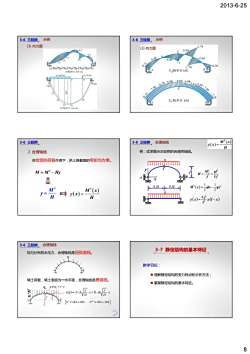
2013-6-25 8 3-6 三铰拱 示例 (3) 内力图 3-6 三铰拱 示例 (3) 内力图 在给定的荷载作用下，拱上各截面的弯矩均为零。 0 M = − M Hy 3-6 三铰拱 2. 合理轴线 0 M y H = ( ) ( ) 0 M x y x H = 例：试求图示三铰拱的合理拱轴线。 f A B C q y 0 2 8 MC ql H f f = = 3-6 三铰拱 合理轴线 ( ) ( ) 0 M x y x H = q 0.5l A B 0.5l x f f 8 ( ) 0 2 1 1 2 2 M x qlx qx = − ( ) ( ) 2 4 = − f yx xl x l 均匀分布的水压力，合理轴线是园弧曲线。 q 填土荷载 填土表面为 水平面 合理轴线是悬链线 3-6 三铰拱 合理轴线 填土荷载，填土表面为一水平面，合理轴线是悬链线。 qc q q y c = +γ ⋅ qc+γ.f f x y y y* { } e shx chx e chx shx x x =+ =− − ( ) x H x B sh H y x = A⋅ch ⋅ + ⋅ ⋅ γ γ 教学目标： „ 理解静定结构的受力特点和分析方法； 3-7 静定结构的基本特征 „ 掌握静定结构的基本特征

2013-6-253-6静定结构的基本特征3-6静定结构的基本特征2.静定结构受力分析方法1.静定结构常见形式及受力特点（1）梁和刚架支座反力和内力计算由受弯直杆（梁式杆）组成。隔离体、建立平衡方程的方法（2）桁架和组合结构3.静定结构的基本特征桁架由只受轴力的链杆组成：组合结构由梁式杆和链杆组成。几何构造：无多余约束（3）三铰拱静力平衡：平衡条件可确定唯一解竖向荷载作用下有水平支座反力的结构。3-6 静定结构的基本特征3-6静定结构的基本特征（1）支座移动、制造误差和温度改变等因素在静定结构（2）静定结构的局部平衡特性中不引起内力。S仔(a)(b) B(b)3(a)BY支座B下沉图(a)中梁AB是几何不图(b)中杆AB承受任杆AC稍有缩短变部分，它自身与荷载意平衡力系时，只有杆ALA维持平衡，因而梁BC无AB产生内力，其余各杆(e)+1内力。都是零杆。杆AB温度改变3-6静定结构的基本特征3-6静定结构的基本特征（3）静定结构的荷载等效性（4）静定结构的构造变换特性图(a)中的荷载F与图(b)中的荷a图(a)杆AB改为一个()载是等效荷载。二者只有杆AB小桁架图(b)。的内力不同，其余各杆的内力都相同。Pe17只是AB的内力有改变，T其余部分的内力没变化。F(6)如图(c)、(d)所示。由局部平衡特性有(a)内力=(b)内力+(c)内力0当静定结构的一个内部几何不变部分作构造变换时其余部分的内力不变。59

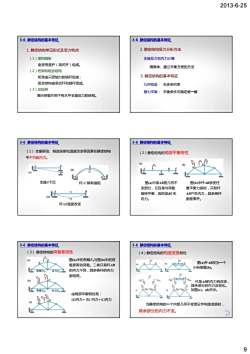
2013-6-25 9 （1）梁和刚架 由受弯直杆（梁式杆）组成。 （2）桁架和组合结构 1. 静定结构常见形式及受力特点 3-6 静定结构的基本特征 桁架由只受轴力的链杆组成； 组合结构由梁式杆和链杆组成。 （3）三铰拱 竖向荷载作用下有水平支座反力的结构。 隔离体、建立平衡方程的方法 2. 静定结构受力分析方法 支座反力和内力计算 静定结构的基本特征 3-6 静定结构的基本特征 几何构造： 无多余约束 静力平衡： 平衡条件可确定唯一解 3. 静定结构的基本特征 （1） 支座移动、制造误差和温度改变等因素在静定结构 中不引起内力。 3-6 静定结构的基本特征 支座B下沉 杆AC稍有缩短 杆AB温度改变 （2）静定结构的局部平衡特性 3-6 静定结构的基本特征 图(a)中梁AB是几何不 变部分，它自身与荷载 维持平衡，因而梁BC无 内力。 图(b)中杆AB承受任 意平衡力系时，只有杆 AB产生内力，其余各杆 都是零杆。 （3） 静定结构的荷载等效性 图(a)中的荷载FP与图(b)中的荷 载是等效荷载。二者只有杆AB 的内力不同，其余各杆的内力 都相同。 3-6 静定结构的基本特征 由局部平衡特性有： (a)内力= (b) 内力+(c)内力 （4）静定结构的构造变换特性 图(a)杆AB改为一个 小桁架图(b)。 3-6 静定结构的基本特征 只是AB的内力有改变， 其余部分的内力没变化。 如图(c)、(d)所示。 当静定结构的一个内部几何不变部分作构造变换时， 其余部分的内力不变

2013-6-255.作业刚架结构：3-7a;3-8c; 3-9b》下一章内容桁架结构：3-17a、d第4章影响线组合结构：3-19a ;三铰拱：3-2110

2013-6-25 10 5. 作业 刚架结构： 3-7a；3-8c；3-9b 桁架结构： 3-17a、d 组合结构： 3-19a； 三铰拱： 3-21 ¾ 下一章内容 第 4 章 影响线