《结构力学》课程授课教案（讲义）第二章 结构的几何构造分析 2.2 平面几何不变体系的组成规律

教学要求熟练掌握几何不变体系的三条基本组成规律。2.2.1一个点与一个刚片的联结方式一二元体法则个刚片与一个点用两根链杆相连，且三个铰不在一直线上，则所组成几何不变体系，并且没有多余约束。说明：以下把研究的对象简称"对象”，对象之间的联系简称"联系”。BO(12BOOC图2-7a几何不变无多余约束图2-76瞬变分析：图2-7a：对象：刚片（1）与点A；联系：链杆1和2；且A、B、C不共线。特例：三个铰共线，则是瞬变体系。图2-7b:对象：刚片（1）与点A：联系：链杆1和2；但A、B、C不共线。例：图2-8分析：图2-8对象：刚片（1）与点A；联系：链杆1和2；且A、B、C不共线。一组成大刚片1对象：大刚片1与点B；联系：链杆3和4；且A、C、D不共线。一组成大刚片2其他同理，见图2-8的图形描述。引伸：二元体：单铰相连且不在同一直线上的两根链杆。如图2-8a中的1、2杆；3、4杆；5、6杆；7、8杆；9、10杆；11、12杆；。二元体的性质：在一个体系上增加或减少1个二元体，不影响原体系的几何组成。图2-8中，图a）、b）、c）、d）、e）、f）的几何组成是相同的，从图a）～图f）为增加二元体；从图f）～图a）为减少二元体。2.2.2两个刚片之间的联结方式一一两刚片法则（1）两个刚片用一个铰和一根链杆相连结，且三个铰不在一直线上，则所组成几何不变体系，并且没有多余约束

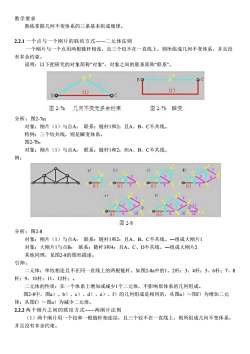
教学要求 熟练掌握几何不变体系的三条基本组成规律。 2.2.1 一个点与一个刚片的联结方式——二元体法则 一个刚片与一个点用两根链杆相连，且三个铰不在一直线上，则所组成几何不变体系，并且没 有多余约束。 说明：以下把研究的对象简称"对象"，对象之间的联系简称"联系"。 分析：图2-7a： 对象：刚片（1）与点A； 联系：链杆1和2；且A、B、C不共线。 特例：三个铰共线，则是瞬变体系。 图2-7b： 对象：刚片（1）与点A； 联系：链杆1和2；但A、B、C不共线。 例： 分析：图2-8 对象：刚片（1）与点A； 联系：链杆1和2；且A、B、C不共线。―组成大刚片1 对象：大刚片1与点B； 联系：链杆3和4；且A、C、D不共线。―组成大刚片2 其他同理，见图2-8的图形描述。 引伸： 二元体：单铰相连且不在同一直线上的两根链杆。如图2-8a中的1、2杆；3、4杆；5、6杆；7、8 杆；9、10杆；11、12杆；。 二元体的性质：在一个体系上增加或减少1个二元体，不影响原体系的几何组成。 图2-8中，图a）、b）、c）、d）、e）、f）的几何组成是相同的，从图a）～图f）为增加二元 体；从图f）～图a）为减少二元体。 2.2.2 两个刚片之间的联结方式——两刚片法则 （1）两个刚片用一个铰和一根链杆相连结，且三个铰不在一直线上，则所组成几何不变体系， 并且没有多余约束

C211图2-9几何不变无多余约束分析：图2-9对象：刚片（1）与（2）；联系：链杆1和铰A；且A、B、C不共线。特例：三个铰共线，瞬变体系。06aC2J(1)(1)图2-10瞬变体系分析：图2-10对象：刚片：（1）与大地：联系：链杆1和铰A：且不共线一一组成大刚片（2）。对象：大刚片（2）与刚片（3）；联系：链杆2和铰B；但共线。（2）两刚片三链杆对象：刚片（1）与（2）；联系：链杆1、2和3。a）三链杆不共点，且不平行，几何不变体系（图2-11a）。OmAm图2-11特例：三链杆平行等长：常变体系（图2-11b）；三链杆平行不等长：瞬变体系（图2-11c）；b）三链杆共点：常变体系（图2-12a）；

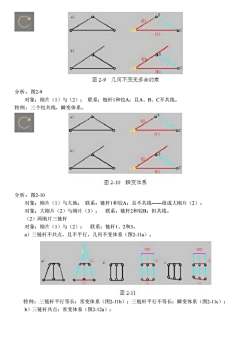
分析：图2-9 对象：刚片（1）与（2）； 联系：链杆1和铰A；且A、B、C不共线。 特例：三个铰共线，瞬变体系。 分析：图2-10 对象：刚片（1）与大地； 联系：链杆1和铰A；且不共线――组成大刚片（2）。 对象：大刚片（2）与刚片（3）； 联系：链杆2和铰B；但共线。 （2）两刚片三链杆 对象：刚片（1）与（2）； 联系：链杆1、2和3。 a）三链杆不共点，且不平行，几何不变体系（图2-11a）。 特例：三链杆平行等长：常变体系（图2-11b）；三链杆平行不等长：瞬变体系（图2-11c）； b）三链杆共点：常变体系（图2-12a）；

不不图2-12特例：延长线交于一点：瞬变体系（图2-12b）；2.2.3三个刚片之间的联结方式三刚片法则三刚片用不共线的三铰两两相连组成体系几何不变且无多余约束。C图2-13几何不变无多余约束分析：图2-13a和b对象：刚片（1）、（2）与（3）；联系：刚片（1）和（2）铰A：刚片（1）和（3）铰B刚片（2）和（3）铰C：且三铰不共线。分析：图2-13c对象：刚片（1）、（2）与（3）；联系：刚片（1）和（2）铰A（虚铰，杆1、2延长线的交点）；刚片（1）和（3）铰B：刚片（2）和（3）铰C；且三铰不共线。分析：图2-13d对象：刚片（1）、（2）与（3）；联系：刚片（1）和（2）铰A（虚铰，杆5、6延长线的交点）；刚片（1）和（3）铰B（虚铰杆1、2延长线的交点）：刚片（2）和（3）铰C（虚铰，杆3、4延长线的交点）：且三铰不共线。特例：若三铰共线，则为瞬变体系2)S图2-14瞬变体系分析：图2-13a和b对象：刚片（1）、（2）与（3）；联系：刚片（1）和（2）铰A；刚片（1）和（3）铰B；刚片（2）和（3）铰C；但三铰共线

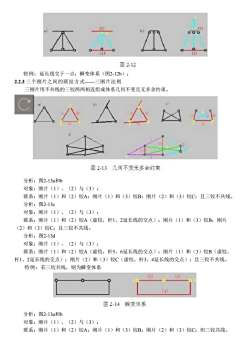
特例：延长线交于一点：瞬变体系（图2-12b）； 2.2.3 三个刚片之间的联结方式——三刚片法则 三刚片用不共线的三铰两两相连组成体系几何不变且无多余约束。 分析：图2-13a和b 对象：刚片（1）、（2）与（3）； 联系：刚片（1）和（2）铰A；刚片（1）和（3）铰B；刚片（2）和（3）铰C；且三铰不共线。 分析：图2-13c 对象：刚片（1）、（2）与（3）； 联系：刚片（1）和（2）铰A（虚铰，杆1、2延长线的交点）；刚片（1）和（3）铰B；刚片 （2）和（3）铰C；且三铰不共线。 分析：图2-13d 对象：刚片（1）、（2）与（3）； 联系：刚片（1）和（2）铰A（虚铰，杆5、6延长线的交点）；刚片（1）和（3）铰B（虚铰， 杆1、2延长线的交点）；刚片（2）和（3）铰C（虚铰，杆3、4延长线的交点）；且三铰不共线。 特例：若三铰共线，则为瞬变体系 分析：图2-13a和b 对象：刚片（1）、（2）与（3）； 联系：刚片（1）和（2）铰A；刚片（1）和（3）铰B；刚片（2）和（3）铰C；但三铰共线

[注意11.三铰为两两相交的铰：2.所有规则可以统一为三角形法则：由三个链杆组成的三角形为几何不变体系且无多余约束。2.2.4基本分析方法1.组装法规律：一点、两片、三片、三链杆：基本装配格式：固定一个结点：固定一个刚片：固定两个刚片：固定三个刚片：（1）从基础开始例1：(2)BRH图2-15分析：对象：刚片（1）与大地；联系：铰A和链杆1且三铰不共线；一一组成大刚片1对象：大刚片1与刚片（2）：联系：铰B和链杆2且三铰不共线：一组成大刚片2对象：大刚片2与刚片（3）；联系：铰C和链杆3且三铰不共线；一一几何不变无多余约束（2）从内部开始例2：图2-16分析：对象：刚片（1）与（2）（三角形法则）；联系：铰A和链杆1且三铰不共线；一组成大刚片1；对象：大刚片1与大地；联系：铰B和链杆2且三铰不共线；一一几何不变无多余约束（3）减二元体例3：图2-17分析：对象：杆1、2和杆3、4和杆5、6和杆7、8和杆9、10和杆11、12和杆13、14；联系：二元体：去掉二元体，剩下大地几何不变无多余约束

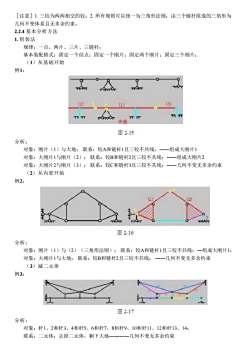
［注意］1. 三铰为两两相交的铰；2. 所有规则可以统一为三角形法则：由三个链杆组成的三角形为 几何不变体系且无多余约束。 2.2.4 基本分析方法 1. 组装法 规律：一点、两片、三片、三链杆； 基本装配格式：固定一个结点；固定一个刚片；固定两个刚片；固定三个刚片； （1）从基础开始 例1： 分析： 对象：刚片（1）与大地； 联系：铰A和链杆1且三铰不共线；――组成大刚片1 对象：大刚片1与刚片（2）； 联系：铰B和链杆2且三铰不共线；――组成大刚片2 对象：大刚片2与刚片（3）； 联系：铰C和链杆3且三铰不共线；――几何不变无多余约束 （2）从内部开始 例2： 分析： 对象：刚片（1）与（2）（三角形法则）； 联系：铰A和链杆1且三铰不共线；―组成大刚片1； 对象：大刚片1与大地； 联系：铰B和链杆2且三铰不共线； ――几何不变无多余约束 （3）减二元体 例3： 分析： 对象：杆1、2和杆3、4和杆5、6和杆7、8和杆9、10和杆11、12和杆13、14； 联系：二元体；去掉二元体，剩下大地――――几何不变无多余约束

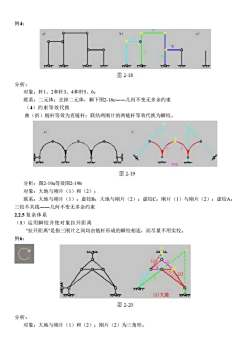
例4：r图2-18分析：对象：杆1、2和杆3、4和杆5、6；联系：二元体；去掉二元体，剩下图2-16c一一几何不变无多余约束（4）约束等效代换曲（折）链杆等效为直链杆：联结两刚片的两链杆等效代换为瞬铰。图2-19分析：图2-19a等效图2-19b对象：大地与刚片（1）和（2）：联系：大地与刚片（1）：虚铰B；大地与刚片（2）：虚铰C；刚片（1）与刚片（2）：虚铰A；三铰不共线一一几何不变无多余约束2.2.5复杂体系（1）运用瞬铰并使对象拉开距离"拉开距离"是指三刚片之间均由链杆形成的瞬铰相连，而尽量不用实铰。例6：CO（3）大地-图2-20分析：对象：大地与刚片（1）和（2）：刚片（2）为三角形

例4： 分析： 对象：杆1、2和杆3、4和杆5、6； 联系：二元体；去掉二元体，剩下图2-16c――几何不变无多余约束 （4）约束等效代换 曲（折）链杆等效为直链杆；联结两刚片的两链杆等效代换为瞬铰。 分析：图2-19a等效图2-19b 对象：大地与刚片（1）和（2）； 联系：大地与刚片（1）：虚铰B；大地与刚片（2）：虚铰C；刚片（1）与刚片（2）：虚铰A； 三铰不共线――几何不变无多余约束 2.2.5 复杂体系 （1）运用瞬铰并使对象拉开距离 "拉开距离"是指三刚片之间均由链杆形成的瞬铰相连，而尽量不用实铰。 例6： 分析： 对象：大地与刚片（1）和（2）；刚片（2）为三角形

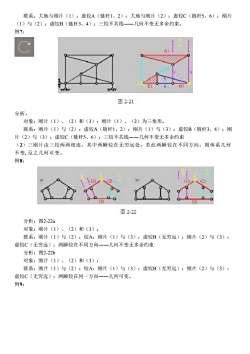
联系：大地与刚片（1）：虚铰A（链杆1、2）：大地与刚片（2）：虚铰C（链杆5、6）：刚片（1）与（2）：虚铰B（链杆3、4）；三铰不共线一一几何不变无多余约束。例7：C图2-21分析：对象：刚片（1）、（2）和（3）：刚片（1）、（2）为三角形联系：刚片（1）与（2）：虚铰A（链杆1、2）；刚片（1）与（3）：虚铰B（链杆3、4）：刚片（2）与（3）：虚铰C（链杆5、6）：三铰不共线一一几何不变无多余约束（2）三刚片由三铰两两相连，其中两瞬铰在无穷远处。若此两瞬铰在不同方向，则体系几何不变，反之几何可变。例8：图2-22分析：图2-22a对象：刚片（1）、（2）和（3）；联系：刚片（1）与（2）：铰A；刚片（1）与（3）：虚铰B（无穷远）；刚片（2）与（3）：虚铰C（无穷远）：两瞬铰在不同方向一一几何不变无多余约束分析：图2-22b对象：刚片（1）、（2）和（3）；联系：刚片（1）与（2）：铰A；刚片（1）与（3）：虚铰B（无穷远）；刚片（2）与（3）：虚铰C（无穷远）；两瞬铰在同一方向一一几何可变。例9：

联系：大地与刚片（1）：虚铰A（链杆1、2）；大地与刚片（2）：虚铰C（链杆5、6）；刚片 （1）与（2）：虚铰B（链杆3、4）；三铰不共线――几何不变无多余约束。 例7： 分析： 对象：刚片（1）、（2）和（3）；刚片（1）、（2）为三角形。 联系：刚片（1）与（2）：虚铰A（链杆1、2）；刚片（1）与（3）：虚铰B（链杆3、4）；刚 片（2）与（3）：虚铰C（链杆5、6）；三铰不共线――几何不变无多余约束 （2）三刚片由三铰两两相连，其中两瞬铰在无穷远处。若此两瞬铰在不同方向，则体系几何 不变, 反之几何可变。 例8： 分析：图2-22a 对象：刚片（1）、（2）和（3）； 联系：刚片（1）与（2）：铰A；刚片（1）与（3）：虚铰B（无穷远）；刚片（2）与（3）： 虚铰C（无穷远）；两瞬铰在不同方向――几何不变无多余约束 分析：图2-22b 对象：刚片（1）、（2）和（3）； 联系：刚片（1）与（2）：铰A；刚片（1）与（3）：虚铰B（无穷远）；刚片（2）与（3）： 虚铰C（无穷远）；两瞬铰在同一方向――几何可变。 例9：

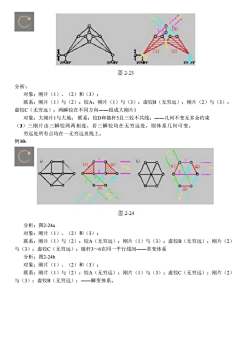
C图2-23分析：对象：刚片（1）、（2）和（3）；联系：刚片（1）与（2）：铰A；刚片（1）与（3）：虚铰B（无穷远）：刚片（2）与（3）：虚铰C（无穷远）；两瞬铰在不同方向一一组成大刚片1对象：大刚片1与大地：联系：铰D和链杆5且三铰不共线：一一几何不变无多余约束（3）三刚片由三瞬铰两两相连，若三瞬铰均在无穷远处，则体系几何可变。穷远处所有点均在一无穷远直线上。例10：C图2-24分析：图2-24a对象：刚片（1）、（2）和（3）；联系：刚片（1）与（2）：铰A（无穷远）；刚片（1）与（3）：虚铰B（无穷远）；刚片（2）与（3）：虚铰C（无穷远）；链杆3～6在同一平行线间一一常变体系分析：图2-24b对象：刚片（1）、（2）和（3）；联系：刚片（1）与（2）：铰A（无穷远）；刚片（1）与（3）：虚铰C（无穷远）；刚片（2）与（3）：虚铰B（无穷远）：一一瞬变体系

分析： 对象：刚片（1）、（2）和（3）； 联系：刚片（1）与（2）：铰A；刚片（1）与（3）：虚铰B（无穷远）；刚片（2）与（3）： 虚铰C（无穷远）；两瞬铰在不同方向――组成大刚片1 对象：大刚片1与大地； 联系：铰D和链杆5且三铰不共线；――几何不变无多余约束 （3）三刚片由三瞬铰两两相连，若三瞬铰均在无穷远处，则体系几何可变。 穷远处所有点均在一无穷远直线上。 例10： 分析：图2-24a 对象：刚片（1）、（2）和（3）； 联系：刚片（1）与（2）：铰A（无穷远）；刚片（1）与（3）：虚铰B（无穷远）；刚片（2） 与（3）：虚铰C（无穷远）；链杆3～6在同一平行线间――常变体系 分析：图2-24b 对象：刚片（1）、（2）和（3）； 联系：刚片（1）与（2）：铰A（无穷远）；刚片（1）与（3）：虚铰C（无穷远）；刚片（2） 与（3）：虚铰B（无穷远）；――瞬变体系