《结构力学》课程教学资源（课件讲稿）第六章 力法

第6章力法教学目标：第6章力法■正确判断超静定结构的次数；■理解力法方程的物理意义；ForceMethod■掌握力法的基本概念及解题步骤；..■应用力法计算荷载作用下超静定结构的内力：联■了解温度变化时的内力计算。6-1超静定结构的组成和超静定的次数第6章力法教学内容：几何不变体系且有多余约束6-1超静定结构的组成和超静定的次数6-2力法的基本概念内力及反力无法由平衡条件得到全部求解6-3/4力法解超静定结构6-5 对称结构的计算6-8支座移动和温度改变时的计算6-9超静定结构的位移计算22.超静定结构的解法1.超静定结构的类型（1）超静定梁T综合考虑二个方面的条件：XIX（2）超静定桁架（1）平衡条件；（2）几何条件；（3）超静定拱具体求解时，有两种基本（经典)方法：（4）超静定刚架力法和位移法。（5）超静定组合结构

1 Force Method 第 6 章 力 法 Force Method 第 6 章 力 法 „ 正确判断超静定结构的次数； „ 理解力法方程的物理意义； 教学目标： „ 掌握力法的基本概念及解题步骤； „ 应用力法计算荷载作用下超静定结构的内力； „ 了解温度变化时的内力计算。 第 6 章 力 法 教学内容： 6-1 超静定结构的组成和超静定的次数 6-2 力法的基本概念 6-3/4 力法解超静定结构 6-5 对称结构的计算 6-8 支座移动和温度改变时的计算 6-9 超静定结构的位移计算 6-1 超静定结构的组成和超静定的次数 几何不变体系且有多余约束 内力及反力无法由平衡条件得到全部求解 （1）超静定梁 （2）超静定桁架 1. 超静定结构的类型 （4）超静定刚架 （5）超静定组合结构 （3）超静定拱 综合考虑二个方面的条件: （1）平衡条件； （2）几何条件； 2. 超静定结构的解法 （2）几何条件； 具体求解时，有两种基本(经典)方法： 力法和位移法

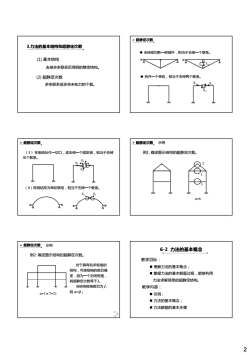
>超静定次数3.力法的基本结构和超静定次数◆去掉或切断一根链杆，相当于去掉一个联系，(1)基本结构去掉多余联系后得到的静定结构。●拆开一个单铰，相当于去掉两个联系。(2)超静定次数X多余联系或多余未知力的个数。>超静定次数>超静定次数示例（3）在刚结处作一切口，或去掉一个固定端，相当于去掉例1：确定图示结构的超静定次数。三个联系。LX.（4）将刚结改为单铰联结，相当于去掉一个联系。Xn=6超静定次数。示例6-2力法的基本概念例2：确定图示结构的超静定次数。教学目标：对于具有较多框格的■理解力法的基本概念；结构，可按框格的数目确■掌握力法的基本解题过程，能够利用定，因为一个封闭框格，力法求解简单的超静定结构。其超静定次数等于3。当结构框格数目为于，教学内容：则n=3f。n=3 × 7=21■引例；■力法的基本概念；■力法解题的基本步骤D2

2 (1) 基本结构 去掉多余联系后得到的静定结构。 3.力法的基本结构和超静定次数 (2) 超静定次数 多余联系或多余未知力的个数。 ‹ 去掉或切断一根链杆，相当于去掉一个联系。 ↓ ↑X1 ¾ 超静定次数 ‹ 拆开一个单铰，相当于去掉两个联系。 1 ←↓↑→ X X1 X2 （3） 在刚结处作一切口，或去掉一个固定端，相当于去掉 三个联系。 ← ↓ X3 X1 X2 ←↓ ¾ 超静定次数 （4）将刚结改为单铰联结，相当于去掉一个联系。 X1 X1 例1: 确定图示结构的超静定次数。 2 1 ¾ 超静定次数 示例 n=6 3 对于具有较多框格的 结构，可按框格的数目确 定，因为一个封闭框格， 其超静定次数等 例2: 确定图示结构的超静定次数。 ¾ 超静定次数 示例 n=3×7=21 其超静定次数等于3。 当结构框格数目为 f , 则 n=3f 。 教学目标： „ 理解力法的基本概念； „ 掌握力法的基本解题过程，能够利用 力法求解简单的超静定结构 6-2 力法的基本概念 。 教学内容： „ 引例； „ 力法的基本概念； „ 力法解题的基本步骤

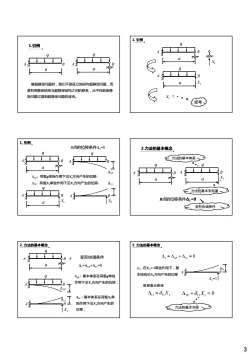
1. 引例1.引例7X7解超静定问题时，我们不是孤立地研究超静定问题，而是利用静定结构与超静定结构之间的联系，从中找到由静定问题过渡到超静定问题的途径1.引例B点的位移条件A,=02.力法的基本概念二力法的基本体系一$Bo.q79aBAAiP4Aip：荷载q单独作用下沿X,方向产生的位移：XX70A：荷载x,单独作用下沿X,方向产生的位移AuD力法的基本未知量一BBLB点的位移条件A;=0X.三变形协调条件2.力法的基本概念2.力法的基本概念A, = Ap +Au = 0变形协调条件BAA,=ip+A=0sm：在x,=1单独作用下，基113：本结构沿X,方向产生的位移Aip：基本体系在荷载q单独X,=1作用下沿X，方向产生的位移；根据叠加原理AIPAp+8,X, =0Au=OuX,An：基本体系在荷载X,单A独作用下沿X,方向产生的B力法的基本方程Xi位移；3

3 q a q a A B A B 1.引例 解超静定问题时，我们不是孤立地研究超静定问题，而 是利用静定结构与超静定结构之间的联系，从中找到由静 定问题过渡到超静定问题的途径。 q a X1 A B q 1. 引例 X1 ? a A B X1 思考 A B q a B点的位移条件Δ1=0 A B Δ1P Δ ：荷载q单独作用下沿X 方向产生的位移； q 1. 引例 q a X1 A B A B Δ11 X1 Δ1P：荷载q单独作用下沿X1方向产生的位移； Δ11：荷载X1单独作用下沿X1方向产生的位移； q X A B 力法的基本体系 q A B 2.力法的基本概念 a a X1 B点的位移条件Δ1=0 力法的基本未知量 变形协调条件 a A q A B 变形协调条件 q Δ1P：基本体系在荷载q单独 Δ1=Δ1P+Δ11=0 2. 力法的基本概念 A B Δ1P A B Δ11 X1 作用下沿X1方向产生的位移； Δ11：基本体系在荷载X1单 独作用下沿X1方向产生的 位移； 0 Δ1 = Δ1P + Δ11 = δ11 : 在X1＝1单独作用下，基 本结构沿X1方向产生的位移 A B δ11 X1=1 2. 力法的基本概念 Δ11 11 1 = δ X 1 11 1 0 Δ+ = P δ X 力法的基本方程 根据叠加原理 X1 1

3.力法解题的基本步骤3.力法解题的基本步骤（3）作出基本结构的Ap+8,X, =0q荷载弯矩图，单位弯矩图0.5qAAB（4）求出系数和自由项a一单位荷载法MpgaMQA14（1）确定基本体系Ap =P61"3EIA8EI一确定基本未知量Xa1-A_3M,X, =-ggX为正值，说明基本未知量的方向（2）根据位移协调条件（5）解力法方程Ap+8uX =0一写出力法基本方程与假设方向相同；如为负值，则方一求解基本未知量向相反。3.力法解题的基本步骤二次超静定q0.5qaBA1-B[ PPMpXaA1c&dBBBcXX,=qaa18M,BcXi-qaMxiAA（6）叠加法作弯矩图990Lqa++p=0M=MX+M018.4Bm+0+p=0MN次超静定系数和自由项》梁、刚架：8X,+,X,+.+o.X,+Ap=0--X+8X+...+8.X.+Ap=0M,MpdsEIEIAp=ZAJEI0-2SX,+S.X,+...+S.X+A.p=0AEI》桁架：M= MX +M.X,+.+M.X.+M,-N=NiX,+N2X,+.+N.X+NpEAAP-NNN,N,EA0-EJR-RiX,+R2X,+..+R.X.+RpEA54

4 a A B q q 3.力法解题的基本步骤 （2）根据位移协调条件 —写出力法基本方程 1 11 1 0 Δ P + = δ X （1）确定基本体系 —确定基本未知量 a X1 A B q 1 11 1 0 Δ+ = P δ X A B MP 0.5qa2 （3）作出基本结构的 荷载弯矩图，单位弯矩图 （4）求出系数和自由项 —单位荷载法 3. 力法解题的基本步骤 A B 1 M1 a 3 11 3 a EI δ = 4 1 8 P qa EI Δ =− 1 1 11 3 8 P X qa δ Δ =− = X1为正值，说明基本未知量的方向 与假设方向相同；如为负值，则方 向相反。 （5）解力法方程 —求解基本未知量 1 3 8 X = qa A B A B MP a 1 0.5qa q 2 a A B 3. 力法解题的基本步骤 （6）叠加法作弯矩图 M = + MX M 1 1 P 8 1 M1 a MX1 3 2 8 qa A B M 1 2 8 qa 1 2 8 qa 1 3 8 X = qa 0 B C X1 X2 P B C P 二次超静定 A 11 1 12 2 1 0 P δ x x +δ +Δ = 21 1 22 2 2 0 P δ x x +δ +Δ = A 11 1 12 2 1n 1 21 1 22 2 2n 2 X X . X 0 X X . X 0 . XX X 0 n P n P δδ δ δδ δ δδ δ + + + +Δ = ⎫ ⎪ + + + +Δ = ⎪ ⎬ ⎪ + + + +Δ ⎪ ⎭ N 次超静定 11 2 2 n X X . X 0 n n n n nP δδ δ + + + +Δ = ⎪ ⎭ n P M = M1X1 + M2X2 + .+ MnX + M n P N = N1X1 + N2X2 + .+ NnX + N n P R = R1X1 + R2X2 + .+ RnX + R 系数和自由项 ¾ 梁、刚架： δii ds EI Mi ∑ ∫ = 2 Ai i y EI = ∑ ds EI Mi M j ∑ ∫ = A yj i δij = ∑ ∑ ∫ = EI M M ds i P ΔiP ¾ 桁架： EI ∑ ∫ EI ij ∑ ∑ ∫ = EA N l i 2 ∑ ∫ = EA N N l i j δii δij ∑ ∫ = EA N N l i P ΔiP

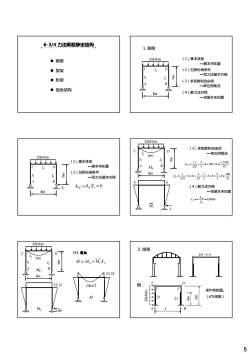
6-3/4力法解超静定结构1.刚架（1）基本体系20kN/m■刚架一基本未知量D（2）位移协调条件1■排架一写力法基本方程6■桁架（3）求系数和自由项B一单位荷载法■组合结构88（4）解力法方程8m一求基本未知量20kN/m（3）求系数和自由项D一单位荷载法16020kN/m12（1）基本体系2560-1.2★★★★×8×160×6=AipB一基本未知量2E13EICDMp11o（2）位移协调条件8m215××6-2881×6×6x×6×8+8. =一写力法基本方程2EIEI*2EIB66A1p +0X, = 0（4）解力法方程d0-0- Xi8m一求基本未知量_Au =8.89kNX, =-ouM,-120kN/m量量2.排架(5）叠加EA→1160M=M+M,X,126Mp53.3368m53.33例：106.67+求作弯矩图。u/EN（E为常数）21Mut21doBAM,8.89-005

5 „ 刚架 „ 排架 6-3/4 力法解超静定结构 „ 桁架 „ 组合结构 C I D 1 20kN/m （1）基本体系 —基本未知量 （2）位移协调条件 写力法基本方程 1. 刚架 8m I2 6m A B I2 —写力法基本方程 （3）求系数和自由项 —单位荷载法 （4）解力法方程 —求基本未知量 6 I m 2 C I D 1 I2 20kN/m （1）基本体系 —基本未知量 （2）位移协调条件 写力法基本方程 8m 2 6 A B I2 —写力法基本方程 X1 1 11 1 0 Δ P + = δ X 8m I2 6m A C D B I1 I2 20kN/m （3）求系数和自由项 —单位荷载法 MP 160 EI EI P 2560 8 160 6 3 2 2 1 1 − × × × × = − Δ = 288 6 2 6 6 2 1 6 8 1 δ 11 = × × + × × × × × = （4）解力法方程 —求基本未知量 M1 1 6 6 2EI EI 2 3 EI 11 X kN P 8.89 11 1 1 = Δ = − δ 8m I2 6m A C D B I1 I2 20kN/m （5）叠加 MP 160 53.33 M = MP + M1X1 M1 8.89 53.33 106.67 M EA → ∞ 2. 排架 l 6m A C D B 20kN/m 2I 4m I 2I I 例： 求作弯矩图。 （E为常数）

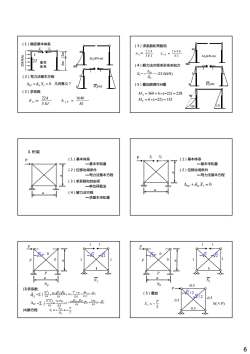
（1）确定基本体系（3）求系数和常数项X.X22416408u=AP=?3E1EIEM,(kN-m)U/NYOM,(kN-m)+21基本2（4）解力法方程求多余未知力体系_ --22.0(kN)X-（2）写力法基本方程onA+X=0几何意义？M,(m)（5）叠加原理作M图M,(m)（3）求系数M,=360+6x(-22)=2282241640M=6x(-22)=1328.=AIPE3EIEI3.桁架（1）基本体系（1）基本体系1一基本未知量一基本未知量（2）位移协调条件（2）位移协调条件一写力法基本方程一写力法基本方程（3）求系数和自由项Ap+SX,=0一单位荷载法O（4）解力法方程一求基本未知量PdaNNpNp-0.5(3)求系数D1xa.(+/2)_2-VP+4X212（5）叠加S.-EEFEA121-0.50.51xPax2+5x-Ea-2Pa(1+V2)PAp=[X, =-N(XP)E4EAEAX,--A.-P(4)解方程on6

6 1 1 2m 20kN/m 4m I 2I 基本 体系 （1）确定基本体系 360 40 (kN⋅m) MP X1 X1 1 11 1 0 Δ+ = P δ X （2）写力法基本方程 几何意义？ M1 6 (m) 2 （3）求系数 EI EI P 1640 3 224 δ 11＝ Δ 1 = 1 1 360 40 (kN⋅m) MP 2 （3）求系数和常数项 11 1P 224 1640 3EI EI δ ＝ Δ = （4）解力法方程求多余未知力 22 0(kN) 1 1 = − Δ − P X ＝ M1 6 (m) 22.0(kN) 2 11 1 δ X （5）叠加原理作M图 6 ( 22) 132 360 6 ( 22) 228 = × − = = + × − = C A M M 132 228 90 P a （1）基本体系 —基本未知量 （2）位移协调条件 —写力法基本方程 3.桁架 a （3）求系数和自由项 —单位荷载法 （4）解力法方程 —求基本未知量 P a （1）基本体系 —基本未知量 （2）位移协调条件 —写力法基本方程 X1 X1 a 1 11 1 0 Δ+ = P δ X P a a 1 1 N 0 P 0 P − 2P − 2 1 1 1 − 2 NP N1 (3)求系数 (4)解方程 δ11 ∑ ∫ = EA N l i 2 2 2( 2) 2a EA − = EA × a + × 2 1 4 (1 2) 4 = + EA a Δ1P ∑ ∫ = EA N N l i j 1 2 Pa EA × = × ( 2)( 2 ) 2 P a EA − − + 2 (1 2) Pa EA = + 1 1 11 2 P P X δ Δ =− =− P a a 1 1 N 0 P 0 P − 2P − 2 1 1 − 2 1 NP N1 1 2 P X = − （5）叠加 − 2/2 P -0.5 N(×P) 0.5 0.5 -0.5 2/2

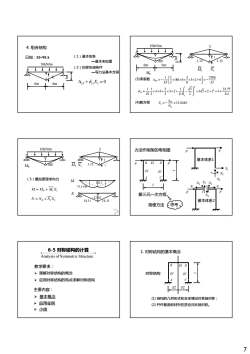
10kN/m4.组合结构（1）基本体系0已知：EI=9EA一基本未知量81801.121.1210kN/m6m6m（2）位移协调条件M,Nttt一写力法基本方程Mp2700(3)求系数Au3×180×6x×3×2+0Ap+X =0EI(306m6m5)23.7711×3/5×2+1×33×6x<3×2+duEI2EAL2EA3_AP=12.62kN(4)解方程X.=10kN/m力法作刚架的弯矩图+★基本体系188UT80M, N,Mp+XX（5）叠加原理求内力XM711M=Mp+M,XV方程解三元N=N,+N,X基本体系214.1114.11（思考）简便方法L6-5对称结构的计算1.对称结构的基本概念Analysisof Symmetric StructureEI教学要求：》理解对称结构的概念对称结构5》应用对称结构的特点求解对称结构711主要内容：》基本概念(1)结构的几何形式和支承情况对某轴对称；》应用实例(2）杆件截面和材料性质也对此轴对称》小结7

7 10kN/m （1）基本体系 —基本未知量 （2）位移协调条件 —写力法基本方程 已知：EI=9EA 4. 组合结构 6m 6m 3m 1 11 1 0 Δ+ = P δ X X1 6m 6m 3m 10kN/m 180 3 1 1.12 1.12 MP M1 N1 1 1 2 5 2700 180 6 3 2 0 3 8 P EI EI ⎛ ⎞ Δ =− × × × × × + =− ⎜ ⎟ ⎝ ⎠ EI EA EA 23.77 3 5 2 1 3 2 1 5 3 2 3 2 3 6 2 1 1 2 2 11 × × + × = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ δ = × × × × × + − 1 1 11 12.62 P X kN δ Δ =− = (3)求系数 (4)解方程 10kN/m M 180 P 1 3 M1 N1 1.12 1 （5）叠加原理求内力 142.1 71.1+45 M 14.11 14.11 N -12.62 M = MP + M1X1 N = NP + N1X1 力法作刚架的弯矩图 l EI EI EI P P A B D C P P 基本体系1 X1 X3 l A C X2 P P 基本体系2 X1 X2 X1 X2 X3 X3 解三元一次方程 简便方法 思考 教学要求： ¾ 理解对称结构的概念 ¾ 应用对称结构的特点求解对称结构 Analysis of Symmetric Structure 6-5 对称结构的计算 主要内容： ¾ 基本概念 ¾ 应用实例 ¾ 小结 l EI EI EI A B D C 对称结构 1. 对称结构的基本概念 l/2 A C l/2 (1) 结构的几何形式和支承情况对某轴对称； (2) 杆件截面和材料性质也对此轴对称

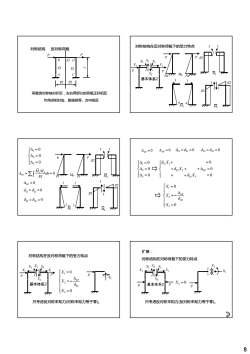
对称结构在反对称荷载下的受力特点对称结构反对称荷载-Pa基本体系2121/2荷载绕对称轴对折后，左右两部分的荷载正好相反作用点相对应、数值相等、方向相反, =(012=021=0023=02=0Aip=0Ap=04, =-(4=0[8.X, +=04=0+8,X,++△2p = 0AP=E[MM,ds=04,=0=0+0mX,EI43p=0X, =0012=021=0--A2pX,=S02282=0,=0X, =0扩展对称结构在反对称荷载下的受力特点对称结构在对称荷载下的受力特点XXXXX14X=0A2F基本体系2基本体系2022X,=07只考虑反对称末知力（对称未知力等于零）只考虑反对称末知力（反对称未知力等于零）S8

8 l EI EI EI A B D C 对称结构 P P 反对称荷载 l/2 A C l/2 荷载绕对称轴对折后，左右两部分的荷载正好相反 作用点相对应、数值相等、方向相反 对称结构在反对称荷载下的受力特点 P P X1 X2 X1 X2 X3 X3 P P M l/2 M3 1 1 基本体系2 X2 MP 1 1 1 1 Pa Pa a a l/2 l/2 M1 M2 3 P P Pl MP Pl l/2 M3 1 1 1 2 3 0 0 0 ⎧Δ = ⎪ ⎨Δ = ⎪ ⎩Δ = 1 1 0 P P M M ds EI Δ= = ∑∫ 1 1 1 1 Pl Pl l l l/2 l/2 M1 M2 EI 3 3 0 Δ = P 12 21 δ = = δ 0 23 32 δ = = δ 0 1 2 3 0 0 0 ⎧Δ = ⎪ ⎨Δ = ⎪ ⎩Δ = 11 1 12 2 13 3 1 21 1 22 2 23 3 2 31 1 32 2 33 3 3 0 0 0 P P P XXX XXX X X X δδ δ δδ δ δ δ δ ⎧ + + +Δ = ⎪ ⎨ + + +Δ = ⎪ ⎩ + + +Δ = 1 0 Δ P = 3 0 Δ P = 12 21 δ = = δ 0 23 32 δ = δ = 0 ⎩ 3 ⎩ 31 1 32 2 33 3 3P 1 2 2 22 3 0 0 P X X X δ ⎧ = ⎪ ⎪ Δ ⎨ = − ⎪ ⎪ ⎩ = P P X1 X2 X1 X2 X3 X3 对称结构在反对称荷载下的受力特点 1 2 0 P ⎧X = ⎪ ⎪ Δ ⎨ P X2 基本体系2 X2 2 2 22 3 0 P X X δ ⎪ Δ ⎨ = − ⎪ ⎪ ⎩ = 只考虑反对称末知力(对称未知力等于零)。 X1 X2 X1 X2 X3 X3 对称结构在对称荷载下的受力特点 扩展： X1 X3 P 基本体系2 P X2 2 X = 0 只考虑反对称末知力(反对称未知力等于零)。 P

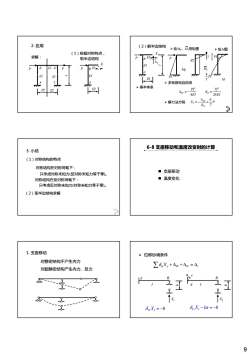
2.应用（2）解半边结构>绘Mp、M弯矩图>绘M图（1）根据对称特点，求解：PREI取半边结构EBEI7,TMMpETPI7712L>求系数和自由项>基本体系PP71312Aip=ou=24EI4EIAr-Sp>解力法方程X,=o726-8支座移动和温度改变时的计算3.小结（1）对称结构的特点对称结构在对称荷载下：■支座移动只考虑对称末知力(反对称未知力等于零)。■温度变化对称结构在反对称荷载下：只考虑反对称末知力（对称未知力等于零）。（2）取半边结构求解21.支座移动》位移协调条件对静定结构不产生内力Zo,X, +Ap +Ac=A,对超静定结构产生内力、反力2B1A1&&&1xIxAS8X,-lα=-bo.X,=-b9

9 P B EI D P 求解： （1）根据对称特点， 取半边结构 P EI B E 2. 应用 l/2 EI l EI A C l/2 l/2 EI A （2）解半边结构 P EI EI A B E X2 P MP l/2 M2 1 ¾ 绘MP、M1弯矩图 l ¾ 绘M图 3 7 Pl 4 l/2 ¾ 基本体系 Pl ¾ 求系数和自由项 3 11 7 24 l EI δ = 3 1 4 P Pl EI Δ =− 1 1 11 6 7 P X P δ Δ ¾ 解力法方程 =− = M 4 7 Pl （1）对称结构的特点 对称结构在对称荷载下： 只考虑对称末知力(反对称未知力等于零)。 3. 小结 （2）取半边结构求解 对称结构在反对称荷载下： 只考虑反对称末知力(对称未知力等于零)。 6-8 支座移动和温度改变时的计算 „ 支座移动 „ 温度变化 对静定结构不产生内力 对超静定结构产生内力、反力 1. 支座移动 ¾ 位移协调条件 ∑δ ij j iP iC i X + Δ +Δ =Δ A B B α X1 δ 11 1 X b = − l b δ 11 1 Xl b − =− α A b X1 l

（2）位移协调条件Z8X, +Ap +Aic =AnBBIX1X9bF8,X,+2X,-a-1β=0,X, +4=0S.X=02,X,+022X, +b+hβ= 02.温度变化》位移协调条件对静定结构不产生内力Zo,X, +Ap+A, =A,对超静定结构产生内力、反力tPugsxt,ds=duA114t>tat,dsR1ATA, =EαtoJ Nds +ZMd,=-15'C f=25'C h=%+1BhC4M.NMN.t,=-15'C,=25'Ch=%13.4F基本体系d8,012=0213EI3EI2EIA,=α.5/+α.400,/28u +o2x+A=0aA195alA.-2Niatl+ZMd=04,=α.51+α-400)=605αl力法方程-10

10 （2）位移协调条件 ∑δ ij j iP iC i X +Δ +Δ =Δ α A b B l X A B l α P 11 1 b X l δ + =α A l b 11 1 1P b X l δ +Δ + =α X1 X1 A l A B C X1 h a b X2 l β 11 1 12 2 δ X X al +δ β −− = 0 21 1 22 2 δ X X bh +δ β ++ = 0 对静定结构不产生内力 对超静定结构产生内力、反力 t1 2. 温度变化 A B t2 t1 t2> t1 A B t2 t1 ¾ 位移协调条件 ∑δ ij j iP it i X + Δ +Δ =Δ 1 αt ds αt ds=du 1t 1 h it 0 t t Nds Mds h α α Δ Δ= + ∑ ∑ ∫ ∫ 2 h ds 2 αt ds dθ 0 αt ds=du 2t h 1 h A B C t l 2 t1 t1 t2 t C D 1 = −15 t C D 25 2 = 10 l h = A B C X2 t2 t1 t2 X1 l 11 1 12 2 1 21 1 22 2 2 0 0 t t x x x x δ δ δ δ ⎧ + +Δ = ⎨ ⎩ + +Δ = i it i t N tl M ds h α α Δ Δ =∑ +∑ ∫ 基本体系 力法方程 A B C 1 l l +1 +1 t C D 1 = −15 t C D 25 2 = 10 l h = M1 N1 A B C 1 M2 N2 3 11 3 l EI δ = 3 12 21 2 l EI δ δ = =− 3 22 4 3 l EI δ = l l l l t α α α ) 195 2 ( 400 5 2 1 − = − ⋅ Δ = ⋅ + 1 2 10 2 2 2 400 5 ( ) 605 2 t l ll l l α α α ⋅ Δ=⋅ + + =