《结构力学》课程教学资源（课件讲稿）第九章 矩阵位移法 9.7 计算步骤和算例

9-7计算步骤和算例教学目标：掌握矩阵位移法计算结构内力。教学内容：计算步骤算例

9-7 计算步骤和算例 教学目标： „ 掌握矩阵位移法计算结构内力。 教学内容： „ 计算步骤 „ 算例

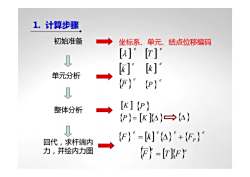
1.计算步骤初始准备单元、坐标系、结点位移编码[a]°[[ ]1[k] [K] 单元分析(P)°(P)八[K] (P]整体分析(P}= [K-()八{F)°=[k]A)"+{F,)回代，求杆端内力，并绘内力图(F =[T(F)

1.  计算步骤 初始准备 单元分析 整体分析 回代，求杆端内 力，并绘内力图 { } [ ] {} { } e P e e e F = k Δ + F 坐标系、单元、结点位移编码 [K ] {P} {P}= [ ] K {Δ} {Δ} { } [ ]{ }e e F = T F [ ] e k [ ] e k { } e { } P e P [ ] e λ [ ] e T

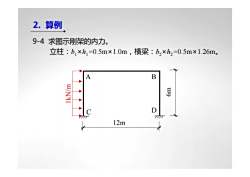
2.算例9-4求图示刚架的内力。立柱：b,×h,=0.5m×1.0m，横梁：bz×hz=0.5m×1.26m。BAW/NYI9D12m

2.  算例 9-4求图示刚架的内力。 立柱：b1×h1=0.5m×1.0m，横梁：b2×h2=0.5m×1.26m。 C D A B 12m 1kN/m

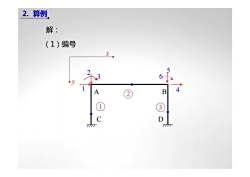
2. 算例解：（1）编号BAODC1T4

x y （1）编号 2 3 1 5 6 4 C D A B 1 2 3 2.  算例 解：

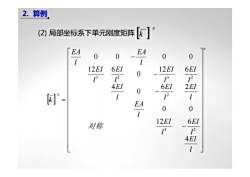
2. 算例[] (2)局部坐标系下单元刚度矩阵EA1EA0000116EI6EI12EI12 EI01213[2134EI6EI2EI02/[] =1EA0016EI12EI对称12134EI1

(2)局部坐标系下单元刚度矩阵 [ ] e k [ ] e e l EI l EI l EI l EA l EI l EI l EI l EI l EI l EI l EI l EA l EA k ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − = 4 12 6 0 0 6 2 0 4 12 6 0 12 6 0 0 0 0 3 2 2 3 2 3 2 对称 2.  算例

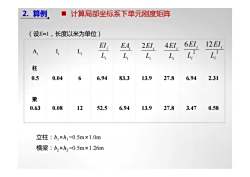
2. 算例计算局部坐标系下单元刚度矩阵（设E=1，长度以米为单位）6EI12 EIEl,EA,2EI4EIA,L;ILLL,L,L,L,柱60.50.046.9483.313.927.86.942.31梁1252.50.630.086.9413.927.83.470.58立柱：b,×h,=0.5m×1.0m横梁：b,×h,=0.5m×1.26m

（设E=1，长度以米为单位） i i L EI i i L EA i i L 2EI i i L 4EI 2 6 i i L EI 3 12 i i L EI Ai Ii Li 0.5 0.04 6 6.94 83.3 13.9 27.8 6.94 2.31 0.63 0.08 12 52.5 6.94 13.9 27.8 3.47 0.58 立柱：b1×h1=0.5m×1.0m 横梁：b2×h2=0.5m×1.26m 柱 梁 2.  算例 „ 计算局部坐标系下单元刚度矩阵

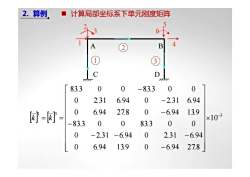
2. 算例■计算局部坐标系下单元刚度矩阵14BA②3cDMT777000083.3-83.3006.946.942.31-2.310013.96.9427.8- 6.94[] =[F =×10-3000083.383.300-6.942.31-2.31-6.94006.9413.9-6.9427.8

[ ] [ ] 3 1 3 10 0 6 94 139 0 6 94 278 0 2 31 6 94 0 2 31 6 94 833 0 0 833 0 0 0 6 94 278 0 6 94 139 0 2 31 6 94 0 2 31 6 94 833 0 0 833 0 0 − × ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡ − − − − − −− − = = . . . . . . . . . . . . . . . . . . . . k k 2 3 1 5 6 4 C D A B 1 2 3 2.  算例 „ 计算局部坐标系下单元刚度矩阵

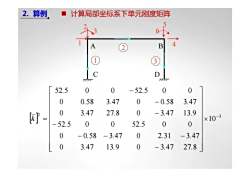
2. 算例■计算局部坐标系下单元刚度矩阵14BA2?LcDTTITT000052.5- 52.5003.473.470.58- 0.580013.927.83.47-3.47[K =×10-30 52.500052.500-3.472.31-3.47-0.580013.927.83.47-3.47

[ ] 3 2 10 0 3 47 13 9 0 3 47 27 8 0 0 58 3 47 0 2 31 3 47 52 5 0 0 52 5 0 0 0 3 47 27 8 0 3 47 13 9 0 0 58 3 47 0 0 58 3 47 52 5 0 0 52 5 0 0 − × ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡ − − − − − −− − = . . . . . . . . . . . . . . . . . . . . k 2.  算例 2 3 1 5 6 4 C D A B 1 2 3 „ 计算局部坐标系下单元刚度矩阵

2. 算例[k ] "（3）整体坐标系下单元刚度矩阵[ -["[[]00007°cosasina0000-sinacosa000010[7] =：.:.0000cosasina0000-sinacos a001]000

（3）整体坐标系下单元刚度矩阵 [ ] e k [ ] e sin a cos a cos a sin a sin a cos a cos a sin a T ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ − = 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 [ ] [ ] [ ] [ ] e eT e e k = T k T 2.  算例

2. 算例计算整体坐标系下单元刚度矩阵-i000001(α=900)单元1,300000-1000001[7] =...2BA000010200000-1130000L 01]DC1TTTT00-6.94-6.942.312.31/000083.383.3006.9413.96.9427.8[K] -[P =[][] [] 10-3002.316.942.316.94000083.3-83.30013.927.8]6.94[-6.94[T] = [][K2 = []单元2（α=00）A

[ ] e T ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ − = 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 [] [] [ ] [ ] [ ] 3 1 3 1 10 6 94 0 13 9 6 94 0 27 8 0 83 3 0 0 83 3 0 2 31 0 6 94 2 31 0 6 94 6 94 0 27 8 6 94 0 13 9 0 83 3 0 0 83 3 0 2 31 0 6 94 2 31 0 6 94 − × ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − − − = = = . . . . . . . . . . . . . . . . . . . . k k T k T T 2 3 1 5 6 4 C D A B 单元 1,3 （ α=90 0 ） 1 2 3 2.  算例 （ α=0 0 ） [T ] [] = I [ ] [ ] 2 2 单元 2 k = k „ 计算整体坐标系下单元刚度矩阵