《结构力学》课程授课教案（讲义）第九章 矩阵位移法 9.2 局部坐标系下的单元刚度矩阵

教学要求掌握局部坐标系下的单元刚度矩阵及其物理意义。9.2.1一般单元（1）杆端内力与位移关系回顾EANN=（轴向）：1Mas=418,+210g-6i号：Ma=210,+4i0-6i号（弯由);6(0+0)-6i元MAB+MBAOAB=1211（2）公式推导（图9-2）B-1刘212Z(e)1(e)(e).TyTa)坐标系b)位移分量c)力分量图9-2杆件性质：长度I，截面面积A，截面惯性矩I，弹性模量E；杆端位移u、V、e

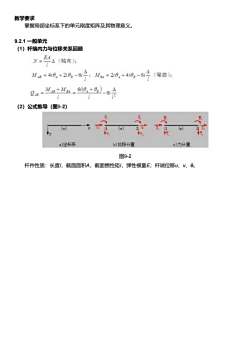
教学要求 掌握局部坐标系下的单元刚度矩阵及其物理意义。 9.2.1 一般单元 （1）杆端内力与位移关系回顾 （2）公式推导（图9-2） 图9-2 杆件性质：长度l，截面面积A，截面惯性矩I，弹性模量E；杆端位移u、v、θ

EA(ul(0)CX(0) --u2L(9.1)-(6)-50)X(0)(ur1E+2号0EIGMe+64-日五00-()MO-+6(vV1.-V2GEI(9.2)12EiO0-9)(6+60)+2336EI12EI(60)(e)+69-9-121列成矩阵形式：EAE.AX0000216EI12EI12EI6EI环五00卫12卫6EI6EI4EI2EIM百0012121(9.3)EAEAX,0000i1112EI6EI12EI6EI00中T222132EI6EI4EI6EI0百0M7731-国即：(9.4)局部坐标系下单元刚度矩阵)[EAEA00001112EI6EI6EI12EI073234EI6EI2EI0=1121(9.5)EA00112EI6EI对称234EI19.2.2简支梁简支梁单元见图9-3

9.2.2 简支梁 简支梁单元见图9-3

百商I花中#节双(e)(e)a)坐标系b)位移分量c)力分量图9-3说明：（a）梁单元通常忽略轴向变形：（b）图10-3中证==证，=V=0：相应的力分量也应该为零：（）依据刚度矩阵的物理意义，可以由一般单元的刚度矩阵生成梁单元矩阵。即去掉位移分量为零的相应行和列。EA福E*)RE16EI12EI6EI12EI行13313216E14EI6E12EI百M271E4EA0012EI6EI12年16EI子面2262EI6E1百M7211即：4EI2EI6.M1单元刚度方程：2EI4EIMJ611(9.6)4EI2E14212单元刚度矩阵：[=4EI[2141(9.7)9.2.3悬臂梁等思考：建立图9-4的单元刚度矩阵：（固定端位移为零；自由端有转角和竖向位移）卡一Y(e)(e)+ty6）悬臂梁a）一端固定，一端铰支

图9-3 9.2.3 悬臂梁等 思考：建立图9-4的单元刚度矩阵：（固定端位移为零；自由端有转角和竖向位移)

图9-412EI6EI412i五元SEI[=图a:[]=图b:007219.2.4桁架仅有轴向位移EAEAE1[=EA2工9.2.5单元刚度系数的意义一般地，第j个杆端位移分量取单位值1，其它杆端位移为0时所引起的第i个杆端力分量的值。6EI2(0)例的物理意义：当第3个杆端位移分量6=1时引起的第5个K5312杆端力分量。EAEAX0000116EI12EI12EI6EIT订0073P126EI4EI6EI2EIM.6.00711E.AEA0000X21712EI12EI6EI6EI00文V.12316EI6EI4EI2E100ME73221(1）对称性=（反力互等定理）（2）奇异性（不存在逆矩阵）根据式匠=可由杆端位移求解杆端力，且是唯一解。但由杆端力求杆端位移，可能无解，如有解也是非唯一解。说明：已知6个杆端力分量，（a）无法保证力状态的合法性一一可能造成无解；（b）无法确定杆的支承条件一一可能造成非唯一解

图9-4 9.2.4 桁架 仅有轴向位移 9.2.5 单元刚度系数的意义 一般地，第 j 个杆端位移分量取单位值1，其它杆端位移为 0 时所引起的第i个杆端力分量的值。 （1）对称性 （2）奇异性（不存在逆矩阵） 说明：已知6个杆端力分量，（a）无法保证力状态的合法性——可能造成无解；（b）无法确定 杆的支承条件——可能造成非唯一解