《结构力学》课程授课教案（讲义）第十章 结构动力计算 10-6 两自由度体系在简谐荷载下的强迫振动 Forced-Vibration of MDOF Due to Harmonic Loads

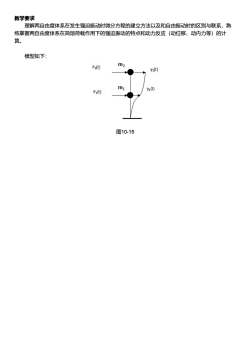
教学要求理解两自由度体系在发生强迫振动时微分方程的建立方法以及和自由振动时的区别与联系，熟练掌握两自由度体系在简谐荷载作用下的强迫振动的特点和动力反应（动位移、动内力等）的计算。模型如下：m2P2(t)yz(t)miYi(t)Pi(t)图10-15

教学要求 理解两自由度体系在发生强迫振动时微分方程的建立方法以及和自由振动时的区别与联系，熟 练掌握两自由度体系在简谐荷载作用下的强迫振动的特点和动力反应（动位移、动内力等）的计 算。 模型如下： 图10-15

控带方程（运动方程）mji(t)+k(t)+ka(t)=pi(t)mj (t)+kn(t)+kmy (t)=p, (t)设荷载为：Pi(t)=Pi sin et)P2(t)=P2 sin Ct则在平稳振动阶段，各质点也作简谐振动：Ji(t)-Yisina)y2(t)=Y2sinot代入运动方程得：(k1-gm)+=pk+(-m)=由此可得：D.-DY=D.D.其中：D,=(k1-m)(k-'m2)-kzk21D,=(k2-"m)Pi-k2P2D, =-kip +(k1-'m.)P由此可得y1(t)，y2(t)。我们可以看到当Do中的e与结构的任一自振频率相同时，则Do=0，当D1，D2不全为零时，位移幅值即为无限大，这时即出现共振现象。讲解例10.7对多自由度体系的情况同样可得

由此可得y1(t)，y2(t)。 我们可以看到当D0中的θ与结构的任一自振频率相同时，则D0=0，当D1，D2不全为零时，位移 幅值即为无限大，这时即出现共振现象。 讲解例10.7 对多自由度体系的情况同样可得