《建筑结构抗震》课程授课教案(讲义)第三章 结构地震反应分析与抗震验算 3.6 竖向地震作用 3.7 结构平扭耦合地震反应与双向水平地震影响

教案及讲义建筑结构抗震第七讲河北联合大学建筑工程学院
教案及讲义 建筑结构抗震 第七讲 河北联合大学建筑工程学院
教案8课程名称《建筑结构抗震》授课专业土木工程授课内容第三章结构地震反应分析与抗震验算3.6竖向地震作用3.7结构平扭耦合地震反应与双向水平地震影响知识熟悉了解竖向地震作用计算方法;教目标学能力①熟练掌握竖向地震作用计算方法:②了解结构平扭耦合地震反应与双向水平I目标地震影响标德育培养执著追求科学的精神,并不断提出多种解决问题的思路目标教重点①竖向地震作用计算方法材难点结构平扭耦合地震反应分析关键计算竖向地震作用教学设备传统板书教教法公式推导带领学生演算练习学方学法紧扣概念→强调计算→总结→思考法教学环节教学内容教师调控学生活动时间组织教学2'师生问好5'导入新课教师提问,学生思考,以复习前一章知识导入本次课内容。1、复习多质点弹性体系水平地震作用;2、讲述竖向地震作用计算方法;教师边讲边启发边归纳边强新授82'3、讲述结构平扭耦合地震反应与双向水调。提出问题,让学生回答,平地震影响之后给出正确答案。4、总结该节课的教学内容。3'课堂练习分别让学生回答。给出思考题、判断题1、归纳竖向地震作用的计算公式,3'课后小结学生总结→教师归纳补充计算题作业做到作业本上作业5'教研室主任签字通过课件教学,调动了学生学习的积极性,掌握了相关的课堂评价基本知识,做到结合规范教学,达到了教学目标要求,教学效果较好
课程名称 《建筑结构抗震》 授课专业 土木工程 授课内容 第三章 结构地震反应分析与抗震验算 3.6 竖向地震作用 3.7 结构平 扭耦合地震反应与双向水平地震影响 教 学 目 标 知识 目标 熟悉了解竖向地震作用计算方法; 能力 目标 ① 熟练掌握竖向地震作用计算方法;② 了解结构平扭耦合地震反应与双向水平 地震影响 德育 目标 培养执著追求科学的精神,并不断提出多种解决问题的思路 教 材 分 析 重点 ①竖向地震作用计算方法 难点 结构平扭耦合地震反应 关键 计算竖向地震作用 教学设备 传统板书 教 学 方 法 教法 公式推导 带领学生演算练习 学法 紧扣概念→强调计算→总结→思考 教学环节 教学内容 教师调控学生活动 时间 组织教学 师生问好 2` 导入新课 1、以复习前一章知识导入本次课内容。 教师提问,学生思考, 5’ 新授 1、复习多质点弹性体系水平地震作用; 2、讲述竖向地震作用计算方法; 3、讲述结构平扭耦合地震反应与双向水 平地震影响 4、总结该节课的教学内容。 教师边讲边启发边归纳边强 调。提出问题,让学生回答, 之后给出正确答案。 82’ 课堂练习 给出思考题、判断题 分别让学生回答。 3’ 课后小结 1、 归纳竖向地震作用的计算公式, 学生总结→教师归纳 3’ 作业 补充计算题 作业做到作业本上 5` 课堂评价 通过课件教学,调动了学生学习的积极性,掌握了相关的 基本知识,做到结合规范教学,达到了教学目标要求,教 学效果较好。 教研室主任签字 教案 8

讲义83.6竖向地震作用震害调查表明,在烈度较高的震中区,竖向地震对结构的破坏也会有较大影响。烟肉等高算结构和高层建筑的上部在竖向地震的作用下,因上下振动,而会出现受拉破坏,对于大跨度结构,竖向地震引起的结构上下振动惯性力,相当增加结构的上下荷载作用。因此我国抗震规范(GB50011一2001)规定:设防烈度为8度和9度区的大跨度屋盖结构,长悬臂结构,烟及类似高笃结构和设防烈度为9度区的高层建筑,应考虑竖向地震作用。3.6.1高耸结构及高层建筑可采用类似于水平地震作用的底部剪力法,计算高结构及高层建筑的竖向地震作用。即先确定结构底部总竖向地震作用,再计算作用在结构各质点上的竖向地震作用(参见图3-24),公式为FEVk=αviGeg(3-157)G,Hi-FEVKFv=(3-158)ZG,H)j=IFm+ GrFn+GiHFEI图3-24高算结构与高层建筑竖向地震作用式中FEV一结构总竖向地震作用标准值FV一质点I的竖向地震作用标准值:αvl一按结构竖向基本周期计算的竖向地震影响系数;Ge一结构等效总重力荷载。上式中结构等效总重力荷载同样按式(3-128)计算,其中等效系数%可按式(3-132)确定。由于高算结构或高层建筑质点数n较大,规范规定统一取%=0.75,即计算高算结构或高层建筑竖向地震作用时,结构等效总重力荷载取为实际总重力荷载的75%。分析表明,竖向地震反应谱与水平地震反应谱大致相同,因此竖向地震影响系数谱与图3-12所示水平地震影响系数谱形状类似。因高耸结构或高层建筑竖向基本周期很短,一般处在地震影响系数最大值的周期范围内,同时注意到竖向地震动加速度峰值为水平地震动加
讲义 8 3.6 竖向地震作用 震害调查表明,在烈度较高的震中区,竖向地震对结构的破坏也会有较大影响。烟囱等 高耸结构和高层建筑的上部在竖向地震的作用下,因上下振动,而会出现受拉破坏,对于大 跨度结构,竖向地震引起的结构上下振动惯性力,相当增加结构的上下荷载作用。因此我国 抗震规范(GB50011—2001)规定:设防烈度为 8 度和 9 度区的大跨度屋盖结构,长悬臂结 构,烟囱及类似高耸结构和设防烈度为 9 度区的高层建筑,应考虑竖向地震作用。 3.6.1 高耸结构及高层建筑 可采用类似于水平地震作用的底部剪力法,计算高耸结构及高层建筑的竖向地震作用。 即先确定结构底部总竖向地震作用,再计算作用在结构各质点上的竖向地震作用(参见图 3-24),公式为 FEVk =V1Geg (3-157) EVk n j j j i i Vi F G H G H F = = 1 2 (3-158) Hi FEVk FVn FVi Gi Gn 图 3-24 高耸结构与高层建筑竖向地震作用 式中 FEVk —结构总竖向地震作用标准值; FVi —质点 I 的竖向地震作用标准值; V1—按结构竖向基本周期计算的竖向地震影响系数; Geg —结构等效总重力荷载。 上式中结构等效总重力荷载同样按式(3-128)计算,其中等效系数 可按式(3-132) 确定。由于高耸结构或高层建筑质点数 n 较大,规范规定统一取 =0.75,即计算高耸结构 或高层建筑竖向地震作用时,结构等效总重力荷载取为实际总重力荷载的 75%。 分析表明,竖向地震反应谱与水平地震反应谱大致相同,因此竖向地震影响系数谱与图 3-12 所示水平地震影响系数谱形状类似。因高耸结构或高层建筑竖向基本周期很短,一般 处在地震影响系数最大值的周期范围内,同时注意到竖向地震动加速度峰值为水平地震动加
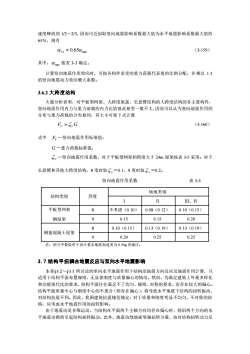
速度峰值的1/2~2/3,因而可近似取竖向地震影响系数最大值为水平地震影响系数最大值的65%,则有(3-159)αv=0.65αmx其中,αmx按表3-3确定。计算竖向地震作用效应时,可按各构件承受的重力荷载代表值的比例分配,并乘以1.5的竖向地震动力效应增大系数。3.6.2大跨度结构大量分析表明,对平板型网架、大跨度屋盖、长悬臂结构的大跨度结构的各主要构件,竖向地震作用内力与重力荷载的内力比值彼此相差一般不大,因而可以认为竖向地震作用的分布与重力荷载的分布相同,其大小可按下式计算F=SrG(3-160)式中F一竖向地震作用标准值;G一重力荷载标准值:5v一竖向地震作用系数,对于平板型网架和跨度大于24m屋架按表3-5采用;对于长悬臂和其他大跨度结构,8度时取,=0.1,9度时取=0.2。表3-5竖向地震作用系数场地类别烈度结构类别II1III、IV8平板型网架不考虑(0.10)0.08(0.12)0.10(0.15)90.150.150.20钢屋架80.10(0.15)0.13(0.19)0.13(0.19)钢筋混凝土屋架90.200.250.25注:括号中数值用于设计基本地震加速度为0.30g的地区。3.7结构平扭合地感反应与双向水平地震彩响本章83.2~83.5所讨论的单向水平地震作用下结构沿地震方向反应及地震作用计算,只适用于结构平面布置规则、无显著刚度与质量偏心的情况。然而,为满足建筑上外观多样化和功能现代化的要求,结构平面往往满足不了均匀、规则、对称的要求,而存在较大的偏心。结构平面质量中心与刚度中心的不重合(即存在偏心),将导致水平地震下结构的扭转振动,对结构抗震不利。因此,我国建筑抗震规范规定:对于质量和刚度明显不均匀、不对称的结构,应考虑水平地震作用的扭转影响。由于地震动是多维运动,当结构在平面两个主轴方向均存在偏心时,则沿两个方向的水平地震动都将引起结构扭转振动。此外,地震动绕地面竖轴扭转分量,也对结构扭转动力反
速度峰值的 1/2~2/3,因而可近似取竖向地震影响系数最大值为水平地震影响系数最大值的 65%,则有 1 65 max V = 0. (3-159) 其中, max 按表 3-3 确定。 计算竖向地震作用效应时,可按各构件承受的重力荷载代表值的比例分配,并乘以 1.5 的竖向地震动力效应增大系数。 3.6.2 大跨度结构 大量分析表明,对平板型网架、大跨度屋盖、长悬臂结构的大跨度结构的各主要构件, 竖向地震作用内力与重力荷载的内力比值彼此相差一般不大,因而可以认为竖向地震作用的 分布与重力荷载的分布相同,其大小可按下式计算 FV = VG (3-160) 式中 FV —竖向地震作用标准值; G —重力荷载标准值; V —竖向地震作用系数,对于平板型网架和跨度大于 24m 屋架按表 3-5 采用;对于 长悬臂和其他大跨度结构,8 度时取 v =0.1,9 度时取 v =0.2。 竖向地震作用系数 表 3-5 结构类别 烈度 场地类别 Ⅰ Ⅱ Ⅲ、Ⅳ 平板型网架 钢屋架 8 不考虑(0.10) 0.08(0.12) 0.10(0.15) 9 0.15 0.15 0.20 钢筋混凝土屋架 8 0.10(0.15) 0.13(0.19) 0.13(0.19) 9 0.20 0.25 0.25 注:括号中数值用于设计基本地震加速度为 0.30g 的地区。 3.7 结构平扭耦合地震反应与双向水平地震影响 本章§3.2~§3.5 所讨论的单向水平地震作用下结构沿地震方向反应及地震作用计算,只 适用于结构平面布置规则、无显著刚度与质量偏心的情况。然而,为满足建筑上外观多样化 和功能现代化的要求,结构平面往往满足不了均匀、规则、对称的要求,而存在较大的偏心。 结构平面质量中心与刚度中心的不重合(即存在偏心),将导致水平地震下结构的扭转振动, 对结构抗震不利。因此,我国建筑抗震规范规定:对于质量和刚度明显不均匀、不对称的结 构,应考虑水平地震作用的扭转影响。 由于地震动是多维运动,当结构在平面两个主轴方向均存在偏心时,则沿两个方向的水 平地震动都将引起结构扭转振动。此外,地震动绕地面竖轴扭转分量,也对结构扭转动力反

应有影响,但由于目前缺乏地震动扭转分量的强震记录,因而由该原因引起的扭转效应还难于确定。下面主要讨论由水平地震引起的多高层建筑结构平扭耦合地震反应。3.7.1平扭耦合体系的运动方程根据多高层建筑的特点,为简化计算,可采用以下假定:(1)建筑各层楼板在其自身平面内为绝对刚性,楼板在其水平面内的移动为刚体位移。(2)建筑整体结构由多榻平面内受力的抗侧力结构(框架或剪力墙)构成,如图3-25所示。各抗侧力结构在其自身平面内刚度很大,在平面外刚度较小,可以忽略。(3)结构的抗扭刚度主要由各榻抗侧力结构的侧移恢复力提供,结构所有构件自身的抗扭作用可以忽略。(4):将所有质量(包括梁、柱、墙等质量)都集中到各层楼板处。vInu图3-25平面抗侧力结构与楼板坐标系在上述假定下,结构的运动可用每一楼层某一参考点沿两个正交方向的水平移动和绕通过该点竖轴的转动来描述。为便于结构运动方程的建立,可将各楼层的质心定为楼层运动参考点。这样,描述结构各楼层运动的楼层坐标系原点不一定同一竖轴上(如图3-26所示),但各楼层坐标轴方向一致。y/0.1yAxyAxO,yAT万图3-26结构整体坐标系利用达朗贝尔原理,按结构静力分析的矩阵位移方法,可建立多高层建筑在双向水平地
应有影响,但由于目前缺乏地震动扭转分量的强震记录,因而由该原因引起的扭转效应还难 于确定。下面主要讨论由水平地震引起的多高层建筑结构平扭耦合地震反应。 3.7.1 平扭耦合体系的运动方程 根据多高层建筑的特点,为简化计算,可采用以下假定: (1) 建筑各层楼板在其自身平面内为绝对刚性,楼板在其水平面内的移动为刚体位移。 (2) 建筑整体结构由多榀平面内受力的抗侧力结构(框架或剪力墙)构成,如图 3-25 所 示。各榀抗侧力结构在其自身平面内刚度很大,在平面外刚度较小,可以忽略。 (3) 结构的抗扭刚度主要由各榀抗侧力结构的侧移恢复力提供,结构所有构件自身的抗 扭作用可以忽略。 (4) 将所有质量(包括梁、柱、墙等质量)都集中到各层楼板处。 ok y bik aik o v φik u 图 3-25 平面抗侧力结构与楼板坐标系 在上述假定下,结构的运动可用每一楼层某一参考点沿两个正交方向的水平移动和绕通 过该点竖轴的转动来描述。为便于结构运动方程的建立,可将各楼层的质心定为楼层运动参 考点。这样,描述结构各楼层运动的楼层坐标系原点不一定同一竖轴上(如图 3-26 所示), 但各楼层坐标轴方向一致。 图 3-26 结构整体坐标系 利用达朗贝尔原理,按结构静力分析的矩阵位移方法,可建立多高层建筑在双向水平地

震作用下的运动方程为(3-161)[K](D} ={F)+{F)式中[(D.)](D) =3(D,))(3-162)[(D,](D}、(D,)一结构各楼层质心沿x轴平移和沿y轴平移向量;(D。一结构各楼层扭转角向量;[K]一结构总体刚度矩阵;[K]-Z[K];(3-163)[K],一第i榻抗侧力结构在整体坐标系下的刚度矩阵;[Kxx] [K,] [Kx ](3-164)[K], =[K,x] [Ky] [Kyo ];[Kax ][Ky] [Kop ]][K, ] = cos? ,[K, ] [K, ]i =[K x] = cosO, sin 0,[Ku]][K, ] = sin ,[K, ][K xp ]; =[K ax ] = cos;(- cos0,[b]; + sin 0,[a], [Ku ]i[K ve ]; =[K] = sin e,(- coso,[b], + sin @,[a],)[K, ][K., ] =(-cosの,[b], + sin 9,[a],)"[K, ][ailai2[a]; =(3-166a)ain]
震作用下的运动方程为 I [ ]{ } { } { } K D F F = + c (3-161) 式中 = { } { } { } { } D D D D y x (3-162) { } Dx 、{ } Dy —结构各楼层质心沿 x 轴平移和沿 y 轴平移向量; { } D —结构各楼层扭转角向量; [K]—结构总体刚度矩阵; K = K i [ ] [ ] (3-163) K i [ ] —第 i 榀抗侧力结构在整体坐标系下的刚度矩阵; = i i i i i i i i i [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] K K K K K K K K K K x y yx yy y xx xy x i (3-164) Kxx i Ku i [ ] cos [ ] 2 i = i i u i T [Kxy ] [K yx ]i cos sin [K ] i = = Kyy i Ku i [ ] sin [ ] 2 i = i i i i i u i T [Kx ] [K x ]i cos ( cos [b] sin [a] )[K ] i = = − + i i i i i u i T [K y ] [K y ]i sin ( cos [b] sin [a] )[K ] i = = − + K i b i i a i Ku i [ ] ( cos [ ] sin [ ] ) [ ] 2 i = − + = in i i i a a a a 2 1 [ ] (3-166a)

[bibi2[6b]; =(3-166b)bin[K,]一第i榻抗侧力结构在其自身平面内的楼层侧移刚度矩阵;αij、b,一第i榻抗侧力结构上任一固定点在结构第j层整体坐标下的坐标值(参见图3-25);9,一第i榻抗侧力与整体坐标x轴间夹角;[(Fx)](F1)=3(Fly)(3-167)[(Fio]](Fix}、(Fry)一作用在结构各楼层质心处沿x轴和沿y轴水平惯性力向量;(F1}一作用在结构各楼层惯性扭矩向量;(Fix} = -([MI(Dx)+[M](1) xg)(Fry} = -([M](D,)+[M](I) yg)(3-168)(Fro) =-{J(D.)x、y一沿x轴和y轴方向水平地面运动加速度;[m,m,[m] =(3-169)m
= in i i i b b b b 2 1 [ ] (3-166b) Ku i [ ] —第 i 榀抗侧力结构在其自身平面内的楼层侧移刚度矩阵; ij a 、 ij b —第 i 榀抗侧力结构上任一固定点在结构第 j 层整体坐标下的坐标值(参见 图 3-25); i —第 i 榀抗侧力与整体坐标 x 轴间夹角; = { } { } { } I IY IX I F F F F (3-167) { } FIX 、{ } FIY —作用在结构各楼层质心处沿 x 轴和沿 y 轴水平惯性力向量; { } FI —作用在结构各楼层惯性扭矩向量; { } ([ ]{ } [ ]{1} ) •• •• IX = − x + g F M D M x { } ([ ]{ } [ ]{1} ) •• •• IY = − y + g F M D M y (3-168) { } [ ]{ } •• = − D F J I •• g x 、 •• g y —沿 x 轴和 y 轴方向水平地面运动加速度; = mn m m m 2 1 [ ] (3-169)

[J1J[]]=(3-170)Jnm,一结构第i楼层的质量;J一结构第i楼层绕本层质心的转动惯量:n一结构的楼层数;(F)一阻尼力向量。由式(3-167)、(3-168),(F)可表示为(F) = -([M)(D)+[M)(D,)(3-171)式中【M]一结构总质量矩阵;[m][M]=[m](3-172)[].1Xg.(Dg)=myg(3-173)<(0)(1)、(0一分别为由n个1元素和n个0元素组成的向量。由粘滞阻尼理论,结构阻尼力向量可表达为(F} = -[CI(D)(3-174)式中[C]一结构总体阻尼矩阵,可采用瑞雷阻尼模型通过结构总体刚度矩阵和总体质量矩阵线性组合获得。将式(3-171)、(3-174)代入式(3-161),得结构平扭耦合运动微分方程为[MI(D) +[CI(D) +[K](D) = -[M](D,)(3-175)3.7.2平扭耦合体系的地震作用由体系的自由振动方程
= n J J J J 2 1 [ ] (3-170) mi —结构第 i 楼层的质量; i J —结构第 i 楼层绕本层质心的转动惯量; n—结构的楼层数; { } Fc —阻尼力向量。 由式(3-167)、(3-168), { } FI 可表示为 { } ([ ]{ } [ ]{ }) •• •• FI = − M D + M Dg (3-171) 式中 [M ]—结构总质量矩阵; = [ ] [ ] [ ] [ ] J m m M (3-172) = •• •• •• {0} {1} {1} { } g g g y x D (3-173) {1}、{0}—分别为由 n 个 1 元素和 n 个 0 元素组成的向量。 由粘滞阻尼理论,结构阻尼力向量可表达为 { } [ ]{ } • Fc = − C D (3-174) 式中 [C]—结构总体阻尼矩阵,可采用瑞雷阻尼模型通过结构总体刚度矩阵和总体质量矩 阵线性组合获得。 将式(3-171)、(3-174)代入式(3-161),得结构平扭耦合运动微分方程为 [ ]{ } [ ]{ } [ ]{ } [ ]{ } •• • •• M D + C D + K D = − M Dg (3-175) 3.7.2 平扭耦合体系的地震作用 由体系的自由振动方程

(3-176)[M](D) +[K](D) = -(0)可求得体系的各阶周期为T,振型为[(x,]](3-177)(0,)=30,j =1,2,..",3n,[(0,]]其中(x)=[x1,x2",x,]"(,) =[yny2,ym](3-178)(0,}=[βP2,Pm]式中xi、y一振型j楼层i质心沿x轴和y轴方向的水平位移;βn一振型j楼层i的扭转角。令(D) =Zq,(0,)(3-179)将式(3-179)代入运动方程(3-175),利用振型的正交性,按与式(3-97)相同的推导方法,可得正则坐标q,的控制方程为(3-180)qj+20j5jgj+0j=-gXg-ryyg式中x、y一分别为x方向地震动和y方向地震动振型参与系数,20i=1(3-181a)Yxj=1E(x)+rG+1yii=12yc,i=1(3-181b)Yy=P7之(+++rp)Gi=lG,=m,gr=m;由于地震反应谱是关于一个地震记录定义的,因此,如果采用振型分解反应谱法求平扭耦合体系最大反应,则只能考虑单向水平地震动的影响,此时体系水平地震作用的计算公式
[ ]{ }+[ ]{ } = −{0} •• M D K D (3-176) 可求得体系的各阶周期为 Tj,振型为 = { } { } { } { } j j j j y x j = 1,2, ,3n , (3-177) 其中 T j j j jn {x } [x , x , , x ] 1 2 = T j j j jn {y } [y , y , , y ] 1 2 = (3-178) T j j j jn { } [ , , , ] = 1 2 式中 ji x 、 ji y —振型 j 楼层 i 质心沿 x 轴和 y 轴方向的水平位移; ji —振型 j 楼层 i 的扭转角。 令 { } = { } D qj j (3-179) 将式(3-179)代入运动方程(3-175),利用振型的正交性,按与式(3-97)相同的推导 方法,可得正则坐标 j q 的控制方程为 •• • •• •• j + j j j + j = − xj g − yj g q g x y 2 2 (3-180) 式中 xj 、 yj —分别为 x 方向地震动和 y 方向地震动振型参与系数, = = + + = n i ji ji i ji i n i ji i xj x y r G x G 1 2 2 2 2 1 ( ) (3-181a) = = + + = n i ji ji i ji i n i ji i yj x y r G y G 1 2 2 2 2 1 ( ) (3-181b) Gi = mi g i i i m J r = 由于地震反应谱是关于一个地震记录定义的,因此,如果采用振型分解反应谱法求平扭 耦合体系最大反应,则只能考虑单向水平地震动的影响,此时体系水平地震作用的计算公式

为Fxi=G,αjYuXji(3-182)Fyi=GajYyyjFoji=G,αjYyrpj式中Fx、Fji一分别为振型j楼层i质心处x方向和y方向水平地震作用标准值;Fai一振型j楼层i扭转地震作用标准值;Y,一振型参与系数,当仅考虑x方向地震动时,Y=:当仅考虑y方向地震动时=:当考虑与x方向斜交角的地震时,=cos+Sin;α,一与体系自振周期T相应的地震影响系数。3.7.3振型组合由每一振型地震作用按静力分析方法求得某一特定最大振型地震反应后,同样需进行振型组合求该特定最大总地震反应。与结构单向平移水平地震反应计算相比,考虑平扭耦合效应进行振型组合时,需注意由于平扭耦合体系有x向、y向和扭转三个主振方向,取3r个振型组合可能只相当于不考虑平扭耦合影响时只取r个振型组合的情况,故平扭耦合体系的组合数比非平扭耦合体系的振型组合数多,一般应为3倍以上。此外,由于平扭耦合影响,一些振型的频率间隔可能很小,振型组合时,需考虑不同振型地震反应间的相关性。为此,可采用完全二次振型组合法(CQC法),即按下式计算地震作用效应SrrS=.EEpis,Sk(3-183)Vj= k=l其中8(1+)52(3-184)P次=(1-次)2+2(1+)(1+)52式中S,、S一分别为振型和振型k地震作用效应:Pjk一振型j和振型k相关系数,式(3-184)是按各阶振型阻尼比均相等时得出的;f一振型k与振型j的自振周期比;5一结构阻尼比;r一振型组合数,可取r=9~15。表3-6列出了P与的关系(取=0.05),从中可以看出,P随两个振型周期比
为 xji i j tj ji F = G x yji i j tj ji F = G y (3-182) ji i j tj i ji F G r 2 = 式中 Fxji 、 Fyji —分别为振型 j 楼层 i 质心处 x 方向和 y 方向水平地震作用标准值; Fji —振型 j 楼层 i 扭转地震作用标准值; tj —振型参与系数,当仅考虑 x 方向地震动时, tj xj = ;当仅考虑 y 方向地震动 时 tj yj = ;当考虑与 x 方向斜交θ角的地震时, tj = xj cos + yj sin ; j —与体系自振周期 Tj 相应的地震影响系数。 3.7.3 振型组合 由每一振型地震作用按静力分析方法求得某一特定最大振型地震反应后,同样需进行振 型组合求该特定最大总地震反应。与结构单向平移水平地震反应计算相比,考虑平扭耦合效 应进行振型组合时,需注意由于平扭耦合体系有 x 向、y 向和扭转三个主振方向,取 3r 个 振型组合可能只相当于不考虑平扭耦合影响时只取 r 个振型组合的情况,故平扭耦合体系的 组合数比非平扭耦合体系的振型组合数多,一般应为 3 倍以上。此外,由于平扭耦合影响, 一些振型的频率间隔可能很小,振型组合时,需考虑不同振型地震反应间的相关性。为此, 可采用完全二次振型组合法(CQC 法),即按下式计算地震作用效应 S = = = r j r k S jk S j Sk 1 1 (3-183) 其中 2 2 2 2 2 1.5 2 (1 ) 2(1 ) (1 ) 8(1 ) T T T T T jk − + + + + = (3-184) 式中 j S 、 k S —分别为振型 j 和振型 k 地震作用效应; jk —振型 j 和振型 k 相关系数,式(3-184)是按各阶振型阻尼比均相等时得出的; T —振型 k 与振型 j 的自振周期比; —结构阻尼比; r —振型组合数,可取 r =9~15。 表 3-6 列出了 jk 与 T 的关系(取 =0.05),从中可以看出, jk 随两个振型周期比 T
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《建筑结构抗震》课程授课教案(讲义)第三章 结构地震反应分析与抗震验算 3.8 结构非弹性地震反应分析.doc
- 《建筑结构抗震》课程授课教案(讲义)第四章 多层砌体结构抗震设计 4.2砌体结构的抗震计算4.3砌体结构抗震构造措施.doc
- 《建筑结构抗震》课程授课教案(讲义)第三章 结构地震反应分析与抗震验算 3.9 结构抗震验算.doc
- 《建筑结构抗震》课程授课教案(讲义)第四章 多层砌体结构抗震设计 4.1砌体结构震害特点4.2多层砌体结构选型与布置.doc
- 《建筑结构抗震》课程授课教案(讲义)第六章 隔震、减震与结构控制初步.doc
- 《建筑结构抗震》课程授课教案(讲义)第五章 多层及高层钢筋混凝土房屋抗震设计5.1多高层建筑钢筋混凝土结构的震害及其分析 5.2 选型、结构布置和设计原则.doc
- 《建筑结构抗震》课程授课教案(讲义)第五章 多层及高层钢筋混凝土房屋抗震设计 5.4 抗震墙结构的抗震设计 5.5 框架-抗震墙结构的抗震设计.doc
- 《建筑结构抗震》课程授课教案(讲义)第五章多层及高层钢筋混凝土房屋抗震设计5.3钢筋混凝土框架结构的抗震设计.doc
- 《建筑结构抗震》课程教学大纲 Seismic Design of Building Structures.doc
- 上海交通大学:船舶海洋与建筑工程学院土木工程专业课程教学大纲汇编(合集一,共五十八门).pdf
- 《桥梁工程》课程教学课件(专题讲稿)桥梁设计讲座.pdf
- 《桥梁工程》课程教学课件(专题讲稿)Principles for Concept Design of Conrete Girder Bridges.pdf
- 《桥梁工程》课程学习指南.pdf
- 《桥梁工程》课程教学大纲 Bridge Engineering.pdf
- 《结构力学》课程授课教案(讲义)第十章 结构动力计算 10-7 小结.pdf
- 《结构力学》课程授课教案(讲义)第十章 结构动力计算 10-6 两自由度体系在简谐荷载下的强迫振动 Forced-Vibration of MDOF Due to Harmonic Loads.pdf
- 《结构力学》课程授课教案(讲义)第十章 结构动力计算 10-5 两个自由度体系的自由振动 Free-Vibration of MDOF.pdf
- 《结构力学》课程授课教案(讲义)第十章 结构动力计算 10-4 阻尼对振动的影响 Influence of damping.pdf
- 《结构力学》课程授课教案(讲义)第十章 结构动力计算 10-3 单自由度体系的强迫振动 SDOF forced-Vibration.pdf
- 《结构力学》课程授课教案(讲义)第十章 结构动力计算 10-2 单自由度体系的自由振动 SDOF-Free Vibration.pdf
- 《建筑结构抗震》课程授课教案(讲义)第三章 结构地震反应分析与抗震验算 3.5 多质点弹性体系的水平地震作用.doc
- 《建筑结构抗震》课程授课教案(讲义)第三章 结构地震反应分析与抗震验算 3.4 多自由度弹性体系的地震反应分析 3.5 多质点弹性体系的水平地震作用.doc
- 《建筑结构抗震》课程授课教案(讲义)第三章 结构地震反应分析与抗震验算 3.1 概述 3.2 单自由度体系的弹性地震反应分析 3.3 单自由度弹性体系的水平地震作用及其反应谱.doc
- 《建筑结构抗震》课程授课教案(讲义)实验指导书及实验报告.doc
- 《建筑结构抗震》课程授课教案(讲义)第一章 绪论 1.4 工程抗震设防 1.5 抗震设计的总体要求.doc
- 《建筑结构抗震》课程授课教案(讲义)第二章 场地地基和基础 2.3 地基土液化及其防治.doc
- 《建筑结构抗震》课程授课教案(讲义)第二章 场地地基和基础 2.1 场地划分与场地区划 2.2 地基抗震验算.doc
- 《建筑结构抗震》课程授课教案(讲义)第一章 绪论 1.1 地震 1.2 地震震级和烈度 1.3 地震震害概述.doc
- 《建筑结构抗震》课程教学资源(试卷习题)习题及参考答案.doc
- 《建筑结构抗震》课程教学资源(试卷习题)抗震试卷1(试题).doc
- 《建筑结构抗震》课程教学资源(试卷习题)抗震试卷2(试题).doc
- 《建筑结构抗震》课程教学资源(试卷习题)抗震试卷1(答案).doc
- 《建筑结构抗震》课程教学资源(试卷习题)抗震试卷2(答案).doc
- 《建筑结构抗震》课程教学资源(PPT课件)第五章 多高层建筑钢筋混凝土结构抗震设计 5.1 多高层钢筋混凝土结构的震害及其分析 5.2 选型、结构布置和设计原则.ppt
- 《建筑结构抗震》课程教学资源(PPT课件)第五章 多高层建筑钢筋混凝土结构抗震设计 5.3 钢筋混凝土框架结构的抗震设计.ppt
- 《建筑结构抗震》课程教学资源(PPT课件)第五章 多高层建筑钢筋混凝土结构抗震设计 5.4 抗震墙结构的抗震设计 5.5 框架抗震墙结构的抗震设计.ppt
- 《建筑结构抗震》课程教学资源(PPT课件)第六章:隔震减震与结构控制初步.ppt
- 《建筑结构抗震》课程教学资源(PPT课件)第三章 结构地震反应分析与抗震计算 3.9 结构抗震验算.ppt
- 《建筑结构抗震》课程教学资源(PPT课件)第四章 多层砌体结构抗震设计 §4.1 多层砌体结构的震害特点 §4.2 多层砌体结构选型与布置.ppt
- 《建筑结构抗震》课程教学资源(PPT课件)第四章 多层砌体结构抗震设计 §4.3 多层砌体结构的抗震计算 §4.4 多层砌体结构抗震构造措施.ppt
