内蒙古科技大学：《材料力学》课程授课教案（讲义）第35讲 静不定系统（Ⅰ）

材料力学教案第35讲教学方案一静不定系统（1）基本内1.静不定系统。容2.力法。教学1.静不定结构系统的基本概念目2.掌握桁架、刚架静不定次数的判定。的3.掌握力法的基本原理及计算公式的导出。4.正则方程式与正则方程组的建立。1：重点掌握静不定结构系统的静不定次数的确定。重点2重点掌握正则方程式与正则方程组的建立、主系数、副系数、登自由项的计算方法。点3．难点是正确确定多次静不定系统的静不定次数及正确地解正则方程组。本次教学计划学时：2学时。教课堂讨论：学安

材 料 力 学 教 案 第 35 讲 教学方案 —— 静不定系统（Ⅰ） 基 本 内 容 1. 静不定系统。 2. 力法。 教 学 目 的 1. 静不定结构系统的基本概念。 2. 掌握桁架、刚架静不定次数的判定。 3. 掌握力法的基本原理及计算公式的导出。 4. 正则方程式与正则方程组的建立。 重 点 、 难 点 1. 重点掌握静不定结构系统的静不定次数的确定 。 2. 重点掌握正则方程式与正则方程组的建立、主系数、副系数、 自由项的计算方法。 3. 难点是正确确定多次静不定系统的静不定次数及正确地解 正则方程组。 教 学 安 排 本次教学计划学时：2 学时。 课堂讨论：

第+1.刚架系统与桁架系统的超静定次数的确定。2.力法的基本原理是什么？与变形比较法有何区别？3.用什么方法计算主系数、副系数、自由项最方便？4.如何正确应用图乘法？

第 三 十 五 讲 1. 刚架系统与桁架系统的超静定次数的确定。 2. 力法的基本原理是什么？与变形比较法有何区别？ 3. 用什么方法计算主系数、副系数、自由项最方便？ 4．如何正确应用图乘法？

材料力学教第十四章静不定问题分析$14-1静不定结构概述1.定义用静力学平衡方程无法确定全部约束力和内力的结构或结构系统，统称为静不定结构或系统，也称为超静定构或系统。X(b)(b)公AA金A图12-1静定结构与儿何可变系图12-2静不定结构2.静定、静不定结构（系统）无多余联系的几何不变的承载结构系统，其全部支承反力与内力都可由静力平衡条件求得，此系统称为静定结构或系统。静定结构除了变形外，没有可运动的自由度（图12-1（ab）如解除简支梁的右端铰支座，或解除悬臂梁固端对转动约束，使之成为铰支座，则此时的梁变成了图12.1（c）的可动机构，是几何可变系不能承受横向载荷。在无多余联系的几何不变的静定系统上增加约束或联系，称为多余约束，并因而产生多余约束反力，则这样的有多余约束的系统，仅利用静力平衡条件无法求得其反力和内力，称为静不定（或超静定）系统，如图12-2。外静不定：静不定结构的外部支座反力不能全由静力平衡方程求出的情况，常称为外静不定结构（图12-2b，d）内静不定：静不定结构内部约束（或联系)形成的内力不能单由静力平衡方程求出的情况称为内静不定结构（图12-2a，c）对于内、外静不定兼而有之的结构，有时称为混合静不定结构。3.静不定次数的确定1）根据结构药束性质可确定内、外约束力总数，内、外约束力总数与独立静力平衡方程总数之差即为静不定结构的静不定次数。2）外静不定的判断：根据结构与受力性质，确定其是空间或是平面承载结构，即可确定全部约束的个数。根据作用力的类型，可确定独立平衡方程数，二者之差为静不定次数

材 料 力 学 教 案 第十四章 静不定问题分析 §14-1 静不定结构概述 1．定义 用静力学平衡方程无法确定全部约束力和内力的结构或结构系统，统称为静不定结构或 系统，也称为超静定结构或系统。 2．静定、静不定结构（系统） 无多余联系的几何不变的承载结构系统，其全部支承反力与内力都可由静力平衡条件求 得，此系统称为静定结构或系统。静定结构除了变形外，没有可运动的自由度（图 12-1（a、 b））如解除简支梁的右端铰支座，或解除悬臂梁固端对转动约束，使之成为铰支座，则此时 的梁变成了图 12.1（c）的可动机构，是几何可变系不能承受横向载荷。在无多余联系的几 何不变的静定系统上增加约束或联系，称为多余约束，并因而产生多余约束反力，则这样的 有多余约束的系统，仅利用静力平衡条件无法求得其反力和内力，称为静不定（或超静定） 系统，如图 12-2。 外静不定：静不定结构的外部支座反力不能全由静力平衡方程求出的情况，常称为外静 不定结构（图 12-2b，d） 内静不定：静不定结构内部约束(或联系)形成的内力不能单由静力平衡方程求出的情况 称为内静不定结构（图 12-2a，c）。 对于内、外静不定兼而有之的结构，有时称为混合静不定结构。 3．静不定次数的确定 1）根据结构约束性质可确定内、外约束力总数，内、外约束力总数与独立静力平衡方 程总数之差即为静不定结构的静不定次数。 2）外静不定的判断：根据结构与受力性质，确定其是空间或是平面承载结构，即可确 定全部约束的个数。根据作用力的类型，可确定独立平衡方程数，二者之差为静不定次数

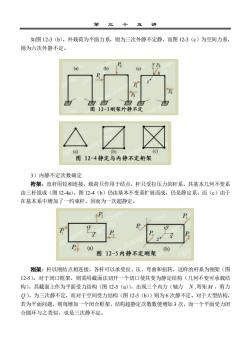
如图12-3（b），外载荷为平面力系，则为三次外静不定静，而图12-3（c）为空间力系则为六次外静不定。P(@)(b)中中中市中中图12-3刚架外静不定A7十图12-4静定与内静不定桁架3）内静不定次数确定桁架：直杆用铰相连接，载荷只作用于结点，杆只受拉压力的杆系，其基本几何不变系由三杆组成（图12-4a)。图12-4（b）仍由基本不变系扩展而成，仍是静定系，而（c）由于在基本系中增加了一约束杆，因而为一次超静定。APP33P(a)(b)图12-5内静不定刚架刚架：杆以刚结点相连接，各杆可以承受拉、压、弯曲和扭转，这样的杆系为刚架（图12-5）。对于闭口框架，则需用截面法切开一个切口使其变为静定结构（几何不变可承载结构），其截面上作为平面受力结构（图12-5（a))，出现三个内力（轴力N，弯矩M，剪力Q），为三次静不定，而对于空间受力结构（图12-5（b））则为6次静不定。对于大型结构，若为平面问题，则每增加一个闭合框架，结构超静定次数数便增加3次，而一个平面受力闭合圆环与之类似，也是三次静不定

第 三 十 五 讲 如图 12-3（b），外载荷为平面力系，则为三次外静不定静，而图 12-3（c）为空间力系， 则为六次外静不定。 3）内静不定次数确定 桁架：直杆用铰相连接，载荷只作用于结点，杆只受拉压力的杆系，其基本几何不变系 由三杆组成（图 12-4a）。图 12-4（b）仍由基本不变系扩展而成，仍是静定系，而（c）由于 在基本系中增加了一约束杆，因而为一次超静定。 刚架：杆以刚结点相连接，各杆可以承受拉、压、弯曲和扭转，这样的杆系为刚架（图 12-5）。对于闭口框架，则需用截面法切开一个切口使其变为静定结构（几何不变可承载结 构），其截面上作为平面受力结构（图 12-5（a）），出现三个内力（轴力 N ,弯矩 M ，剪力 Q ），为三次静不定，而对于空间受力结构（图 12-5（b））则为 6 次静不定。对于大型结构， 若为平面问题，则每增加一个闭合框架，结构超静定次数数便增加 3 次，而一个平面受力闭 合圆环与之类似，也是三次静不定

材料力学教案4）混合静不定次数确定先判断外静不定次数，后判断内静不定次数，二者之和为结构静不定次数。4.基本静定系（静定基），相当系统解除静不定结构的某些约束后得到静定结构，称为原静不定结构的基本静定系（简称静定基）。静定基的选择可根据方便来选取，同一问题可以有不同选择。在静定基上加上外载荷以及多余约束力的系统称为髋不定问题的相当系统。§14-2用力法解静不定结构1.力法与位移法力法：以多余约束力为基本未知量，将变形或位移表示为未知力的函数，通过变形协调条件作为补充方程求来解未知约束力，这种方法称为力法，又叫柔度法。位移法：以结点位移作为基本未知量，将力通过本构关系表示成位移的函数。通过结点平衡条件，解出未知量，这种方法称为位移法，又叫刚度法。本文以力法为主，不涉及位移法。2.力法的基本思路：以一例说明ak例14-1图12-6（a）是车削工件安有尾顶针的简化模型。这是一次静不定，解除B端约束成悬臂梁（静6定基，亦可解除左端转动约束，简化为简支梁），加上BZ多余约束支座反力为X，及外载荷P成相当系统（图P12-6(b))。现求解相当系统中的未知多余约束反力X：在P，X作用下，悬臂梁的B端位移为X@+4A, = Aip + Aixi其中Ar是由于C处作用有外载P引起的B点在X,方向的位移（图(c)，而A1x,是支反力X,引起的图12-6—次静不定梁B点在X,方向的位移（图（d)。因原系统B端是铰支座，在X方向上不应有位移，与原系统比较知相当系统的B点的位移应为零，故(14-1)A, = Aip +Aix = 0这就是协调方程，即得到一个补充方程（补充独立平衡方程不足）在计算Ax,时，可在静定基上沿X,方向作用单位力（图12-6（e）），B点沿X,方向单位力引起的位移为

材 料 力 学 教 案 4）混合静不定次数确定 先判断外静不定次数，后判断内静不定次数，二者之和为结构静不定次数。 4．基本静定系（静定基），相当系统 解除静不定结构的某些约束后得到静定结构，称为原静不定结构的基本静定系（简称静 定基）。静定基的选择可根据方便来选取，同一问题可以有不同选择。 在静定基上加上外载荷以及多余约束力的系统称为静不定问题的相当系统。 §14-2 用力法解静不定结构 1．力法与位移法 力法：以多余约束力为基本未知量，将变形或位移表示为未知力的函数，通过变形协调 条件作为补充方程求来解未知约束力，这种方法称为力法，又叫柔度法。 位移法：以结点位移作为基本未知量，将力通过本构关系表示成位移的函数。通过结点 平衡条件，解出未知量，这种方法称为位移法，又叫刚度法。 本文以力法为主，不涉及位移法。 2．力法的基本思路：以一例说明 例 14-1 图 12-6（a）是车削工件安有尾顶针的简 化模型。这是一次静不定，解除 B 端约束成悬臂梁（静 定基，亦可解除左端转动约束，简化为简支梁），加上 多余约束支座反力为 X1 及外载荷 P 成相当系统（图 12-6（b））。现求解相当系统中的未知多余约束反力 X1： 在 P ， X1 作用下，悬臂梁的 B 端位移为 1 1P 1X1  =  +  其中 1P 是由于 C 处作用有外载 P 引起的 B 点在 X1 方向的位移（图（c）），而 1X1  是支反力 X1 引起的 B 点在 X1 方向的位移（图（d））。因原系统 B 端是铰支 座，在 X1 方向上不应有位移，与原系统比较知相当系统的 B 点的位移应为零，故 0 1 1 1 1  =  P +  X = （14-1） 这就是协调方程，即得到一个补充方程（补充独立平衡方程不足）在计算 1X1  时，可在静 定基上沿 X1 方向作用单位力（图 12-6（e）），B 点沿 X1 方向单位力引起的位移为  11

A对线弹性结构应有：Ax =8X,代入（14-1）有：(14-2)8,X, +Ap=08i与Aip可用莫尔积分或其他方法求得：13-g(l-0) 83ETAIP=由协调方程（14-2）可解得：t=Pa=2%(31-a)求得X,后，则可解出相当系统所有内力、位移，此相当系统的解即原系统的解。3.n次静不定的正则方程可将上述思想推广到n次静不定系统，如解除n个多余约束后的未知多余约束力为X,(=1,2.,n），它们将引起X,作用点的相应的位移为之4，，而原系统由于X（j=1...n)与外载荷共同作用对此位移限制为零（或已知)，故有O,X,+o2X,+..+o.X, +Ap=002X, +022X, ++82,X, +2p=0(14-3)[o.X,+onX,+...+om.X,+Anp=0根据位移互等定理有(14-4)0,=0n8,称为柔度系数，是X，=1引起的X,作用点X,方向上的位移；4,p是外载荷引起的X,处的相应位移。（14-3）称为静不定力法正则方程，它们是对应于n个多余未知力X,的变形协调条件，是求解静不定问题的补充方程

第 三 十 五 讲 对线弹性结构应有： 1X1 =  11X1 代入（14-1）有：  11X1 + 1P = 0 （14-2）  11 与 1P 可用莫尔积分或其他方法求得： EI l 3 3  11 = ， ( l a) EI Pa  P = − 3 − 6 2 1 由协调方程（14-2）可解得： ( l a) l Pa X = 3 − 2 3 2 1 求得 X1 后，则可解出相当系统所有内力、位移，此相当系统的解即原系统的解。 3．n 次静不定的正则方程 可将上述思想推广到 n 次静不定系统，如解除 n 个多余约束后的未知多余约束力为 X ( j n) j = 1,2,., ，它们将引起 Xi 作用点的相应的位移为 = n j ij 1  ，而原系统由于 X ( j , n ) j = 1  与外载荷共同作用对此位移限制为零（或已知），故有          + +  + +  =   + +  + +  = + +  + +  = 0 0 0 1 1 2 2 21 1 22 2 2 2 11 1 12 2 1 1 n n nn n nP n n P n n P X X X X X X X X X          (14-3) 根据位移互等定理有  ij =  ji （14-4）  ij 称为柔度系数，是 X j = 1 引起的 Xi 作用点 Xi 方向上的位移；  iP 是外载荷引起 的 Xi 处的相应位移。（14-3）称为静不定力法正则方程，它们是对应于 n 个多余未知力 Xi 的 变形协调条件，是求解静不定问题的补充方程

材料力学教案例14-2图12-7（a）所示为一静不定刚架，设两杆EI相同。解：为三次静不定结构，解除B端约束，代之以多余约束反力X，X,，X，图（b）为相当系统，按式（12-3），8g、A,均可用莫尔定理计算，即有：qaI adx,=-Ap=EIJO6EI9qat1ragx2A2p =Ed8EIgq3F[1d=Asp=-E26EI(@)(f图12-7静不定刚架的求解-**+[--m3EIo2=d=号3EI-++F6:-60-- -=2EI-+++2EI-0-*--2EI将以上值代入（14-3)，整理后得8aX, +3aX2 +9X, = qa212aX +8aX, +12X, = 3qa2

材 料 力 学 教 案 例 14-2 图 12-7（a）所示为一静不定刚架，设两杆 EI 相同。 解：为三次静不定结构，解除 B 端约束，代之以多余约束反力 X1，X2 ，X 3 ，图（b） 为相当系统，按式（12-3），  ij 、iP 均可用莫尔定理计算，即有： EI qa adx qx EI a P 2 6 1 4 0 2 2 2 1 = −  = − EI qa x dx qx EI a P 2 8 1 4 0 2 2 2 2 2 = − = −  EI qa dx qx EI a P 6 1 2 1 3 0 2 2 2 3 = −  = −   EI a dx EI x x dx EI a a 3 4 1 1 1 1 3 0 0 11 = 1  1 1 +   =    EI a x x dx EI a 3 1 3 0 22 = 2  2 2 =   EI a dx EI dx EI a a 2 1 1 1 1 1 1 0 0 33 =   1 +   =    EI a x adx EI a 2 1 3 0 12 = 21 = 2  2 =    EI a a dx EI x dx EI a l 2 3 1 1 1 1 2 0 2 0 13 = 31 = 1   1 +   =     EI a x xdx EI a 2 1 2 0 23 = 32 = 2  2 =    将以上值代入（14-3），整理后得 2 8aX1 + 3aX2 + 9X3 = qa 2 12aX1 + 8aX2 +12X3 = 3qa

讲五9aX +3aX, +12X, = qa解此联立方程，求出X=-%X- X-%161648式中负号表示X与所设方向相反，应向下。求出多余约束力，即求出了支座B的支反力，进一步即可作出内力图

第 三 十 五 讲 2 9aX1 + 3aX2 +12X3 = qa 解此联立方程，求出 16 1 qa X = − ， 16 7 2 qa X = ， 48 2 3 qa X = 式中负号表示 X1 与所设方向相反，应向下。求出多余约束力，即求出了支座 B 的支反力， 进一步即可作出内力图