内蒙古科技大学：《材料力学》课程授课教案（讲义）第33讲 能量法（Ⅱ）

材料力学教案第33讲教学方案能量法（I）基本1. 功的互等定理与位移互等定理。内2.卡氏定理。容教掌握功的互等定理的推导方法及其应用。学目2掌握位移互等定理的推导方法及其应用。的3掌握卡氏第一定理的推导方法及其应用。4.掌握卡氏第二定理的推导方法及其应用。5：了解虚功原理其应用。1.重点掌握功的互等定理的推导方法及其应用点2重点掌握位移互等定理的推导方法及其应用。难3.要求掌握卡氏第二定理的推导方法及其应用。点4.难点之一是如何正确应用卡氏第二定理5，难点之二是在应用卡氏第二定理时，虚载荷法的应用。本次教学计划学时：2学时。教学课堂讨论：安1.功的互等定理与位移互等定理之间的关系。排2．卡氏第一定理与卡氏第二定理有什么关系，在应用上有什么不同？3.虚功原理有什么用途？

材 料 力 学 教 案 第 33 讲 教学方案 —— 能量法（Ⅱ） 基 本 内 容 1. 功的互等定理与位移互等定理。 2. 卡氏定理。 教 学 目 的 1. 掌握功的互等定理的推导方法及其应用。 2. 掌握位移互等定理的推导方法及其应用 。 3. 掌握卡氏第一定理的推导方法及其应用。 4. 掌握卡氏第二定理的推导方法及其应用。 5． 了解虚功原理其应用。 重 点 、 难 点 1. 重点掌握功的互等定理的推导方法及其应用 。 2. 重点掌握位移互等定理的推导方法及其应用 。 3. 要求掌握卡氏第二定理的推导方法及其应用 。 4. 难点之一是如何正确应用卡氏第二定理 。 5． 难点之二是在应用卡氏第二定理时，虚载荷法的应用。 教 学 安 排 本次教学计划学时：2 学时。 课堂讨论： 1. 功的互等定理与位移互等定理之间的关系。 2. 卡氏第一定理与卡氏第二定理有什么关系，在应用上有什 么不同？ 3. 虚功原理有什么用途？

第三十三讲卡氏定理与莫尔积分有什么关系？在应用时各有什么限4.制?

第 三 十 三 讲 4． 卡氏定理与莫尔积分有什么关系？在应用时各有什么限 制？

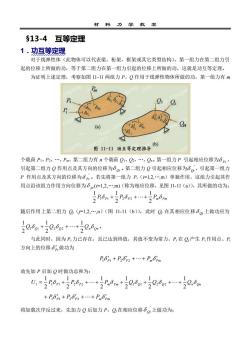
学教室513-4互等定理1.功互等定理对于线弹性体（此物体可以代表梁，桁架，框架或其它类型结构），第一组力在第二组力引起的位移上所做的功，等于第二组力在第一组力引起的位移上所做的功，这就是功互等定理。为证明上述定理，考察如图11-11两组力P，Q作用于线弹性物体所做的功，第一组力有mPm86BarQ0.a图 11-11 功互等定理推导 (6)个载荷Pi，P2，…，Pm，第二组力有n个载荷Oi，Q2，，Qn。第一组力P引起相应位移为pr引起第二组力Q作用点及其方向的位移为80。第二组力Q引起相应位移为，引起第一组力P作用点及其方向的位移为8p。若先将第一组力P;（i=1,2,,m）单独作用，这组力引起其作用点沿该组力作用方向位移为8(i=1,2,,m）（称为相应位移，见图11-11（a))，其所做的功为：1POp+POp2+..+P.opm随后作用上第二组力（=1,2,,n）（图11-11（b)，此时Q在其相应位移8上做功应为10,0+0,00 -O,oon与此同时，因为P,力已存在，且已达到终值，其值不变为常力，P在9,产生P:作用点、P方向上的位移8,做功为Popr+P,op2 +...+Pmopm故先加P后加Q时做功总和为：Upoppoom00o+.0o2++ooo+Popr +P,op2 +..+P.opm将加载次序反过来，先加力Q后加力P，在相应位移上做功为：

材 料 力 学 教 案 §13-4 互等定理 1．功互等定理 对于线弹性体（此物体可以代表梁，桁架，框架或其它类型结构），第一组力在第二组力引 起的位移上所做的功，等于第二组力在第一组力引起的位移上所做的功，这就是功互等定理。 为证明上述定理，考察如图 11-11 两组力 P，Q 作用于线弹性物体所做的功，第一组力有 m 个载荷 P1，P2，.，Pm，第二组力有 n 个载荷 Q1，Q2，.，Qn。第一组力 P 引起相应位移为  Pi ， 引起第二组力 Q 作用点及其方向的位移为  Qi 。第二组力 Q 引起相应位移为 '  Qi ，引起第一组力 P 作用点及其方向的位移为 '  Pi 。若先将第一组力 Pi（i=1,2,.,m）单独作用，这组力引起其作 用点沿该组力作用方向位移为  pi (i=1,2,.,m)（称为相应位移，见图 11-11（a）），其所做的功为： P P P  P Pm Pm 2 1 2 1 2 1 1 1 + 2 2 ++ 随后作用上第二组力 Qj（j=1,2,.,n）（图 11-11（b）），此时 Qj 在其相应位移  Qj 上做功应为 Q  Q Q  Q Qn Qn 2 1 2 1 2 1 1 1 + 2 2 ++ 。 与此同时，因为 Pi 力已存在，且已达到终值，其值不变为常力，Pi 在 Qj 产生 Pi 作用点、Pi 方向上的位移  Pi  做功为 P P P  P Pm Pm  +  ++  1 1 2 2 故先加 P 后加 Q 时做功总和为： U P P P  P Pm P m Q  Q Q  Q Qn Qn 2 1 2 1 2 1 2 1 2 1 2 1 1 = 1 1 + 2 2 ++ + 1 1 + 2 2 ++ P P P  P Pm Pm +  +  ++  1 1 2 2 将加载次序反过来，先加力 Q 后加力 P，Qj 在相应位移 '  Qi 上做功为：

第1000+0.00+++0.8om再加P(i=1,2"m)力，P,在其相应位移8，做功为：pom+Pop+P.om同时物体上已作用有の且其值不变，Q,在由于P引起的Q,作用点及方向的位移80,上做功为：Q001 +Q,002 +...+Q,0om对此加载顺序，两组力所做的总功为：Upompom.om0oo.+=0,+Q01+Q2002+...+Q.0由于变形能只决定于力与位移的最终值，与加力次序无关，故必有U=U2，从而得功互等定理的表达式为：(13-18)Pop +P,Sp2+...+P.Sm=Q801 +O,0o2 +...+O0on2.位移豆等定理利用（11-18），并设两组力各只有一个力P、,作用于同一物体，则有：P,8"=0,80若P,=Q,，则有0p=00l若将Q引起P，相应位移写成8，将P引起的相应于Q，的位移写成8，则上式又可写成常用的公式0F8.(13-19)此式即为位移互等定理：Pi作用点沿Pi方向由于Q，而引起Rs的位移8，等于，作用点沿，方向由于Pi引起的位移O i.上述互等定理中的力与位移都应理解为广义的，如果力换成力偶，则相应的位移应是转角位移，其推导不变。X=l例题13-4装有尾顶针的车削工件可简化成超静定梁图11-12静不定采如图11-12，试用互等定理求解

第 三 十 三 讲 ' n Qn ' Q ' Q  Q Q  Q  2 1 2 1 2 1 1 1+ 2 2++ 再加 Pi (i=1,2,.,m)力，Pi 在其相应位移  Pi 做功为： P P P  P Pm Pm 2 1 2 1 2 1 1 1 + 2 2 ++ 同时物体上已作用有 Qj 且其值不变，Qj 在由于 Pi 引起的 Qj 作用点及方向的位移  Qj 上做功为： Q1 Q1 + Q2 Q2 ++ Qn Qn 对此加载顺序，两组力所做的总功为： U P P P  P Pm Pm 2 1 2 1 2 1 2 = 1 1 + 2 2 ++ Q  Q Q  Q Qn Qn +  +  + +  2 1 2 1 2 1 1 1 2 2  由于变形能只决定于力与位移的最终值，与加力次序无关，故必有 U1=U2，从而得功互等定理的 表达式为： P P P  P Pm Pm  +  ++  1 1 2 2 =Q1 Q1 + Q2 Q2 ++ Qn Qn （13-18） 2．位移互等定理 利用（11-18），并设两组力各只有一个力 Pi、Qj 作用于同一物体，则有： Pi Pi = Qj Qj  若 Pi = Qj ，则有  P1 =  Q1  若将 Q j 引起 Pi 相应位移写成  ij ，将 Pi 引起的相应于 Q j 的位移写成  ji ， 则上式又可写成常 用的公式  ij = ji （13-19） 此式即为位移互等定理：Pi 作用点沿 Pi 方向由于 Q j 而引起 的位移  ij ，等于 Q j 作用点沿 Q j 方向由于 Pi 引起的位移  ji。 上述互等定理中的力与位移都应理解为广义的，如果力 换成力偶，则相应的位移应是转角位移，其推导不变。 例题 13-4 装有尾顶针的车削工件可简化成超静定梁 如图 11-12，试用互等定理求解。 + Q1 Q1 + Q2 Q2 ++ Qn Qn

材料力学教察解：解除支座B，把工件看成悬臂梁，将切削力P及顶针反力RB作为第一组力，设想在同一悬臂梁右端作用单位力X=1，作为第二组力。在X-1作用下悬臂梁上的P及RB作用点的相应位移分别为（图11-12(b)13sd =(31 -a),8, =6EI3EI第一组力在第二组力引起的位移上所做的功为：Pea (1 -a)-Re13P81 -R82 :3EI6EI第一组力作用下，其右端B实际位移为零，所以第二组力在第一组力引起的位移上所做的功等于零。由功互等定理有：Re13ga-=03EIPa?由此解得：R(31 -a)21$13-5卡氏定理1.卡氏第一定理弹性杆件的应变能U(8)对于杆件上与某一载荷相应的位移8（i=1,2,n）的变化率等于该载荷的值，即：oU=P.(13-20)08,以图11-13简支梁为例，其上作用有载荷P1，P2，，P。（广义力），其相应位移为81，82，…，8n（广义位移）。假定载荷P（i-1,2,,n）同时作用，且由同一比例从零加载到终值Pi（i=1,2,"n)。结构的变形能P,ds,等于载荷作用期间所做的功，通过材料的载荷一位移关系每个力P,可表成为其相应位移8,的函数，通过积分求得的变形能是位移8的函数，即U(8.)如果此时某一位移8,有一增量d,，其余位移保持不变，则此时变形能的增量dU为：au -%u do.BP.BPasA1000图11-13简支梁上的广义与广义位移

材 料 力 学 教 案 解：解除支座 B，把工件看成悬臂梁，将切削力 P 及顶针反力 RB 作为第一组力，设想在同 一悬臂梁右端作用单位力 X=1，作为第二组力。在 X=1 作用下悬臂梁上的 P 及 RB 作用点的相应 位移分别为（图 11-12（b）） (3 ) 6 2 1 l a EI a  = − , EI l 3 3  2 = 第一组力在第二组力引起的位移上所做的功为： EI R l l a EI Pa P R B B 3 (3 ) 6 2 3  1 −  2 = − − 第一组力作用下，其右端 B 实际位移为零，所以第二组力在第一组力引起的位移上所做的 功等于零。由功互等定理有： 0 3 (3 ) 6 2 3 − − = EI R l l a EI Pa B 由此解得： (3 ) 2 2 2 l a l P a RB = − §13-5 卡氏定理 1．卡氏第一定理 弹性杆件的应变能 U(  i )对于杆件上与某一载荷相应的位移  i （i=1,2,.,n）的变化率等于 该载荷的值，即： i i P U =    （13-20） 以图 11-13 简支梁为例，其上作用有载荷 P1，P2，.，Pn（广义力），其相应位移为δ1，δ 2，.，δn（广义位移）。假定载荷 Pi（i=1,2,.,n）同时作用，且由同一比例从零加载到终值 Pi（i=1,2,.,n）。结构的变形能 Pid i 等于载荷作用期间所做的功，通过材料的载荷—位移关系， 每个力 Pi 可表成为其相应位移  i 的函数，通过积分求得的变形能是位移δ的函数，即 ( ) U  i 如果此时某—位移  i 有一增量 i d ，其余位移保持不变，则此时变形能的增量 dU 为: i i d U dU    =

第I当位移s,增大ds,时，相应力P:将做功Pd8,，而其它任何力都不做功，因为其它的位移没有改变，：.dW=Pds，根据（13-1）dU=dW故有：P=OU08.卡氏第一定理还可通过鹰位移愿导出，不受线弹性材料的限制，可用于非线性弹性材料杆件或结构。2.卡氏第二定理线弹性杆件或杆系的应变能U（P）对于作用在该杆件或杆系上的某一载荷的变化率等于该载荷相应的位移，即：oU=8.(13-21)ap,弹性结构，在外力P.P...P.…作用下，其相应的位移为..82，…，8.….结构的应变能是Pi，P2，…，Pi，…的函数，即U(P)设诸力中只有P有一个增量P，其余不变，则相应产生位移增量，8,，…，,，…，此时功的增量，亦即应变能增量为（略去高阶小量三AP,A5,）。AU -PA, + P,A, +..+ PAO, +..将原作用力Pi，P2，…，P，…作为第一组力，把△P,看作第二组力，则由劲互等定理，得：PAo, + P,AS, +...+ PAS, +..=P,o.所以有：AU = AP,8,岁-0或若△P趋近于零，则：4U-OU=8limP,"aP这就是卡氏第二定理表达式

第 三 十 三 讲 当位移  i 增大 i d 时，相应力 Pi 将做功 Pid i ，而其它任何力都不做功，因为其它的位移 没有改变，∴ dW = Pid i ，根据（13-1） dU = dW 故有： i i U P   = 卡氏第一定理还可通过虚位移原理导出，不受线弹性材料的限制，可用于非线性弹性材料杆 件或结构。 2．卡氏第二定理 线弹性杆件或杆系的应变能 U（ Pi ）对于作用在该杆件或杆系上的某一载荷的变化率等于 该载荷相应的位移，即： i Pi U =    （13-21） 弹性结构，在外力 P1，P2，.，Pi，.作用下，其相应的位移为δ1，δ2，.，δi，.， 结构的应变能是 P1，P2，.，Pi，.的函数，即 ( ) U Pi 设诸力中只有 Pi 有一个增量 Pi ，其余不变，则相应产生位移增量  1， 2 ，.，  i ，.， 此时功的增量，亦即应变能增量为（略去高阶小量 Pi i 2 1 ）。 U = P1 1 + P2 2 ++ Pi i + 将原作用力 P1，P2，.，Pi，.作为第一组力，把 Pi 看作第二组力，则由功互等定理，得： P1 1 + P2 2 ++ Pi i += Pi i 所以有： U = Pi i 或 i Pi U =    若 Pi 趋近于零，则： i P i Pi U P U i     =   = → lim 0 这就是卡氏第二定理表达式

材料力学教察对于横力弯曲，应变能用（13-12），用卡氏定理，有： -%-(rM)-[M M d(13-21a)apapJi2EI=JEIap,对于桁架、拉、压杆，应用（13-6)8, -%-()NION(13-21b)PaP台2EA）台EA，P例题13-5图11-14外伸梁抗弯刚度为EI，试求外伸端C的挠度fec和左端截面的转角 0 A。解：外伸端C作用有集中力P，截面4作用有集中力偶矩m，根据卡氏第二定理有：.-0U- M) oMadP= JEInap. -u - Ma aM(n dOmJEIomX弯矩应分段表达：AB段图11-14求外伸梁加力点位移m_PaM,(x)=R,x, -m:aM(x)=-XpOM(x)_ -1OmTaM,(x2) =0aM,(x2)BC段： M,(xz)=-Px2,X2apomf.=%-[(m-Pg)x-m(-9x )db则:5=JEi(1apPa'l+mal+Pa"-Px+J(-x )d, 2FI236r[(m_ Pa)au-m[-1]dOA:Rom-JoEi(7

材 料 力 学 教 案 对于横力弯曲，应变能用（13-12），用卡氏定理，有：     =          =   = l i l i i i dx P M x EI M x EI M x dx P P U ( ) ( ) 2 ( ) 2  （13-21a） 对于桁架、拉、压杆，应用（13-6）   = =   =           =   = n j j j j j j n j j j j i i i P N EA N l EA N l P P U 1 1 2 2  （13-21b） 例题 13-5 图 11-14 外伸梁抗弯刚度为 EI，试求外伸端 C 的挠度 fC和左端截面的转角θA。 解：外伸端 C 作用有集中力 P，截面 A 作用有集中力偶矩 m，根据卡氏第二定理有： dx P M x EI M x P U f l c   =   =  ( ) ( ) dx m M x EI M x m U l A   =   =  ( ) ( )  弯矩应分段表达： AB 段： x m l P a l m M x R x m c A  −      1 1 = 1 − = − 1 ( ) 1 1 1 ( ) x l a P M x = −   1 ( ) 1 1 1 = −   l x m M x BC 段： 2 2 2 M (x ) = −Px ， 2 2 2 ( ) x P M x = −   ， 0 ( ) 2 2 =   m M x 则：         −        −      = −   = l c c x dx l a x m l P a l m P EI U f 0 1 1 1 1 2 2 0 2 ( x )dx EI a Px − − +          = + + 3 6 3 1 2 2 Pa l mal Pa EI 1 1 1 0 1 1 dx l x x m l P a l m m EI U c l A       −        −      = −   =  

第I1(ml,Pal)+(-Px) (0)dx =-E(36)这里fc与0A皆为正号，表示它们的方向分别与P和m作用方向相同，而如果是负号，则表示与之方向相反。用卡氏定理求结构某处的位移时，该处需要有与所求位移相应的载荷，如果计算某处位移而该处没有与此位移相应的载荷，则可采用附加力法（见例11-6)。例题13-6线弹性材料悬臂梁，自由端A作用有集中力（图11-15)，若P、1、EI已知试求：1）加力点A的位移8A：2）非加力点B的位移8B。解：（1）求加力点A的位移，用卡氏第二定理：ABEIGaPPTJoELaPapamBECM=-Px,A-Ox代入上式得：图11-15求位移的附加力法1()-%3EIau(2)求非加力点B的位移时，可在B点附加力P,仍用fs=，有附加力P'后弯矩为：-apr%=0 BC段： M, --Px-P(x--)AB段：M=-Px，ap'[Px-P(x-1/2) (-(x-1/2)x.. fe=EIPlx-)Palx-4)5PI3PP2)dx=2)dx·+48EI*24EIEIEI因为实际上B处并无力作用，故应令上式中的P'=0才是实际情况下B处位移，故-由以上计算可见，在加附加力计算非加力点位移时，只要在计算%鼻%时考虑附加力，而在M(x)中，可令P'=0，则积分计算可以简化

第 三 十 三 讲  + −  a Px dx EI 0 1 ( ) (0) 1       = + 3 6 1 ml Pal EI 这里 fC与θA 皆为正号，表示它们的方向分别与 P 和 m 作用方向相同，而如果是负号，则表 示与之方向相反。 用卡氏定理求结构某处的位移时，该处需要有与所求位移相应的载荷，如果计算某处位移， 而该处没有与此位移相应的载荷，则可采用附加力法（见例 11-6）。 例题 13-6 线弹性材料悬臂梁，自由端 A 作用有集中力（图 11-15），若 P、l、EI 已知， 试求：1）加力点 A 的位移δA；2）非加力点 B 的位移δB。 解：（1）求加力点 A 的位移，用卡氏第二定理：    =    = l A dx P M EI M P U f 0 M = −Px， x x M = −   代入上式得： EI Pl x dx EI Px f l A 3 ( ) 3 0 − = − =  （2）求非加力点 B 的位移时，可在 B 点附加力 P ,仍用 P U f B    = ，有附加力 P 后弯矩为： AB 段： M = −Px 1 ， 0 1 =    P M BC 段：       = − −  − 2 2 l M Px P x ， ) 2 ( 1 l x P M = − −    ∴  ( )  (x l )dx EI Px P x l f l l B 2 2 2  − − − −  − =           −  +       − = l l l l dx EI l P x dx EI l Px x 2 2 2 2 2 EI P l EI Pl 48 24 5 3 3  = + 因为实际上 B 处并无力作用，故应令上式中的 P = 0 才是实际情况下 B 处位移，故 EI Pl f B 48 5 3 = 由以上计算可见，在加附加力计算非加力点位移时，只要在计算 P U    时考虑附加力，而在 M(x)中，可令 P = 0 ，则积分计算可以简化

料力学教案$13-6虚功原理囊位稳指的是弹性体（或结构系）的附加的满足约束条件及连续条件的无限小可能位移。所谓虚位移的“虚”字表示它可以与真实的受力结构的变形而产生的真实位移无关，而可能由于其它原因（如温度变化，或其它外力系，或是其它干扰）造成的满足位移约束、连续条件的几何可能位移。对于虚位移要求是微小位移，即要求在产生虚位移过程中不改变原受力平衡体的力的作用方向与大小，亦即受力平衡体平衡状态不因产生虚位移而改变。真实力在虚位移上做的功称为虚功襄功愿理又称虚位移原理：如果给在载荷系作用下处于平衡的可变形结构以微小虚位移，则外力系在虚位移上所做的虚功等于内力在相应虚变形上所做的虚功，即：(13-22a)W.=W,虚功原理可以用梁的例子给出其表达式和原理的证Pin明：图11-16，11-17（a）梁受外力 P1，P2，…，P及分A布载荷g()作用而处于平衡。在给此梁任一虚位移时，所x有载荷作用点均有沿其作用方向的虚位移，，…，，图11-16受力染及虚位移原理v（x)，于是外力在相应虚位移上的总虚功为：W = Pyi + Pv, +.-+ P,v, + q(x)v(x)dx另一方面，梁内力对于虚位移所做的虚功，可PiPPPPn从梁中取出任一微段d（图11-17（b））来大研究，微段左、右截面上内力有：剪力Q.Q+dQ,Hdo弯矩M、M+dM，轴力N、N+dN，扭矩T、T+dT,MO对微段，这些力可看作是外力。微段的虚位移TdrM可分为刚体虚位移和变形虚位移，在载荷作用Odo下梁所有微段都会发生变形，所研究微段因其arFa余各微段变形而发生虚位移，就是此微段的刚do体虚位移，而由于该微段本身变形所引起的虚T婆d位移称为变形虚位移。由于微段处于平衡状态，由质点系虚位移原理知，所有外力对于该微段d2:a的刚体虚位移所做的总虚功必等于零。而该微ardxd段的变形虚位移为图 11-17(c)、(d)、(e)、()图11-17受力悬臂染与虚位移原理的推导所示，此时轴力、弯矩、剪力、扭矩在变形虚位移上所做的虚功为（略去高阶小量）

材 料 力 学 教 案 §13-6 虚功原理 虚位移指的是弹性体（或结构系）的附加的满足约束条件及连续条件的无限小可能位移。所 谓虚位移的“虚”字表示它可以与真实的受力结构的变形而产生的真实位移无关，而可能由于其 它原因（如温度变化，或其它外力系，或是其它干扰）造成的满足位移约束、连续条件的几何可 能位移。对于虚位移要求是微小位移，即要求在产生虚位移过程中不改变原受力平衡体的力的作 用方向与大小，亦即受力平衡体平衡状态不因产生虚位移而改变。真实力在虚位移上做的功称为 虚功。 虚功原理又称虚位移原理：如果给在载荷系作用下处于平衡的可变形结构以微小虚位移，则 外力系在虚位移上所做的虚功等于内力在相应虚变形上所做的虚功，即： We = Wi （13-22a） 虚功原理可以用梁的例子给出其表达式和原理的证 明：图 11-16，11-17（a）梁受外力 P1，P2，.，Pn 及分 布载荷 q(x)作用而处于平衡。在给此梁任一虚位移时，所 有载荷作用点均有沿其作用方向的虚位移 * 1 v ， * 2 v ，.， * n v ， ( ) * v x ，于是外力在相应虚位移上的总虚功为：  = + + + + l We Pv P v Pn vn q(x)v (x)dx * * * 2 2 * 1 1  另一方面，梁内力对于虚位移所做的虚功，可 从梁中取出任一微段 dx（图 11-17（b））来 研究，微段左、右截面上内力有：剪力 Q、Q+dQ， 弯矩 M、M+dM，轴力 N、N+dN，扭矩 T、T+dT， 对微段，这些力可看作是外力。微段的虚位移 可分为刚体虚位移和变形虚位移，在载荷作用 下梁所有微段都会发生变形，所研究微段因其 余各微段变形而发生虚位移，就是此微段的刚 体虚位移，而由于该微段本身变形所引起的虚 位移称为变形虚位移。由于微段处于平衡状态， 由质点系虚位移原理知，所有外力对于该微段 的刚体虚位移所做的总虚功必等于零。而该微 段的变形虚位移为图 11-17（c）、（d）、（e）、（f） 所示，此时轴力、弯矩、剪力、扭矩在变形虚 位移上所做的虚功为（略去高阶小量）：

第==讲W, = J,(mdo+Qda+ Nds + Tdg)根据能量守恒，这两个总虚功相等，故有：Py +Py2 ++ P,v, +Jg(x)(a)dx=[Nd()" +[Mde'+[odt' +[Tdo(13-22b)在导出虚功原理时，并没有涉及应力一应变关系，因此与材料性质无关，故这一原理可用于线性弹性材料，也可用于非线性应力一应变关系的材料

第 三 十 三 讲 W (md Qd Nd Td) l i = + + +  根据能量守恒，这两个总虚功相等，故有：  + + + + l Pv P v Pn vn q(x)v (x)dx * * * 2 2 * 1 1      =  + + + * * * * Nd( l) Md Qd Td （13-22b） 在导出虚功原理时，并没有涉及应力—应变关系，因此与材料性质无关，故这一原理可用于 线性弹性材料，也可用于非线性应力—应变关系的材料