内蒙古科技大学：《材料力学》课程教学资源（习题解答）拉伸、压缩与剪切

2.1．试求图示各杆1-1、2-2、3-3截面的轴力，并作轴力图。-.-.解: (a)(1)求约束反力OKNKNIZX=0-R+40+3020=0R=50kN(2)求截面 1-1 的轴力ZX=0 -R+N,=0N,=50kN(3)求截面2-2的轴力OkNZX=0-R+40+N,=0N, =10kN(4)求截面 3-3的轴力Zx=0N,=-20KN(5)画轴力图N(KN)50

2.1. 试求图示各杆 1-1、2-2、3-3 截面的轴力， 并作轴力图。 3 1 1 3 2 40kN 2 20kN 30kN (a) 1 1 2 2 3 3 4P P (b) 解: (a) (1)求约束反力 3 1 1 3 2 40kN 2 20kN 30kN R R kN RX 50 0203040 0 = ∑ = − + + − = (2)求截面 1-1 的轴力 N1 1 1 R kNN NRX 50 0 0 1 1 = ∑ = − + = (3)求截面 2-2 的轴力 40kN 2 2 R N2 kNN NRX 10 040 0 2 2 = ∑ = − + + = (4)求截面 3-3 的轴力 3 3 20kN N3 3 3 0 20 0 20 X N N kN = −− = = − ∑ (5)画轴力图 x －20 10 50 N ( KN ) (+) (-)

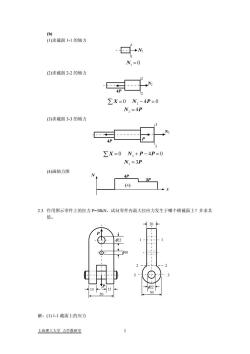
(b) (1)求截面 1-1 的轴力V(2)求截面 2-2 的轴力ZX=0 N,-4P=0N, =4P(3)求截面 3-3 的轴力ZX=0 N,+P-4P=0N, =3P(4)画轴力图(+)2.3.作用图示零件上的拉力P=38kN，试问零件内最大拉应力发生于哪个横截面上？并求其值。解：(1)1-1截面上的应力上海理工大学力学教研室

(b) (1)求截面 1-1 的轴力 1 1 N1 0 N1 = (2)求截面 2-2 的轴力 2 2 N2 4P PN PNX 4 04 0 2 2 = ∑ = − = (3)求截面 3-3 的轴力 N3 3 3 P 4P PN PPNX 3 0 04 3 3 = ∑ = + − = (4)画轴力图 x N (+) 4P 3P 2.3. 作用图示零件上的拉力 P=38kN，试问零件内最大拉应力发生于哪个横截面上？并求其 值。 P P 50 15 15 φ22 φ10 50 φ22 20 2 2 3 3 1 1 解：(1) 1-1 截面上的应力 上海理工大学 力学教研室 1

38×10367.86MPaA(50-22)×20×10-(2)2-2截面上的应力38x103=63.33MPa42×15×20×10-6(3)3-3截面上的应力P38×103=45.24MPa.A(50-22)×15×2×10-(4）最大拉应力在1-1截面上0 mx =0,=67.86MPa2.4.设图示结构的1和2两部分皆为刚体，钢拉杆BC的横截面直径为10mm，试求拉杆内的应力。解：（1）以刚体CAEZm =0 N, ×4.5+N.×1.5-P×3=0(2）以刚体 BDE为研究对象Zm,=0N,x1.5-N,×0.75=0上海理工大学力学教研室

1 6 1 3 38 10 67.86 (50 22) 20 10 P MPa A σ − × = = = − ×× (2) 2-2 截面上的应力 3 2 6 2 38 10 63.33 2 15 20 10 P MPa A σ − × = = = ×× × (3) 3-3 截面上的应力 3 3 6 3 38 10 45.24 (50 22) 15 2 10 P MPa A σ − × = = = − × ×× (4) 最大拉应力在 1-1 截面上 86.67 MPa max =σσ 1 = 2.4. 设图示结构的 1 和 2 两部分皆为刚体，钢拉杆 BC 的横截面直径为 10mm，试求拉杆内 的应力。 D C B A P=7.5kN G E 3m 0.75m 1.5m 1.5m 1.5m 1 2 解：(1) 以刚体 CAE 为研究对象 NC NE’ G E C A 3m 1.5m P=7.5kN 1.5m ∑ = × + × − × = 035.15.4 0 ' A Nm E C PN (2) 以刚体 BDE 为研究对象 ∑ = × − × = 075.05.1 0 D E NNm B NE D B E 0.75m NB 1.5m 上海理工大学 力学教研室 2

(3）联立求解N.=N. N,=Ne.N=6kN(4）拉杆内的应力6×103NR76.4MPa元×0.01/4A2.5.图示结构中，杆1、2的横截面直径分别为10mm和20mm，试求两杆内的应力。解：(1）以整体为研究对象，易见A处的水平约束反力为零；(2）以AB为研究对象(B处不带销钉)专IYe由平衡方程知X,=Y,=R, =0(3)以杆 BD 为研究对象OkM由平衡方程求得Zmc=0N,×1-10×1=0N, =10KNZY=0 N,-N,-10-0N, =20KN(4)杆内的应力为上海理工大学力学教研室

(3) 联立求解 kNN NNNN C B C E E 6 ' =∴ = = (4) 拉杆内的应力 3 2 6 10 76.4 0.01 / 4 NB MPa A σ π × == = × 2.5.图示结构中，杆 1、2 的横截面直径分别为 10mm 和 20mm，试求两杆内的应力。 解：(1) 以整体为研究对象，易见 A 处的水平约束反力为零； (2) 以 AB 为研究对象(B 处不带销钉) 由平衡方程知 = = = 0 RYX ABB (3) 以杆 BD 为研究对象 由平衡方程求得 KNN NNY KNN C Nm 20 0 010 10 01101 0 2 12 1 1 = =−−= = = × − × = ∑ ∑ (4) 杆内的应力为 B N2 N1 1m 1m D C 10kN XBB B A YBB RA 2 1 B A 1m 1m D C 10kN 1.5m 1.5m 1.5m 上海理工大学 力学教研室 3

10×10127MPa元×0.01/4A-N_20x10=63.7MPa6元×0.022/42.7.冷镦机的曲柄滑块机构如图所示。镦压工件时连杆接近水平位置，承受的镦压力P=1100kN。连杆的截面为矩形，高与宽之比为h/b=1.4。材料为45钢，许用应力为[o]=58MPa，试确定截面尺寸h和b0解：强度条件为Ss0l又因为A=bh=1.4b，所以b2P1100×103116.4mm1.4[0]1.4×(58×10]h=1.4b≥162.9mm2.8.图示夹紧机构需对工件产生一对20kN的夹紧力，已知水平杆AB及斜杆BC和BD的材料相同，[o]=100MPa，α=30°。试求三杆的横截面直径。解：（1）以杆CO为研究对象S,Zm,(F)=0 N×1-S,×cos30°xl=020×103= 23.1kNS.cOs30°COS300(2)以铰B为研究对象4上海理工大学力学教研室

3 1 1 2 1 3 2 2 2 2 10 10 127 0.01 / 4 20 10 63.7 0.02 / 4 N MPa A N MPa A σ π σ π × == = × × == = × 2.7. 冷镦机的曲柄滑块机构如图所示。镦压工件时连杆接近水平位置，承受的镦压力 P=1100kN 。连杆的截面为矩形，高与宽之比为 h/b=1.4。材料为 45 钢，许用应力为 [σ]=58MPa，试确定截面尺寸 h 和 b。 ：强度条件为 A B b h 解 ≤ σ ][ A P 又因为 A = bh = 1.4b2 , 所以 [ ] ( ) 3 6 1100 10 116.4 1.4 1.4 58 10 1 4 162 9 P b m h . b . mm σ × ≥= = × × = ≥ m 2.8. 图示夹 20kN的夹紧力，已知水平杆AB及斜杆BC和BD的材料 相同，[σ]=100MPa，α=30o 。试求三杆的横截面直径。 ：(1) 以杆 CO 紧机构需对工件产生一对 解 为研究对象 A B P C l l α 工 D 件 α O 0 1 3 1 0 0 ( ) 0 cos30 0 20 10 23.1 cos30 cos30 mF N l S l o N S kN = ×− × ×= × == = ∑ JJG (2) 以铰 B 为研究对象 S1 C N α 上海理工大学 力学教研室 4

=S,=S,=23.1kN（3）由强度条件得三杆的横截面直径4x(23.1×10)4Pdan= d c= dep =17.2mm=元[0]元(100×10)2.10图示简易吊车的杆BC为钢杆，杆AB为木杆，。杆AB的横截面面积4,=100cm2，许用应力[]l=7MPa；杆BC的横截面面积A2=-6cm2，许用应力[ol=160MPa。求许可吊重P。解：（1）以铰B为研究对象，画受力图和封闭的力三角形N, = Pctg30° = V3p=2PN.sin30°(2）由AB杆的强度条件N<[ohEP ≤[0]00)10)-44J3V3(3)由BC杆的强度条件N<[ol2P ≤[0lMA_(6x10-) (160×10)= 48kNPs4x[ol._-22(4)许可吊重[P]= 40.4kN注：BC杆受拉，AB杆受压：BC杆的强度比AB杆的强度高。上海理工大学力学教研室

上海理工大学 力学教研室 5 S1 S2 1 2 P S S kN = = = 23.1 (3) 由强度条件得三杆的横截面直径 ( ) ( ) 3 6 4 4 23.1 10 17.2 [ ] 100 10 AB BC BD P ddd mm π σ π × × === = = × 2.10 图示简易吊车的杆BC为钢杆，杆AB为木杆，。杆AB的横截面面积A1=100cm2 ，许用应力 [σ]1=7MPa；杆BC的横截面面积A2=6cm2 ，许用应力[σ]2=160MPa。求许可吊重P。 解: (1) 以铰 B 为研究对象，画受力图和封闭的力三角形； 1 2 30 3 2 sin 30 o o N Pctg P P N P = = = = (2) 由 AB 杆的强度条件 ( ) ( ) 1 1 1 1 1 3 [ ] [ ] 100 10 3 3 N P A A A P kN σ − × × × ∴≤ = (3) 由 BC 杆的强度条件 1 1 4 6 [ ] 7 10 40.4 ≤ ≤ σ σ × = ( )( ) 2 2 2 2 2 4 6 2 2 2 [ ] [ ] [ ] 6 10 160 10 48 2 2 N P A A A P kN σ σ σ − ≤ ≤ × × ×× ≤ = = (4) 许可吊重 P = 4.40][ kN 注：BC 杆受拉，AB 杆受压；BC 杆的强度比 AB 杆的强度高。 P B S1 S2 P α α C N1 N2 P B 30o 钢 木 B A P P N2 N1 30o

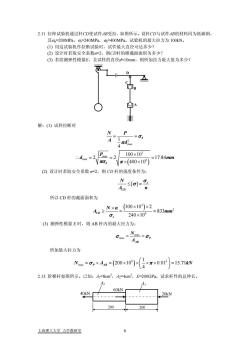
2.11拉伸试验机通过杆CD使试件AB受拉，如图所示。设杆CD与试件AB的材料同为低碳钢，其o=200MPa，a=240MPa，o=400MPa。试验机的最大拉力为100kN。（1）用这试验机作拉断试验时，试件最大直径可达多少？(2）设计时若取安全系数n=2，则CD杆的横截面面积为多少？(3）若欲测弹性模量E，且试样的直径d=10mm，则所加拉力最大值为多少？茶DA解：（1）试样拉断时hA"Trda100×103=17.84mm.d.2元×(400×10%)元0(2）设计时若取安全系数 n=2，则 CD杆的强度条件为：≤[0]=.AcD所以CD杆的截面面积为Ao≥Nxn_ (00x10)x2= 833mm2240×10%a(3）测弹性模量E时，则AB杆内的最大应力为："=o,AAB所加最大拉力为0.012=15.71kNNx =0, ×Ann =(200×10)2.13阶梯杆如图所示。已知：Ai=8cm2，Az=4cm2，E=200GPa。试求杆件的总伸长。A40kN20kN200上海理工大学力学教研室

2.11 件AB受拉，如图所示。设杆CD与试件AB的材料同为低碳钢， 其σp=200MPa，σs=240MPa，σb=400MPa。试验机的最大拉力为 100kN。 (1) 用这试验机作拉断试验时，试件最大直径可达多少？ (2) 设计时若取安全系数n=2，则CD杆的横截面面积为多少？ (3) 若欲测弹性模量E，且试样的直径d=10mm，则所加拉力最大值为多少？ 试样拉断时 拉伸试验机通过杆CD使试 C D B (1) A 解： ( ) 2 max 3 max max 6 1 4 100 10 2 2 17.84 400 10 b b N P A d P d m σ π πσ π = = × ∴= = = × × m (2) 设计时若取安全系数 n=2，则 CD 杆的强度条件为： [ ] s CD N A n σ ≤ = σ 所以 CD 杆的截面面积为 ( ) 3 2 6 100 10 2 833 240 10 CD s N n A mm σ × × × ≥= = × (3) 测弹性模量 E 时，则 AB 杆内的最大应力为： max max P AAB N σ = = σ 所加最大拉力为 ( ) 6 2 max 1 200 10 0.01 15.71 4 N A σ π P AB kN ⎛ ⎞ = × = × × ×× = ⎜ ⎟ ⎝ ⎠ 2.13 阶梯杆如图所示。已知：A1=8cm2 ，A2=4cm2 ，E=200GPa。试求杆件的总伸长。 A A 60kN 40kN 200 200 2 1 20kN 上海理工大学 力学教研室 6

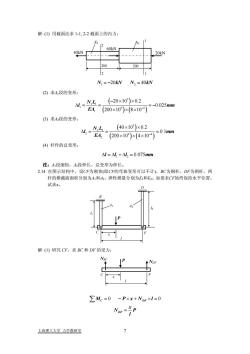
解：(1）用截面法求1-1,2-2截面上的内力：OKN12N,=-20kNN,=40kN(2)求4,段的变形：(-20×10°)×0.2A=N-0.025mmEA(200×10°)×(8×10-)(3）求42段的变形：(40×10)×0.2A=NL-=0.1mmEA(200×10)×(4×10-)(4）杆件的总变形：N= N, +N, =0.075mm注：Ai段缩短，A2段伸长，总变形为伸长。2.14在图示结构中，设CF为刚体(即CF的弯曲变形可以不计)，BC为铜杆，DF为钢杆，两杆的横截面面积分别为A和A2，弹性模量分别为E和E2。如要求CF始终保持水平位置试求x。解：(1）研究CF，求BC和DF的受力ZMc=0-P×x+Npr×l=0Npr==P上海理工大学力学教研室

上海理工大学 力学教研室 7 解: (1) 用截面法求 1-1, 2-2 截面上的内力： A 1 A1 1 2 N kN N kN = − = 20 40 (2) 求A1段的变形： ( ) ( )( ) 3 1 1 1 9 4 1 N L − × 20 10 0.2 0.025 200 10 8 10 l mm EA − × Δ= = = − × ×× (3) 求A2段的变形： ( ) ( )( ) 3 2 2 2 9 4 2 40 10 0.2 0.1 200 10 4 10 N L l m EA − × × Δ= = = × ×× m (4) 杆件的总变形： m 注：A1段缩短，A2段伸长，总变形为伸长。 2.14 在图示结构中，设CF为刚体(即CF的弯曲变形可以不计)，BC为铜杆，DF为钢杆，两 杆的横截面面积分别为A1和A2，弹性模量分别为E1和E2。如要求CF始终保持水平位置， 解: (1 F，求 BC 和 DF 的受力： 1 2 Δ =Δ +Δ = ll l m 0.075 试求x。 ) 研究 C 0 0 DF PxN l x N P l MC D = − × + ×= F = ∑ 60kN 40kN 200 200 2 1 2 2 20kN D P F B l1 l2 A1 A2 C l x P F x C NBC NDF l

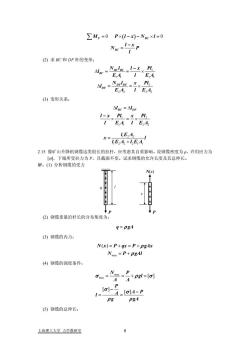
ZM,=0 Px(I-x)-Nece×I=0Nnc=/=p(2)求BC和DF杆的变形；Ne=N=xPFAFAAor=Nerlor=x PE,A."T*E,A(3)变形关系;Al c = NpFxPLPl,1*EATEALE,A*TE.A+,EA'2.15像矿山升降机钢缆这类很长的拉杆，应考虑其自重影响。设钢缆密度为p，许用应力为[o]，下端所受拉力为P，且截面不变。试求钢缆的允许长度及其总伸长。解：(1)分析钢缆的受力TNa)国t0q1目H真VP（2）钢缆重量沿杆长的分布集度为：q=pgA(3）钢缆的内力：N(x) = P+qx= P+ pgAxNmax = P+ pgAl（4）钢缆的强度条件：Nma=+ pgl =[0]gmaxAapgPgA(5）钢缆的总伸长：上海理工大学力学教研室

= 0 ( ) C 0 BC M P xN l l x N P l ×− − = = ∑ (2) 求 BC 和 DF 杆的变形； F B l × − 1 1 1 1 1 2 2 2 2 2 BC BC BC DF DF DF N l l x Pl l E A lE N l x Pl l A E A l EA − Δ= = × Δ = =× (3) 变形关系； 1 2 1 1 2 2 BC DF l l l x Pl x Pl l EA l EA Δ = Δ − × =× 122 1 2 2 2 11 lE A x l lE A lEA = + 2.15 像矿山升降机钢缆这类很长的拉杆，应考虑其自重影响。设钢缆密度为 ρ，许用应力为 [σ]，下端所受拉力为 P，且截面不变。试求钢缆的允许长度及其总伸长。 解：(1) 分析钢缆的受力 (2) 钢缆重量沿杆长的分布集度为： q gA = ρ (3) 钢缆的内力： max N x P qx P ( ) gAx N P gAl ρ ρ = + =+ = + (4) 钢缆的强度条件： max max [ ] [ ] [ ] N P gl A A P A A P l g gA σ ρ σ σ σ ρ ρ = =+ = − − = = (5) 钢缆的总伸长： P l P N(x) q x 上海理工大学 力学教研室 8

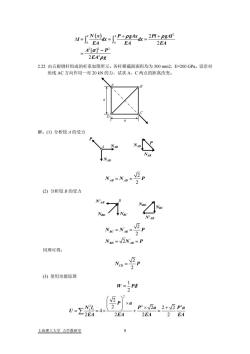
-ra- EA2EA= A[o} - p?2EApg2.22由五根钢杆组成的杆系如图所示。各杆横截面面积均为500mm2，E=200GPa。设沿对角线AC方向作用一对20kN的力，试求A、C两点的距离改变。解：（1）分析铰A的受力DNaNNARNABINADS.Nn=NAD=Y(2）分析铰B的受力V'AENep/NVepNBCN'ABNc=Na-pNeD = V2NAs = P同理可得：Nop(3）使用功能原理W-↓p8++ P×2a_ 2+ 2 pa-2岁-42EA2EA2EA上海理工大学力学教研室9

( ) 2 0 0 22 2 2 2 2 [ ] 2 l l N x P gAx Pl gAl l dx dx EA EA EA A P EA g ρ ρ σ ρ + + Δ= = = − = ∫ ∫ 2.22 由五根钢杆组成的杆系如图所示。各杆横截面面积均为 500 mm2，E=200 GPa。设沿对 角线 AC 方向作用一对 20 kN 的力，试求 A、C 两点的距离改变。 ：(1) 分析铰 A 的受力 B C a A D a 解 A P P NAB NAD NAD NAB 2 2 N N AB AD = = P (2) 分析铰 B 的受力 N’ B AB NBD NBC NBC N’AB NBD ' ' 2 2 2 BC AB BD AB N N N N = = = = P P 同理可得： 2 2 N P CD = (3) 使用功能原理 1 2 W P = δ 2 2 2 2 2 2 222 4 2 2 上海理工大学 力学教研室 9 2 2 i i P a N l P a Pa U EA EA EA EA ⎛ ⎞ ⎜ ⎟ × ⎝ ⎠ × + = =× + = ∑