内蒙古科技大学：《材料力学》课程教学资源（练习题，无答案）应力状态和强度理论

应力状态和强度理论（1）班级学号姓名、选择题（将正确答案填入空格中）1、对于图示各点应力状态，属于单向应力状态的是H02、矩形截面简支梁受力如图a，横截面上各点的应力状态（图b所示）的正确性有（A）点1、2的应力状态是正确的：（B）点2、3的应力状态是正确的；（C）点3、4的应力状态是正确的：（D）点1、5的应力状态是正确的。卓(b)a3、图示梁上a点的应力状态为白4、已知单元体AB、BC面上只作用剪应力T，则AC面上的应力情况光(B) Tuc=号,04e-号r;(A) TAc=号,OAc =0;(D) TAc=-号,c-号P(C) TAc -H,0A计算题（解题要求：①给出坐标方向确定α,T,和α等已知参数；②写出计算公式并代入数据计算；③在图上标出求解结果）1、图示单元体。求：（1）指定斜截面上的应力：（2）主应力大小及主平面方位，并将主平面位置标在单元体图上

应力状态和强度理论（1） 班级 学号 姓名 一、选择题（将正确答案填入空格中） 1、对于图示各点应力状态，属于单向应力状态的是 。 A 20 20 20 20 B C 20 20 20 20 D 20 (MPa) 2、矩形截面简支梁受力如图 a，横截面上各点的应力状态（图 b 所示）的正确性有 。 （A）点 1、2 的应力状态是正确的； （B）点 2、3 的应力状态是正确的； （C）点 3、4 的应力状态是正确的； （D）点 1、5 的应力状态是正确的。 (a) a p 4 5 3 2 1 a p 1 2 (b) 3 4 5 3、图示梁上 a 点的应力状态为 。 a p A B C D 4、已知单元体 AB、BC 面上只作用剪应力  ，则 AC 面上的应力情况为 。 （A） , 0; 2 AC =  AC =   （B） ; 2 3 , 2     AC = AC = （C） ; 2 3 , 2     AC = AC = − （D） . 2 3 , 2     AC = − AC = A τ τ C B 二、计算题（解题要求：①给出坐标方向确定 x y xy  , , 和  等已知参数；②写出计算公 式并代入数据计算；③在图上标出求解结果） 1、图示单元体。求：（1）指定斜截面上的应力；（2）主应力大小及主平面方位，并将主平 面位置标在单元体图上

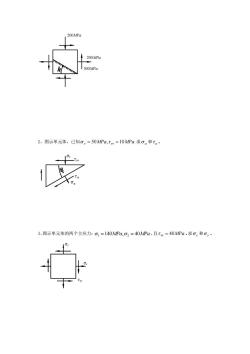
M2、图示单元体，已知,=50MPa,Tx=10MPa.求。和T。。、图示单元体的两个主应力40MPa，且t40MPa。求g.和o，140MPa

300MPa 200MPa 200MPa 2、图示单元体，已知 50MPa, 10MPa.  y =  yx = 求   和   。 σα τα σy τyx 3、图示单元体的两个主应力： 1 =140MPa, 2 = 40MPa ，且  xy = 40MPa 。求  x 和  y 。 τxy σx σy

应力状态和强度理论（2）班级学号生、选择题（将正确答案填入空格中）1、广义虎克定律的适用范围是（A）在屈服极限范围内；（B）在比例极限范围内；（C）在强度极限范围内。2、纯剪切应力状态如图。设α=135°，材料的弹性模量为E，泊松比为μ，则沿n方向的正应力。和线应变6。为(B) 0α=--T,6 =- /E;(A) a=T,ea=/e:(1+μ/(D) 0α=-(1-%(C) 0aT&=T&、填空题1、图示单元体的最大剪应力5题1图题2图2、边长为10mm的正立方体钢块，上方承受P=6KN的压力（均匀分布于面上）。已知v=0.33。1）x、z方向不受约束（图a)。钢块内任意点处的主应力为2)置于刚性槽形模内，两侧面与槽壁无间隙（图b)。钢块内任意点处的主应力为3）置于刚性方形模内，四侧面与模壁无间隙（图c)。钢块内任意点处的主应力为三、计算题1、试求图示各应力状态的主应力及最大剪应力（应力单位为MPa）

应力状态和强度理论（2） 班级 学号 姓名 一、选择题（将正确答案填入空格中） 1、广义虎克定律的适用范围是 。 （A）在屈服极限范围内； （B）在比例极限范围内； （C）在强度极限范围内。 2、纯剪切应力状态如图。设 o  =135 ，材料的弹性模量为 E，泊松比为  ，则沿 n 方向的 正应力   和线应变   为 。 （A） , ; E      =  = （B） , ; E      = −  = − （C） ; (1 ) , E        + = = （D） E (1 ) ,        − = − = 。 n α τ 二、填空题 1、图示单元体的最大剪应力  max = 。 40 50 MPa z (a) x y P (b) (c) P P 题 1 图 题 2 图 2、边长为 10mm 的正立方体钢块，上方承受 P=6KN 的压力（均匀分布于面上）。已知ν=0.33。 1）x、z 方向不受约束（图 a）。钢块内任意点处的主应力为 。 2）置于刚性槽形模内，两侧面与槽壁无间隙（图 b）。钢块内任意点处的主应力为 。 3）置于刚性方形模内，四侧面与模壁无间隙（图 c）。钢块内任意点处的主应力为 。 三、计算题 1、试求图示各应力状态的主应力及最大剪应力（应力单位为 MPa）。 (a) 50 50

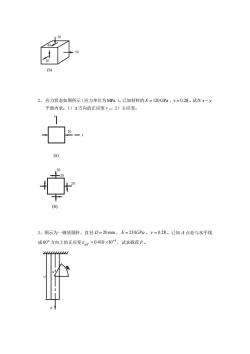
(b)2、应力状态如图所示（应力单位为MPa）。已知材料的E=120GPa，V=0.28。试在x-y平面内求：1）x方向的正应变εx。2）主应变(a)3、图示为一钢质圆杆，直径D=20mm，E=210GPa，V=0.28。已知A点处与水平线成60°方向上的正应变6o=0.410×10，试求载荷P。B

20 (b) 30 40 50 2、 应力状态如图所示（应力单位为 MPa ）。已知材料的 E = 120 GPa ，v = 0.28 。试在 x − y 平面内求：1） x 方向的正应变εx。2）主应变。 (a) y 20 x (b) 30 20 20 3、图示为一钢质圆杆，直径 D = 20 mm ， E = 210GPa ， = 0.28 。已知 A 点处与水平线 成 60 方向上的正应变 3 600 0.410 10−  =  ，试求载荷 P 。 P L A

应力状态和强度理论（3）班级学号姓名一、选择题（将正确答案填入空格中）1、两危险点的应力状态如图，且α=T，由第四强度理论比较其危险程度有下列结轮（A）（a）应力状态危险；(B）（b）应力状态危险；(C)两者的危险程度相同：（D）不能判断。题1图题2图2、图示单元体的应力状态，按第三、第四强度理论的相当应力6,3Or4（C)0.5/7o:（D) 0.5/5g。(A) 1.50 :(B)2g:二、填空题：1、用第四强度理论校核图示点的强度时，MO(oz1)题2图题1图2、图示应力状态，按第三强度理论的强度条件为三、计算题1、对下列给定应力状态确定材料是否失效。（a）对脆性材料按最大拉应力理论，已知材料的,=300Mpa；（b）对塑性材料按最大剪应力理论和形状改变比能理论，已知材料的C,=500Mpa。1),=211MPa，,=-212MPa，T,=212Mpa,脆性材料。2)0,=87MPa,0,=-87MPa,=200MPa,T,=50Mpa,塑性材料

应力状态和强度理论（3） 班级 学号 姓名 一、选择题（将正确答案填入空格中） 1、两危险点的应力状态如图，且  = ，由第四强度理论比较其危险程度有下列结 论 。 （A） （a）应力状态危险； （B） （b）应力状态危险； （C） 两者的危险程度相同； （D） 不能判断。 题1图 τ (a) σ τ (b) σ τ 题2图 σ 2 =σ 2、图示单元体的应力状态，按第三、第四强度理论的相当应力  r3 = ， r4 = 。 （A） 1.5 ； （B） 2 ； （C） 0.5 7 ； （D） 0.5 5 。 二、填空题： 1、用第四强度理论校核图示点的强度时，其相当应力  r4 = 。 题1图 题2图 τxy σx ( > ) σ τxy z τxy σz 2、图示应力状态，按第三强度理论的强度条件为 。 三、计算题 1、对下列给定应力状态确定材料是否失效。（a）对脆性材料按最大拉应力理论，已知材料 的  b =300Mpa；（b）对塑性材料按最大剪应力理论和形状改变比能理论，已知材料的  s =500Mpa。 1）  x = 211 MPa， y = −212 MPa， xy = 212 Mpa，脆性材料。 2）  x = 87 MPa， y = −87 MPa， z = 200 MPa， xy = 50 Mpa，塑性材料

2、从某铸铁构件内的危险点处取出的单元体，其各面上的应力分量如图所示。已知铸铁材料的模向变形系数V=0.25，许用拉应力[o,]=30MPa，许用压应力[。]=90MPa。试按第一和第二强度理论校核其强度。3、用Q235钢制成的实心圆截面杆，受轴向拉力P及扭转力偶矩m共同作用，且m=Pd/10。今测得圆杆表面k点处沿图示方向的线应变3g=57.33×10-。已知该杆直径d=10mm，材料的弹性常数为E=200GPa，V=0.3。试求荷载p和m。若其许用应力[o]=160MPa，试按第四强度理论校核该杆的强度

2、从某铸铁构件内的危险点处取出的单元体，其各面上的应力分量如图所示。已知铸铁材 料的横向变形系数  = 0.25 ，许用拉应力 [ ] = 30MPa  t ，许用压应力 [ ] = 90MPa  c 。试 按第一和第二强度理论校核其强度。 15 (MPa) 15 3、用 Q235 钢制成的实心圆截面杆，受轴向拉力 P 及扭转力偶矩 m 共同作用，且 m = Pd /10。 今测得圆杆表面 k 点处沿图示方向的线应变 5 30 57.33 10−   =  。已知该杆直径 d=10mm，材 料的弹性常数为 E=200GPa， = 0.3 。试求荷载 p 和 m。若其许用应力 [ ] = 160MPa ，试 按第四强度理论校核该杆的强度。 d k m P k

应力状态和强度理论（4）班级学号姓名一、填空题（将正确答案填入空格中）1、梁的受力情况如图所示，画出梁上A、B、C、D点的单元体受力图。目BCD-YL岁2、一般情况下，材料的塑性破坏可选用强度理论；而材料的脆性破坏则选用强度理论。（写出强度理论的具体名称)二、计算题1、已知应力状态如图所示，要求：（1）试用解析法（代公式）求指定截面（标有阴影线者上的应力：（2）用作图法（应力圆法）校核。1 40MPa20M2、某圆柱形薄壁容器的直径为400mm，壁厚为4mm，E=200GPa，泊松比v=0.3，若在与x轴成α=45°方向测得正应变为350×10-，试求：1）最大表面正应变。2）容器壁中的最大正应力。3）容器的内压力由阳上

应力状态和强度理论（4） 班级 学号 姓名 一、填空题（将正确答案填入空格中） 1、 梁的受力情况如图所示，画出梁上 A、B、C、D 点的单元体受力图。 A a C a B L D A B C D 2、一般情况下，材料的塑性破坏可选用 强度理论； 而材料的脆性破坏则选用 强度理论。（写出 强度理论的具体名称） 二、计算题 1、 已知应力状态如图所示，要求：（1）试用解析法（代公式）求指定截面（标有阴影线者） 上的应力；（2）用作图法（应力圆法）校核。 20MPa 40MPa 2、某圆柱形薄壁容器的直径为 400mm，壁厚为 4mm，E = 200GPa ，泊松比  = 0.3 ，若在 与 x 轴成 o  = 45 方向测得正应变为 6 350 10−  ，试求： 1）最大表面正应变。2）容器壁中的最大正应力。3）容器的内压力 电阻片 α x

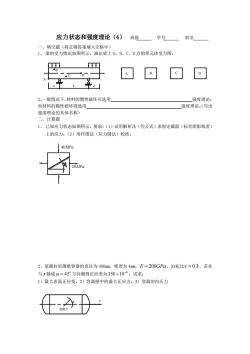
3、从低碳钢零件中某点处取出一单元体，其应力状态如图所示，试按第三、第四强度理论计算单元体的相当应力。单元体上的应力（单位：MPa）为1) 0= 40,0a+90= 40,T。= 60; 2) 0α= 60,0a0p = -80,ta = -40 4、设有单元体如图所示，已知材料的许用拉应力为[o,]=60MPa，许用压应力为[o.]=180MPa。试按莫尔强度理论作强度校核。JM70MP

3、从低碳钢零件中某点处取出一单元体，其应力状态如图所示，试按第三、第四强度理论 计算单元体的相当应力。单元体上的应力（单位：MPa）为 1） 40, 0 40, 60 90 = = =  +     ；2） 60, 0 80, 40 90 = = − = −  +     。 σ τ α α σ+90° τα+90° α 4、设有单元体如图所示，已知材料的许用拉应力为 [ ] = 60MPa  t ，许用压应力为 [ ] = 180MPa  c 。试按莫尔强度理论作强度校核。 50MPa 70MPa