内蒙古科技大学：《材料力学》课程教学资源（习题解答）扭转

3-1.用截面法求图示各杆在截面1-1、2-2、3-3上的扭矩。并于截面上有矢量表示扭矩，指出扭矩的符号。作出各杆扭矩图，(b) 解：（a(）用截面法求1-1截面上的扭矩2kN.m JC-2+T, =0Em,=0..T=2kN.m(2）用截面法求2-2截面上的扭矩Tm,=0-2-T,=0:.T, =-2 kN.m(3）画扭矩图2kN.mD(1）用截面法求1-1截面上的扭矩Zm,=0 -T-5+3-2=0.T, = -4 kN.m(2）用截面法求2-2截面上的扭矩T2

3-1. 用截面法求图示各杆在截面 1-1、2-2、3-3 上的扭矩。并于截面上有矢量表示扭矩，指 出扭矩的符号。作出各杆扭矩图。 (b) 5kN.m 3kN.m 2kN.m 1 1 2 2 3 3 2kN.m 1 (a) 4kN.m 2kN.m 1 2 2 解: (a) (1) 用截面法求 1-1 截面上的扭矩 2kN.m 1 1 T1 x 1 1 0 2 0 2 . m T x T kN m = −+ = ∴ = ∑ (2) 用截面法求 2-2 截面上的扭矩 2 2kN.m 2 T2 x 2 2 0 2 0 2 . m T x T kN m = −− = ∴ =− ∑ (3) 画扭矩图 T x 2kN.m 2kN.m (b) (1) 用截面法求 1-1 截面上的扭矩 5kN.m 3kN.m 2kN.m 1 1 T1 x 1 1 0 5 3 2 0 4 . m T x T kN m = − −+−= ∴ =− ∑ (2) 用截面法求 2-2 截面上的扭矩 2 3kN.m 2kN.m 2 T2 x

Zm =0 -T,+3-2=0..T, =1 kNm(3）用截面法求3-3截面上的扭矩Zm,=0-T,-2=0..T, =-2 kN.m(4)画扭矩图KN.2kN.m3.3.直径D=50mm的圆轴受扭矩T=2.15kN.m的作用。试求距轴心10mm处的切应力，并求横截面上的最大切应力。解：（1）圆轴的极惯性矩I-3200%=614×10 m3232点的切应力TP_2.15x10x0.01=35.0MPa6.14×10-71(2）圆轴的抗扭截面系数_614x10=2.456×10~ mW.-DT2~0.052截面上的最大切应力T2.15×103= 87.5 MPaTmaxw,2.456x10-5注：截面上的切应力成线性分布，所以也可以用比例关系求最大切应力。D/2-35.0 005/2=87.5 MPaTmax =t)0.013.4.发电量为1500kW的水轮机主轴如图示。D=550mm，d-300mm，正常转速n=250r/min。材料的许用剪应力[t]=500MPa。试校核水轮机主轴的强度上海理工大学力学教研室

2 2 0 3 2 0 1 . m T x T kN m = − +−= ∴ = ∑ (3) 用截面法求 3-3 截面上的扭矩 3 3 0 2 0 2 . m T x T kN m = − −= ∴ =− ∑ 3 2kN.m 3 T3 x (4) 画扭矩图 T x 1kN.m 2kN.m 4kN.m 3.3. 直径 D=50 mm 的圆轴受扭矩 T=2.15 kN.m 的作用。试求距轴心 10 mm 处的切应力，并 求横截面上的最大切应力。 解: (1) 圆轴的极惯性矩 4 4 32 0.05 7 4 6.14 10 32 32 P D I m π × − = = =× 点的切应力 3 7 2.15 10 0.01 35.0 6.14 10 p T MPa I ρ τ − × × = = = × (2) 圆轴的抗扭截面系数 7 6.14 10 5 3 2.456 10 / 2 0.05/ 2 p t I W m D − × − == =× 截面上的最大切应力 3 max 5 2.15 10 87.5 2.456 10 t T MPa W τ − × == = × 注：截面上的切应力成线性分布，所以也可以用比例关系求最大切应力。 max / 2 0.05/ 2 35.0 87.5 0.01 D τ τ MPa ρ =× = × = 3.4. 发电量为 1500 kW 的水轮机主轴如图示。D=550 mm，d=300 mm，正常转速 n=250 r/min。 材料的许用剪应力[τ]=500 MPa。试校核水轮机主轴的强度。 上海理工大学 力学教研室 1

t轮利解：（1）计算外力偶矩1500 = 57.29 kN.mm=9549_=9549x250(2)计算扭矩T = m= 57.29 kN.m(3）计算抗扭截面系数(Dt- d*)=29.8x10-3 mW =161(4）强度校核T57.29×103=19.2MPa <[α]T=W=29.8x10强度足够。注：强度校核类问题，最后必需给出结论。3-5.图示轴AB的转速i=120T/min，从B轮输入功率P=4.1kW，功率的一半通过锥形齿轮传送给轴C，另一半由水平轴H输出。已知D-60 cm,D=-24cm，dl=10 cm,d=8cm，d=6cm，[tl-20MPa。试对各轴进行强度校核。akI解：（1）计算外力偶矩x44.1 =3509 N.mP=9549m= 9549.120Im=1755 N.mmu=44.1R=9549-= 701.9 N.mmc= 9549D8 120DixnD上海理工大学力学教研室

d D 发电机轴 水轮机轴 解：(1) 计算外力偶矩 1500 9549 9549 57.29 . 250 P m k n = =×= N m (2) 计算扭矩 T m kN m = = 57.29 . (3) 计算抗扭截面系数 4 4 3 ( ) 29.8 10 16 W Dd t D 3 m π − = −= × (4) 强度校核 3 3 57.29 10 19.2 [ ] 29.8 10 t T MPa W τ σ − × == = × ≺ 强度足够。 注：强度校核类问题，最后必需给出结论。 3-5. 图示轴AB的转速n=120 r/min，从B轮输入功率P=44.1 kW，功率的一半通过锥形齿轮传 送给轴C，另一半由水平轴H输出。已知D1=60 cm，D2=24 cm，d1=10 cm，d2=8 cm，d3=6 cm，[τ]=20 MPa。试对各轴进行强度校核。 d2 d1 d3 D1 D2 H A B C 解：（1）计算外力偶矩 1 2 44.1 9549 9549 3509 . 120 1 1755 . 2 44.1 2 2 9549 9549 701.9 . 60 120 24 H C P m N n m m Nm P m N D n D = =×= = = == = × × m m 上海理工大学 力学教研室 2

（2）计算内力扭矩Tas=m=3509N.mTh=mz=1755NmT = mc = 701.9N.m（3）计算抗扭截面系数Wun==×0. P=196×10~ mWa=4×0.08=10010~mWc--×0.06=42.4x10-m（4）强度校核3509T=17.9MPa<[t]TABmWuB"196x10-1755IL=17.55MPa[]HmayW.100×10-6A701.9= 16.55 MPa [1]tcmaxWic42.4×10%c强度足够。3-6.图示阶梯形圆轴直径分别为d=40mm，d=70mm，轴上装有三个带轮。已知由轮3输入的功率为P;=30kW，轮1输出的功率为P,=13kW，轴作匀速转动，转速n=200r/min材料的许用剪应力[t}-60 MPa,G=80 GPa，许用扭转角[9]-2%m。试校核轴的强度和冈度。C.dco0.5m 10.3ml解：（1）计算外力偶矩m =9549号-9549×20013=620.7Nmm =9549 =9549× 30=1432.4Nm200(2)计算扭矩T, =-m =-620.7 N.m=-m=-1432.4N.mTIkN.n620.7N.m432.47上海理工大学力学教研室

（2）计算内力扭矩 3509 . 1755 701.9 . AB H H C C T m Nm T m N T m Nm = = = = = = m （3）计算抗扭截面系数 33 6 1 3 36 2 3 3 3 0.1 196 10 16 16 0.08 100 10 16 16 0.06 42.4 10 16 16 tAB tH tC W d m W d W d 3 3 6 3 m m π π π π π π − − − = =× = × = =× = × = =× = × （4）强度校核 max 6 max 6 max 6 3509 17.9 [ ] 196 10 1755 17.55 [ ] 100 10 701.9 16.55 [ ] 42.4 10 AB AB tAB H H tH C C tC tC T MPa W T MPa W T MPa W τ τ τ τ τ τ − − − == = × == = × == = × ≺ ≺ ≺ 强度足够。 3-6. 图示阶梯形圆轴直径分别为d1=40 mm，d2=70 mm，轴上装有三个带轮。已知由轮 3 输 入的功率为P3=30 kW，轮 1 输出的功率为P1=13 kW，轴作匀速转动，转速n=200 r/min， 材料的许用剪应力[τ]=60 MPa，G=80 GPa，许用扭转角[θ]=2 o /m。试校核轴的强度和刚 度。 m2 m3 解：(1) 计算外力偶矩 1 1 3 3 13 9549 9549 620.7 200 30 9549 9549 1432.4 200 P m N n P m N n = = ×= = = ×= m m (2) 计算扭矩 12 1 23 3 T m Nm T m Nm =− =−620.7 . =− =−1432.4 . m1 A 1 C B 2 3 0.5m 1m D d2 d1 0.3m T x 1kN.m 1432.4N.m 620.7N.m 上海理工大学 力学教研室 3

(3）计算抗扭截面系数元×0.043=12.56×10-mWa=d=Wa-"d,--元×0.073=67.31×10~m(4)强度校核620.7112 1. 5010-4.42MPa[] Tmax1 =1432.4T23 =21.28MPa≤[] Tmax2 =w,z67.31x10-6强度足够。5）计算截面极惯性矩 =12.56×10~×0.04Ipr=W,x4= 25.12×10-8 m=67.31×1023.56×107mIn=W,x2(6)刚度校核T2180°620.7180° =1.77° / m [0]Omaxl= Gl,80×10°×25.12×10-8元元1432.4T2s180°x180° =0.435 m [0]0max2=元80×10°×23.56×10-7×GIp2刚度足够。注：本题中扭矩的符号为负，而在强度和刚度计算中，扭矩用其数值代入。3.9，实心轴和空心轴由牙嵌式离合器连接在一起，如图所示。已知轴的转速为n=100r/min传递的功率P=7.5kW，材料的许用剪应力[t]=40MPa。试选择实心轴直径d;和内外径比值为1/2的空心轴外径D2。--解：（1）计算外力偶矩x75=716.2N.mm=9549=9549x100(2)计算内力-扭矩T = m= 716.2N.m(3）计算抗扭截面系数上海理工大学力学教研室

(3) 计算抗扭截面系数 3 3 1 1 3 3 2 2 0.04 12.56 10 16 16 0.07 67.31 10 16 16 t t W d W d 6 3 6 3 m m π π π π − − = =× = × = =× = × (4) 强度校核 [ ] [ ] 12 max1 6 1 23 max 2 6 2 620.7 49.42 12.56 10 1432.4 21.28 67.31 10 t t T MPa W T MPa W τ τ τ τ − − == = ≤ × == = ≤ × 强度足够。 (5) 计算截面极惯性矩 1 6 8 1 1 2 6 7 2 2 0.04 12.56 10 25.12 10 2 2 0.07 67.31 10 23.56 10 2 2 p t p t d 4 3 I W m d I W m − − − − = ×= × × = × = ×= × × = × (6) 刚度校核 12 max1 9 8 1 23 max 2 9 7 2 180 620.7 180 1.77 / [ ] 80 10 25.12 10 180 1432.4 180 0.435 / [ ] 80 10 23.56 10 o o o p o o o p T m GI T m GI θ θ π π θ θ π π − − =×= × = ×× × =×= × = ×× × ≺ ≺ 刚度足够。 注：本题中扭矩的符号为负，而在强度和刚度计算中，扭矩用其数值代入。 3.9. 实心轴和空心轴由牙嵌式离合器连接在一起，如图所示。已知轴的转速为n=100 r/min， 传递的功率P=7.5 kW，材料的许用剪应力[τ]=40 MPa。试选择实心轴直径d1和内外径 比值为 1/2 的空心轴外径D2。 D2 d2 d1 解：(1) 计算外力偶矩 7.5 9549 9549 716.2 . 100 P m N n = = ×= m (2) 计算内力-扭矩 T m Nm = = 716.2 . (3) 计算抗扭截面系数 上海理工大学 力学教研室 4

Wa-idW,-D(1-α) (4)设计截面oa-16T16×716.2D, ==46mmV元[（1-α）元×40×10%1-0.5）注：也可以用比例关系求直径D2。d.45=-D, == 46 mm/1-α4/1-0.543.11.图示传动轴的转速为n=500r/min，主动轮1输入功率P-=368kW，从动轮2、3分别输出功率P,=147kW,P,=221 kW。已知[t}]-70 MPa,[9]-1 %m，G=80 GPa。（）确定AB段的直径d和BC段的直径d2；(2）若AB和BC两段选用同一直径，试确定其数值(3）主动轮和从动轮的位置如可以重新安排，试问怎样安置才比较合理？解：(1)计算外力偶矩m =9549=9549×28=7028 Nm500m=9549号-9549 -2807Nm500m 954号- 9549 2-421 m500(2)计算内力-扭矩Tz =-m, =-7028 N.mT2, =-m, =-4221N.m上海理工大学力学教研室

3 1 1 3 4 2 2 16 1 (1 ) 16 2 t t W d W D π π α α = = − = (4) 设计截面 3 1 3 3 1 6 3 4 2 3 3 2 4 6 4 16 [ ] 16 16 716.2 45 [ ] 40 10 (1 ) 16 [ ] 16 16 716.2 46 [ ](1 ) 40 10 (1 0.5 ) T d T d m T D T D m m m π τ πτ π π α τ πτ α π ≥ × == = × × − ≥ × == = − ×× − 注：也可以用比例关系求直径D2。 1 1 3 4 2 3 43 4 2 45 1 46 1 1 0.5 d d D mm D α α =− = = = − − 3.11. 图示传动轴的转速为n=500 r/min，主动轮 1 输入功率P1=368 kW，从动轮 2、3 分别输 出功率P2=147 kW，P3=221 kW。已知[τ]=70 MPa，[θ]=1 o /m，G=80 GPa。 (1) 确定AB段的直径d1和BC段的直径d2； (2) 若 AB 和 BC 两段选用同一直径，试确定其数值。 (3) 主动轮和从动轮的位置如可以重新安排，试问怎样安置才比较合理？ 1 P 3 A B C P 2 P1 2 3 500 400 解：(1) 计算外力偶矩 1 1 2 2 3 3 368 9549 9549 7028 . 500 147 9549 9549 2807 . 500 221 9549 9549 4221 . 500 P m N n P m N n P m N n = = ×= = = ×= = = ×= m m m m m (2) 计算内力-扭矩 12 1 23 3 7028 . 4221 . Tm N Tm N = − =− =− =− 上海理工大学 力学教研室 5

(3）计算AB段的直径d;和BC段的直径d2根据强度条件设计W=B4[t]16T,16×7028=80mmdV元[t]V元×70×10W.16T16x422 = 67 mmd.≥1-1元x70x10根据刚度条件设计32×7028×18032T,×180= 84.6 mmd≥80×10×元×lVG元'[9]T23×180In=d≥%80474.5mm:d,≥/P(00-180x10综合强度和刚度条件，取d,=84.6mm d,=74.5mm(4)若AB和BC两段选用同一直径，则取d,=d, =84.6mm(5）将A轮和B轮对调位置，则T12=2807N.m，最大扭矩减小，轴的扭转强度提高了所以主动轮放在中间更合理。3.13.设圆轴横截面上的扭矩为T，试求四分之一截面上内力系的合力的大小、方向及作用点。解：（I）取微元dA，上面的切应力是t，则微力为t,dA：Tp-Tp-32TpdA=pdpdpT。元d32上海理工大学力学教研室6

(3) 计算AB段的直径d1和BC段的直径d2 根据强度条件设计 3 12 1 1 12 3 3 1 6 16 [ ] 16 16 7028 80 [ ] 70 10 t T W d T d m π τ πτ π = ≥ × ≥= = × × m 3 23 2 2 23 3 3 2 6 16 [ ] 16 16 4221 67 [ ] 70 10 t T W d T d m π τ πτ π = ≥ × ≥= = × × m 根据刚度条件设计 4 12 1 1 12 4 4 1 2 9 2 180 32 [ ] 32 180 32 7028 180 84.6 [ ] 80 10 1 p T I d G T d m G π θ π π θ π = ≥× × ×× ∴≥ = = × ×× m 4 23 2 2 23 4 4 2 2 9 2 180 32 [ ] 32 180 32 4221 180 74.5 [ ] 80 10 1 p T I d G T d m G π θ π π θ π = ≥× × × × ∴≥ = = × ×× m 综合强度和刚度条件，取 d1 = dmm 2 = 5.74 6.84 mm (4) 若 AB 和 BC 两段选用同一直径，则取 = dd 21 = 6.84 mm (5) 将 A 轮和 B 轮对调位置，则 T12=2807N.m，最大扭矩减小，轴的扭转强度提高了， 所以主动轮放在中间更合理。 3.13. 设圆轴横截面上的扭矩为 T，试求四分之一截面上内力系的合力的大小、方向及作用 点。 O T τρ dρ dϕ ϕ ρ d O T 解：(1) 取微元dA，上面的切应力是τρ，则微力为τρdA： 4 4 32 32 TT T dA d d I d d ρ ρ ρ ρ ρϕρ τ π π = == = 上海理工大学 力学教研室 6

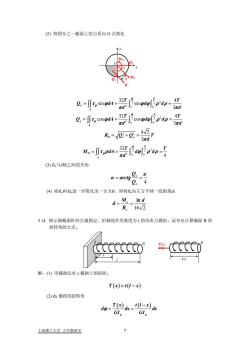
(2）将四分之一截面上的力系向O点简化Ro=N0+0,-Mo f a- -(3) R。与x轴之间的夹角2_元a=arctg80"4(4）将R。和M.进一步简化为一合力R，即将R。向左方平移一段距离d：d=M._3rdR.16V23.14.图示圆截面杆的左端固定，沿轴线作用集度为t的均布力偶矩。试导出计算截面B的扭转角的公式。Ctcero1-x解：（1）用截面法求x截面上的扭矩：T(μ)=t(1-x)(2)dx微段的扭转角T(x) dx:(l-x) dxd=Gl,GI,上海理工大学力学教研室

(2) 将四分之一截面上的力系向 O 点简化 y 2 2 2 4 0 0 2 2 2 4 0 0 2 2 32 4 sin sin 3 32 4 cos cos 3 4 2 3 d x A d y A O xy T T Q dA dd d d T T Q dA dd d d R QQ T d π ρ π ρ τ ϕ ϕϕ ρ ρ π π τ ϕ ϕϕ ρ ρ π π π == = = = = += ∫∫ ∫ ∫ ∫∫ ∫ ∫ = 3 2 2 4 0 0 32 4 d O A T T M dA d d d π ρ τ ρ ϕ ρ ρ π == = ∫∫ ∫ ∫ (3) Ro与x轴之间的夹角 4 π Q Q α arctg x y = = (4) 将Ro和Mo进一步简化为一合力R，即将Ro向左方平移一段距离d： 216 3π d R M d o o == 3.14. 图示圆截面杆的左端固定，沿轴线作用集度为 t 的均布力偶矩。试导出计算截面 B 的 扭转角的公式。 解：(1) 用截面法求 x 截面上的扭矩： Tx tl x ( ) = ( − ) (2) dx 微段的扭转角 ( ) ( ) p p Tx tl x d dx GI GI ϕ − = = dx O MO Qx α x Qy RO d R x l B A B T(x) l-x 上海理工大学 力学教研室 7

(3）截面B的扭转角rut(l-x)dx=t?PBA = J.GI,2GI,3.15.将钻头简化成直径为20mm的圆截面杆，在头部受均布阻抗扭矩t的作用，许用剪应力为[t}=70 MPa，G=80 GPa。(1)求许可的 m；(2)求上、下两端的相对扭转角。解：（I）画扭矩图由扭矩图知T* =- m= .1t(2）确定许可载荷：m=TW[]=[t]×0.02×70×10=110 Nm(3）求上、下两端的相对扭转角：9=10,+1, d-0.2m, (10m)x(0.1P/2)_0.25mGL.GL,GI,0.25x1108010000.22 d =126323.17.AB和CD两轴的B、C两端以凸缘相连接，A、D两端则都是固定端。由于两个凸缘的螺钉孔的中心线未能完全生命形成一个角度为的误差。当两个凸缘由螺钉联接后，试度求两轴的装配扭矩。O:-.解：(1）整体受力分析，列平衡方程：上海理工大学力学教研室

(3) 截面 B 的扭转角 ( ) 2 0 2 l BA p p tl x tl dx GI GI ϕ − = = ∫ 3.15. 将钻头简化成直径为 20mm 的圆截面杆，在头部受均布阻抗扭矩 t 的作用，许用剪应 力为[τ]=70 MPa，G=80 GPa。(1)求许可的 m；(2)求上、下两端的相对扭转角。 100 200 t m T m x 0.1t 解：(1) 画扭矩图 由扭矩图知 max T m= = 0.1t (2) 确定许可载荷： 3 36 max [ ] [ ] 0.02 70 10 110 . 16 16 mT W d t N m π π = ≤ = = × ×× = τ τ (3) 求上、下两端的相对扭转角： ( ) ( ) 0.2 0.1 0 0 2 4 9 0.2 10 0.1 / 2 0.25 0.25 110 0.022 1.26 0.02 80 10 32 p p pp p o m tx dx dx GI GI m m m GI GI GI rad ϕ π = + × =+ = × = = × × × ∫ ∫ = 3.17. AB 和 CD 两轴的 B、C 两端以凸缘相连接，A、D 两端则都是固定端。由于两个凸缘 的螺钉孔的中心线未能完全生命形成一个角度为的误差。当两个凸缘由螺钉联接后， 试度求两轴的装配扭矩。 A B C D a b GIp1 GIp2 ψ mA MD 解：(1) 整体受力分析，列平衡方程： 上海理工大学 力学教研室 8

mp-m,=0这是一次静不定问题。(2)求 AB、CD 杆内的扭矩Tas=m, To=mp(3)AB、CD 杆扭转变形Tob=mpbTABamAau"Gin"GnOo"Cfn"GJn(4)变形几何关系Pns + cn =yma+mb=yG,IprG,Ip2(5)解联方程组VG,G,,p2m,-m,=Ta=To=aG1g*bo1,3.19.图示结构中，AB和CD两杆的尺寸相同。AB为钢杆，CD为铝杆，两种材料的切变模量之比为G钢:G=3:1。若不计BE和ED两杆的变形，试问P将以怎样的比例分配于AB和CD杆上。解：（1）解除E处约束，受力分析R本题为扭转一次静不定问题(2)计算杆的扭转角AB:(R'sa)LABPARGal,上海理工大学力学教研室

0 m m D A − = 这是一次静不定问题。 (2) 求 AB、CD 杆内的扭矩 Tm Tm AB A CD = = D (3) AB、CD 杆扭转变形 11 11 2 2 2 2 AB A CD D BA CD P P P T a ma T b m b GI GI GI GI ϕ ϕ == = = P (4) 变形几何关系 11 2 2 BA CD A D P P ma mb GI GI ϕ ϕ ψ ψ + = + = (5) 解联方程组 12 1 2 2 2 11 = p p A D AB CD p p GG I I mm T T aG I bG I ψ === + 3.19. 图示结构中，AB和CD两杆的尺寸相同。AB为钢杆，CD为铝杆，两种材料的切变模量 之比为G钢:G铝=3:1。若不计BE和ED两杆的变形，试问P将以怎样的比例分配于AB和CD 杆上。 解：(1) 解除 E 处约束，受力分析 P C D B A a a E P C D B A E E RE R’E 本题为扭转一次静不定问题 (2) 计算杆的扭转角 AB： ( ' E ) AB AB AB p R a L G I ϕ = 上海理工大学 力学教研室 9