内蒙古科技大学：《材料力学》课程教学资源（习题辅导）能量方法

50第十一章能量法第十一章能量方法11.1图示桁架各杆的材料相同，截面面积相等。试求在F力作用下，桁架的变形能。2FNI = FN2E2FL2Fr(x)J2EA2EA2EA3F224EA11.2计算图示各杆的应变能。MeEI24A1321/3xx2(a)(b)MllMllF1,F213F21(a) V. 2EA 4EA 4EAM.13:11/3（(b) V,=[dx+dx2EI2EIMM((x)+32E18EI

50 第十一章 能量法 1 A l l l B F 2 3 第十一章 能量方法 11.1 图示桁架各杆的材料相同，截面面积相等。试求在 F 力作用下，桁架的 变形能。 1 2 2 , 2 F F F N N = = 3 2 N F F = 2 2 2 2 2 2 2 ( ) 2 2 2 2 2 N F F l l F x V dx EA EA EA              = = +  2 2 3 4 F l EA = . 11.2 计算图示各杆的应变能。 (a) 2 2 2 3 2 4 4 F l F l F l V EA EA EA  = + = . (b) 2 2 1 2 /3 2 /3 1 2 0 0 2 2 e e l l M M x x l l V dx dx EI EI              = +   /3 2 /3 2 2 2 2 1 2 2 0 0 2 3 3 18 l l M M l e e x x EIl EI       = + =               . Me 2A l l A F EI (a) B C A B C A l/3 2l/3 (b) x2 Me/l Me 2A l l A F EI (a) B C A B C A l/3 2l/3 (b) Me 2A l l A F EI (a) B C A B C A l/3 2l/3 (b) Me 2A l l A F EI (a) B C A B C A l/3 2l/3 M (b) e/l Me 2A l l A F EI (a) B C A B C A l/3 2l/3 (b) x1 Me/l Me 2A l l A F EI (a) B C A B C A l/3 2l/3 (b) x1 Me/l Me 2A l l A F EI (a) B C A B C A l/3 2l/3 (b) Me/l Me 2A l l A F EI (a) B C A B C A l/3 2l/3 (b) Me/l Me 2A l l A F EI (a) B C A B C A l/3 2l/3 (b)

第十一章能量法5111.3传动轴受力情况如图所示。轴的直径为40mm，材料为45钢，E=210GPa，G=80GPa。试计算轴的应变能。0.36kN1kN由扭转引起的应变能：4r0.2802200-200-Va=1"2G1,dx = 0.032由弯曲引起的应变能：(p-2 6314) x= .029Vt = 2 /。2EI扭矩图80N-mV, =V.I+Ve2 =0.061J.田弯矩图11.4计算图示梁的应变能，并说明是否满足531.4Nm叠加原理及其原因。Me-FFF213-IaAEI6EI2EIx而F213-2EIFP-"Fu dxVea=J.2EI6EI不满足叠加原理，因为应变能与内力的关系不是线性的

第十一章 能量法 51 11.3 传动轴受力情况如图所示。轴的直径为 40mm，材料为 45 钢，E = 210GPa， G = 80GPa。试计算轴的应变能。 由扭转引起的应变能： 2 0.2 2 0 80 0.032 2 p V dx GI  = =  由弯曲引起的应变能： 2 0.2 1 0 (531.4 ) 2 0.029 2 x V dx EI  = =  1 2 V V V 0.061J    = + = . 11.4 计算图示梁的应变能，并说明是否满足 叠加原理及其原因。 2 2 3 0 ( ) 2 6 l Fl Fx F l V dx EI EI  − = =  而 2 2 3 1 0 ( ) 2 2 l Fl F l V dx EI EI  = =  2 2 3 2 0 ( ) 2 6 l Fx F l V dx EI EI  − = =  . 不满足叠加原理，因为应变能与内力的关系不是线性的。 0.08kN·m 0.36kN (b) 1kN 200 0 200 EI Me=Fl F l x

52第十一章能量法115在外伸梁的自由端作用力偶矩M，试用互等定理，并借助于附录M1跨度中点C的挠度we。常B -1/2（见课本下册p40例12-4）11.6图示刚架的各杆的EI皆相等，试求截面A、B的位移和截面C的转角。111124x3kx2/c5(a(a)A点：在A点加一个向下的单位力。M(x1)=0,M(x2)=Fx2,M(x3)=FbFabh M(s)M() d, =-M(x)=x, M(cg)=Fx, M(s)=0 A=J。EIEIC点：在C加一个逆时针的力偶矩为1的单位力偶。M(xs)=1，M(s)=1 M(rM(ds ++Md2EFb2,FbhA=J0EIEI()4点：在4点加一个向下的单位力。M()=号x-等,M()一*S)cl222-5ql2△=2f°Ldx:EI384EIB点：在B点加一个向右的单位力。M(x)=hh(gx_gr)ql'hA=J。dx=EI12EI

52 第十一章 能量法 11.5 在外伸梁的自由端作用力偶矩 Me，试用互等定理，并借助于附录 E，求 跨度中点 C 的挠度 wc。 （见课本下册 p40 例 12-4） 11.6 图示刚架的各杆的 EI 皆相等，试求截面 A、B 的位移和截面 C 的转角。 (a) A 点：在 A 点加一个向下的单位力。M(x1)=0, M(x2)=Fx2, M(x3)=Fb 1 1 M x x ( ) = , 2 2 M x Fx ( ) = , 3 M x( ) 0 = 3 3 3 0 h M x M x ( ) ( ) Fabh dx EI EI  = = −  . C 点：在 C 加一个逆时针的力偶矩为１的单位力偶。 2 M x( ) 1 = , 3 M x( ) 1 = 2 2 3 3 2 3 0 0 b h M x M x ( ) ( ) M x M x ( ) ( ) dx dx EI EI  = +   2 2 Fb Fbh EI EI = + . (b) A 点：在 A 点加一个向下的单位力。 2 ( ) 2 2 ql qx M x x = − , 1 ( ) 2 M x x = 2 4 / 2 0 1 2 2 2 5 2 384 l qlx qx x ql dx EI EI     −    = =  . B 点：在 B 点加一个向右的单位力。 M x h ( ) = 2 3 0 ( ) 2 2 12 l qlx qx h ql h dx EI EI −  = =  . C Me A l/2 l/2 B D a A F a C b C h (a) A l h B (b) q l/2 C A x2 F a C b C h (a) A l h B (b) q l/2 C x3 x x1

第十一章能量法53 11.7图示桁架各杆的材料相同，截面面积相等。试求节点C处的水平位移和2F垂直位移。FB杆号2453F0FN-N2FFF水平-1000N2F垂直0。-100V2AD水平位移：A-2MMR台EAA122H_FIEAEA(1+2/2)FI-_3.828FIEAEA垂直位移：FI4=-EA11.8图中绕过无摩擦滑轮的钢索的截面面积为76.36mm2，E索=177GPa。F=20kN，（a）假设横梁ABCD为刚体，求C点的垂直位移。(2）若不把ABCD假设为刚体，且已知其抗弯刚度为EI=1440kN.m2，试再求C点的垂直位移。?() 4=(F/×0.87.89×10m.ALB/60°60ALAFx?c(2)=7.89×10+2/dEI=7.89×10-+1.48×10= 9.37×10-m.1/V3AA

第十一章 能量法 53 11.7 图示桁架各杆的材料相同，截面面积相等。试求节点 C 处的水平位移和 垂直位移。 杆号 1 2 3 4 5 FN F -F - 2 F F 0 FN 水平 0 0 2 -1 0 FN 垂直 0 0 0 -1 0 l l l 2 l l l 水平位移： 1 2 2 n Ni Ni i i F F l EA Fl Fl EA EA =  = = − −  (1 2 2) 3.828 Fl Fl EA EA + = − = − . 垂直位移： Fl EA  = − . 11.8 图中绕过无摩擦滑轮的钢索的截面面积为 76.36mm2，E 索 = 177GPa。F = 20kN，(a) 假设横梁 ABCD 为刚体，求 C 点的垂直位移。(2) 若不把 ABCD 假 设为刚体，且已知其抗弯刚度为 EI = 1440kN.m2，试再求 C 点的垂直位移。 (1) 2 1 1 4 0.8 7.89 10 3 3 F EA   −  =  =      m. (2) 2 0.4 4 0 4 7.89 10 2 Fx dx EI −  =  +  4 4 4 7.89 10 1.48 10 9.37 10 − − − =  +  =  m. 2F B C A D F l l D C F A B 60° 60° 800 400 400

54第十一章能量法11.9等截面曲杆BC的轴线为四分之三的圆周。若AB杆可视为刚性杆，试求在F力作用下，截面B的水平位移及垂直位移。水平位移：M0)=FRcose,M(0)=RsinFRsinocosdo=FRA=EI2EI垂直位移：M(O)=-R(1-cosO)[FR cos01-cos0) o 4+3m)FRAEI4EI?3.36FR3EI11.10图示圆弧形小曲率杆，平均半径为R。力F垂直于圆环中线所在的平面。试求两个F力作用点的相对线位移。M(0)=FRsine, M(0)=RsinT(0=FR(1-cos0), T(0)=R(1-cos0)TAB+FA- R's- r"=FR*(L-cos0) oEGI,元FR3元FR3EIGl

54 第十一章 能量法 C F B A R B F O R A F 11.9 等截面曲杆 BC 的轴线为四分之三的圆周。若 AB 杆可视为刚性杆，试求 在 F 力作用下，截面 B 的水平位移及垂直位移。 水平位移：M()=FRcos, M R ( ) sin   = 3 3 3 2 0 sin cos 2 FR FR d EI EI     = =   . 垂直位移： M R ( ) (1 cos )   = − − 3 3 3 2 0 cos (1 cos ) (4 3 ) 4 FR FR d EI EI      − +  = =  3 3.36FR EI = . 11.10 图示圆弧形小曲率杆，平均半径为 R。力 F 垂直于圆环中线所在的平面。 试求两个 F 力作用点的相对线位移。 M()=FRsin, M R ( ) sin   = T()=FR(1-cos), T R ( ) (1 cos )   = − 3 2 3 2 2 2 0 0 sin (1 cos ) p FR FR d d EI GI       −  = +   3 3 3 p FR FR EI GI   = +

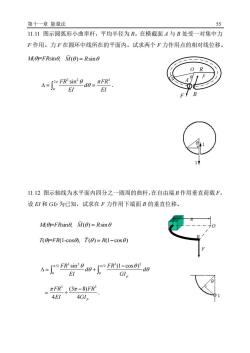
第十一章能量法5511.11图示圆弧形小曲率杆，平均半径为R。在横截面A与B处受一对集中力F作用。力F在圆环中线所在的平面内。试求两个F力作用点的相对线位移M(0)-FRsing, M(0)=RsingA-I"FRsr- do FREIEIR1t11.12图示轴线为水平面内四分之一圆周的曲杆，在自由端B作用垂直荷载F，设EI和GIp为已知，试求在F力作用下端面B的垂直位移。M(0)-FRsine, M()=RsinT(0)=FR(1-cos), T(0)= R(1-cos0)-adEIGI,元FR*（3元-8)FR34EI4GIp

第十一章 能量法 55 R F O B 11.11 图示圆弧形小曲率杆，平均半径为 R。在横截面 A 与 B 处受一对集中力 F 作用。力 F 在圆环中线所在的平面内。试求两个 F 力作用点的相对线位移。 M()=FRsin, M R ( ) sin   = 3 2 3 2 0 FR FR sin d EI EI     = =   . 11.12 图示轴线为水平面内四分之一圆周的曲杆，在自由端 B 作用垂直荷载 F， 设 EI 和 GIP 为已知，试求在 F 力作用下端面 B 的垂直位移。 M()=FRsin, M R ( ) sin   = T()=FR(1-cos), T R ( ) (1 cos )   = − 3 2 3 2 / 2 / 2 0 0 sin (1 cos ) p FR FR d d EI GI       −  = +   3 3 (3 8) 4 4 p FR FR EI GI   − = + . F O O O R θ F B A