内蒙古科技大学：《材料力学》课程教学资源（习题解答）组合变形

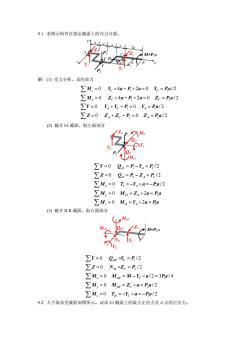
9.1.求图示构件在指定截面上的内力分量27IPM=P解：（1）受力分析，求约束力ZM,=0Y.x4a--P×2a=0Y.=Pa/2ZM,=0Z×4a-P×2a=0 Zc=Pa/2ZY=0Y+Yc-P=0Y=Pa/2Zz=0Z,+Zc-P,=0 Z,=Pa/2(2）截开I-I截面，取左面部分2,,=P-Y=P/2ZY=0Zz=0Qu=P,-Z,=P, /2ZM,=0 T,=-Y,xa=-Pa/2ZM,=0 My=Z,×2a=PaZM,=0M,=Y,×2a= Pa(3）截开I-II截面，取右面部分loylMxllZY=0Q =Y= P /2Zz=0N=Zc=P,/2ZM,=0 M=M-Yxa/2=3Pa/4ZM,=0 Mm=Zexa=P,a/2ZM,=0 Tu=-Yxa=-Pa/29.2.人字架承受载荷如图所示。试求1-I截面上的最大正应力及4点的正应力

9.1. 求图示构件在指定截面上的内力分量。 z x y a a a a 2a P2 P1 M=P1a II II I I a/2 a A B C YA YC ZC ZA 解：(1) 受力分析，求约束力 1 1 2 2 1 1 2 2 0 4 2 0 / 2 0 4 2 0 / 2 0 0 / 2 0 0 / 2 z C C y C C A C A A C A M Y a P a Y Pa M Z a P a Z Pa Y Y Y P Y Pa Z Z Z P Z Pa = × −× = = = ×−× = = = + −= = = + −= = ∑ ∑ ∑ ∑ (2) 截开 I-I 截面，取左面部分 1 1 2 2 1 2 1 0 / 2 0 / 2 0 / 2 0 2 0 2 y I A zI A x IA y yI A z zI A Y Q PY P Z Q PZ P M T Y a Pa M M Z aP M M Y a Pa = =− = = =− = = =− × =− = = ×= = =×= ∑ ∑ ∑ ∑ ∑ P2 P1 YA ZA QzI QyI TI MzI MyI a (3) 截开 II-II 截面，取右面部分 M=P1a YC QyII ZC NII MxII TII MyII 1 2 1 2 1 0 / 2 0 / 2 0 / 2 3 / 4 0 / 2 0 / 2 yII C II C x xII C y yII C z II C Y QYP Z NZP M M M Y a Pa M M Z a Pa M T Y a Pa = == = == = = −× = = = ×= = =− × =− ∑ ∑ ∑ ∑ ∑ 9.2. 人字架承受载荷如图所示。试求 I-I 截面上的最大正应力及 A 点的正应力

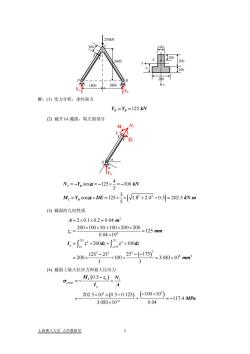
10010020If1o020解：（1）受力分析，求约束力Y, =Y, =125 kN(2）截开1-I截面，取左面部分100kNN,=-Y,sinα:10M, =Y, cosα×DE =125x(V1.8 +2.42 -0.3)= 202.5 kN.m(3）截面的几何性质A=2×0.1×0.2=0.04 m2200×10050+100×00×200125mmz.=0.04×10%I,=2×200dz+x10d1253253253 - (-175)*=3.083×10°mm-200100(4）截面上最大拉应力和最大压应力M,(0.3-z.)MCemay1_202.5×103×(0.30.125) (100×10)-117.4 MPa3.083×10-0.04上海理工大学力学教研室

2400 1800 1800 250kN 300 I I D B C 100 200 200 100 100 z zc y A YD YB 解：(1) 受力分析，求约束力 125 Y Y kN D B = = (2) 截开 I-I 截面，取左面部分 I I D α YD NI QI E MI α ( ) 2 2 4 sin 125 100 5 3 cos 125 1.8 2.4 0.3 202.5 . 5 I D I D N Y kN M Y DE kN m α α =− =− × =− = × = ×× + − = (3) 截面的几何性质 ( ) 2 6 125 25 2 2 25 175 3 3 3 3 8 4 2 0.1 0.2 0.04 200 100 50 100 200 200 125 0.04 10 200 100 125 25 25 175 200 100 3.083 10 3 3 c y A m z m I z dz z dz mm − =× × = × ×+ × × = = × =×+ × − − − = × +× = × ∫ ∫ m ( ) (4) 截面上最大拉应力和最大压应力 ( ) ( ) 1 max 3 3 4 0.3 202.5 10 0.3 0.125 100 10 117.4 3.083 10 0.04 I c c y M z N I A MPa σ − − = − + ×× − − × = − + = − × 上海理工大学 力学教研室 1

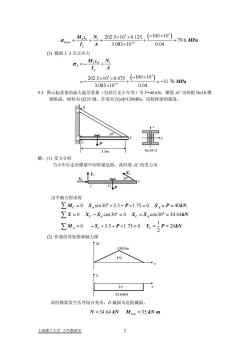
Mz+_202.5×10×0.125(-100×10)79.6MPaatmax3.083×1040.04A(5）截面上A点正应力M,zAMGa =_202.5×10×0.075(100×10)= -51.76 MPa3.083×100.049.3.图示起重架的最大起吊重量（包括行走小车等）为P=40kN，横梁AC由两根No18槽钢组成，材料为O235钢，许用应力[ol=120MPa。试校核梁的强度。ABTpNo18x23.5m解：（1)受力分析当小车行走至横梁中间时最危险，此时梁4C的受力为tYeKSAXcDP由平衡方程求得ZMe=0 S,sin30°×3.5-Px1.75=0 S,=P=40kNZX=0 Xc-S,cos30°=0 X=S,cos30°=34.64kNM,=0-Y×3.5+Px1.75=0Y==P=20kN(2）作梁的弯矩图和轴力图34.64kN此时横梁发生压弯组合变形，D截面为危险截面，N=34.64kN Mmx=35kN.m上海理工大学力学教研室

( ) 3 3 1 max 4 202.5 10 0.125 100 10 79.6 3.083 10 0.04 I c t y M z N MPa I A σ − × × − × = += + = × (5) 截面上 A 点正应力 ( ) 1 3 3 4 202.5 10 0.075 100 10 51.76 3.083 10 0.04 I A A y Mz N I A MPa σ − =− + × × − × = − + = − × 9.3. 图示起重架的最大起吊重量（包括行走小车等）为 P=40 kN，横梁 AC 由两根 No18 槽 钢组成，材料为 Q235 钢，许用应力[σ]=120MPa。试校核梁的强度。 解：(1) 受力分析 当小车行走至横梁中间时最危险，此时梁 AC 的受力为 由平衡方程求得 0 sin 30 3.5 1.75 0 40 0 cos30 0 cos30 34.64 1 0 3.5 1.75 0 20 2 o C A A o o C A C A A C C M S P SP kN X XS XS kN M Y P Y P kN = × −× = = = =− == = = − × +× = = = ∑ ∑ ∑ (2) 作梁的弯矩图和轴力图 30o A C P D Y SA C XC 35kNm (+) x M (-) 34.64kN x N P 30o 3.5m A B C z y No18×2 此时横梁发生压弯组合变形，D 截面为危险截面， max N kN M kN = = 34.64 35 .m 上海理工大学 力学教研室 2

(3）由型钢表查得No.18工字钢A=29.299cm2W,=152cm2(4）强度校核34.64×10335x10NM.Omax =|oemax|--A2W,2x29.299x102x152x106=5.9 +115.1=121 MPa1.05[0]故梁AC满足强度要求。注：对塑性材料，最大应力超出许用应力在5%以内是允许的。9.5.单臂液压机架及其立柱的横截面尺寸如图所示。P=1600kN，材料的许用应力[gF-160MPa。试校核立柱的强度16d3800900400截面I-I2760解：（1）计算截面几何性4 = AaBcp =1.4×0.86=1.204 m2A, = Aabed =(1.4 - 0.05 - 0.016)x(0.86 - 2×0.016)=1.105 m2A=A -A = 0.099 m2截面形心坐标AJie+Ay2eeA1.4-0.05-0.0161.204×0.7+1.105x0.05=0.51 m0.099截面对形心轴的惯性矩Ie=12×0.86×1.43 +(0.7-0.51)°×1.204 = 0.24 m×(0.862×0.016)×(1.40.050.016)I=1+00050=2I. = I, -I1' =0.24-0.211=0.029 m(2）内力分析截开立柱横截面1-I，取上半部分上海理工大学力学教研室

(3) 由型钢表查得 No.18 工字钢 3 2 y = AcmW = 299.29 152 cm (4) 强度校核 3 3 max max max 4 6 34.64 10 35 10 2 2 2 29.299 10 2 152 10 5.9 115.1 121 1.05[ ] c y N M A W MPa σ σ σ − − × × = =+ = + × × ×× =+ = ≺ 故梁 AC 满足强度要求。 注：对塑性材料，最大应力超出许用应力在 5%以内是允许的。 9.5. 单臂液压机架及其立柱的横截面尺寸如图所示。P=1600 kN，材料的许用应力[σ]=160 MPa。试校核立柱的强度。 P 900 1400 2760 3800 I I 1400 yc 890 50 16 16 16 截面 I-I A B C D P a b c d 860 解：(1) 计算截面几何性 ( ) ( ) 2 1 2 2 2 1 2 1.4 0.86 1.204 1.4 0.05 0.016 0.86 2 0.016 1.105 0.099 ABCD abcd A A m A A m AA A m = =× = = = − − × −× = =−= 截面形心坐标 11 2 2 1.4 0.05 0.016 1.204 0.7 1.105 0.05 2 0.51 0.099 c c c Ay Ay y A m + = ⎛ ⎞ − − ×+ × + ⎜ ⎟ ⎝ ⎠ = = 截面对形心轴的惯性矩 ( ) ( ) ( ) 2 3 4 3 2 4 4 1 0.86 1.4 0.7 0.51 1.204 0.24 12 1 0.86 2 0.016 1.4 0.05 0.016 12 1.4 0.05 0.016 0.05 0.51 1.105 0.211 2 0.24 0.211 0.029 I zc II zc I II zc zc zc I m I m III m =× × + − × = = × −× × − − ⎛ ⎞ − − + + ⎜ ⎟ − × = ⎝ ⎠ =−= − = (2) 内力分析 截开立柱横截面 I-I，取上半部分 上海理工大学 力学教研室 3

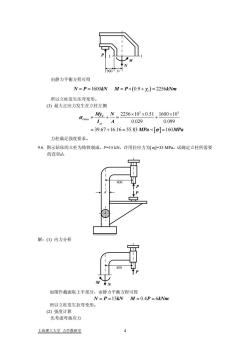
由静力平衡方程可得N=P=1600kNM=Px(0.9+y.)=2256kNm所以立柱发生压弯变形。(3）最大正应力发生在立柱左侧Myc_2256×10×0.51+1600×103Ctmax0.0290.099IA= 39.67 +16.16 = 55.83 MPa[]=160MPa力柱满足强度要求，9.6.图示钻床的立柱为铸铁制成，P=15kN，许用拉应力为[g=35MPa。试确定立柱所需要的直径d。解：(1）内力分析如图作截面取上半部分，由静力平衡方程可得N=P=15kNM=0.4P=6kNm所以立柱发生拉弯变形。(2)强度计算先考虑弯曲应力上海理工大学力学教研室

I I N P 900 M yc 由静力平衡方程可得 N P kN M P y kNm == =× + = 1600 0.9 2256 ( c ) 所以立柱发生压弯变形。 (3) 最大正应力发生在立柱左侧 [ ] 3 3 max 2256 10 0.51 1600 10 0.029 0.099 39.67 16.16 55.83 160 C t zc My N I A MPa MPa σ σ ×× × = += + =+= = ≺ 力柱满足强度要求。 9.6. 图示钻床的立柱为铸铁制成，P=15 kN，许用拉应力为[σt]=35 MPa。试确定立柱所需要 的直径d。 P 400 d P 解：(1) 内力分析 N M P 400 如图作截面取上半部分，由静力平衡方程可得 N P kN M P kNm == = = 15 0.4 6 所以立柱发生拉弯变形。 (2) 强度计算 先考虑弯曲应力 上海理工大学 力学教研室 4

M _32M ≤[0.]W元dd>32M32x6×10=-120.4 mm元[]一元×35×106取立柱的直径d=122mm，校核其强度0m++2M_4x15x10,2×6×10元×0.1222+元×0.1223元d2Td=1.28 +33.66= 34.94MPa[,]立柱满足强度要求。注：在组合变形的截面几何尺寸设计问题中，先根据主要变形设计，然后适当放宽尺寸进行强度校核，这是经常使用的方法。9.7.在力P和H联合作用下的短柱如图所示。试求固定端截面上角点A、B、C、D的正应力。H=5kN解：（1）将力P和H向截面形心简化M=25x103×0.025=625N.m(2)截面ABCD上的内力N= -P=-25 kNM,=M=625N.mM, =H×0.6=3 kN.m(3）截面几何性质A=0.15x0.1=0.015m0.1×0.152 = 3.75×10- mW×0.15×0.1P=2.5×10m(4)A点的正应力NMM_(-25x10)6253000a.=AW.W0.0152.5×103.75×10-1.67×10 + 2.5×10°+ 8×10° =8.83 MPa上海理工大学力学教研室5

[ ] [ ] max 3 3 3 3 6 32 32 32 6 10 120.4 35 10 t t t M M W d M d m σ σ π πσ π == ≤ × × ≥= = × × m 取立柱的直径 d = 122 mm，校核其强度 3 3 max 23 2 4 32 4 15 10 32 6 10 0.122 0.122 1.28 33.66 34.94 [ ] t t NM N M AW d d MPa σ πππ π σ × × ×× =+ = + = + × × =+ = ≺ 3 m 立柱满足强度要求。 注：在组合变形的截面几何尺寸设计问题中，先根据主要变形设计，然后适当放宽尺寸进行 强度校核，这是经常使用的方法。 9.7. 在力 P 和 H 联合作用下的短柱如图所示。试求固定端截面上角点 A、B、C、D 的正应 力。 100 150 600 25 75 50 P=25kN H=5kN z y A B C D P M H z y A B C D My Mz N Q 解：(1) 将力 P 和 H 向截面形心简化 3 M N =× × = 25 10 0.025 625 . (2) 截面 ABCD 上的内力 25 625 . 0.6 3 . y z N P kN M M Nm M H kN m = − =− = = =× = (3) 截面几何性质 2 2 4 2 4 0.15 0.1 0.015 1 0.1 0.15 3.75 10 6 1 0.15 0.1 2.5 10 6 z y A m W m W m − − = ×= =× × = × =× × = × 3 3 (4) A 点的正应力 ( ) 3 4 4 6 66 25 10 625 3000 0.015 2.5 10 3.75 10 1.67 10 2.5 10 8 10 8.83 y z A y z N M M AW W MPa σ − − − × =+ + = + + × × =− × + × + × = 上海理工大学 力学教研室 5

B点的正应力12.+)0=3.83M."A-W,*W.C点的正应力-(-167-25-8) 10=-12.17 MPaAW,W.D点的正应力=(1.67+2.58)×10°=-7.17MPaaD=AWW9.8.作用于悬臂木梁上的载荷为：3y平面内的P=800N，x-平面内的P2=1650N。若木材的许用应力[o-=10MPa，矩形截面边长之比为h/b=2，试确定截面的尺寸。1B解：(1)求内力固定端弯矩最大Mcmx=Px2=1600NmMmm=Px1=1650Nm(2) 求应力木梁在平面弯曲而引起的固定端截面上的最大应力为M3MmaxW.hb?/6木梁在x-平面弯曲而引起的固定端截面上的最大应力为_1.5M,Mgmax"bh/6W.(3)强度计算固定端截面上α点是最大拉应力点，b点是最大压应力点，应力数值大小是3Mam 15Mmm [0]0mx =0ma, +0m =[0]hh33Mmx+1.5Mmm×1600+15×1650=90mmb=10×10%h=2b=180mm上海理工大学力学教研室

B 点的正应力 ( ) 6 1.67 2.5 8 10 3.83 y z B y z N M M MPa AW W σ = − + =− − + × = C 点的正应力 ( ) 6 1.67 2.5 8 10 12.17 y z C y z N M M MPa AW W σ = − − = − − − × =− D 点的正应力 ( ) 6 1.67 2.5 8 10 7.17 y z D y z N M M MPa AW W σ = + − = − + − × =− 9.8. 作用于悬臂木梁上的载荷为：xy平面内的P1=800 N，xz平面内的P2=1650 N。若木材的 许用应力[σ]=10 MPa，矩形截面边长之比为h/b=2，试确定截面的尺寸。 1m 1m x y z O P1 P2 h b a b 解：(1) 求内力 固定端弯矩最大 max 1 max 2 2 1600 1 1650 M P Nm M P N z y = ×= = ×= m (2) 求应力 木梁在 xy 平面弯曲而引起的固定端截面上的最大应力为 max max max max 2 3 3 / 6 zz z z MM M W hb b σ ′ == = 木梁在 xz 平面弯曲而引起的固定端截面上的最大应力为 max max max max 2 3 1.5 / 6 yy y y MM M W bh b σ ′′ === (3) 强度计算 固定端截面上 a 点是最大拉应力点，b 点是最大压应力点，应力数值大小是 [ ] [ ] max max max max max 3 3 3 1.5 Mz My σσσ σ b b =+= + = ′ ′′ σ [ ] max max 3 3 6 3 1.5 3 1600 1.5 1650 90 10 10 2 180 M M z y b m σ h b mm + × +× = = × = = = m 上海理工大学 力学教研室 6

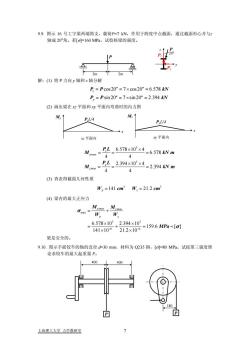
9.9.图示16号工字梁两端简支，载荷P=7kN，作用于跨度中点截面，通过截面形心并与轴成20°角。若[o]=160MPa，试校核梁的强度。[P解：（1）将P力向y轴和=轴分解P, = Pcos20°=7×cos20°= 6.578 kNP, = Psin20° =7×sin20° =2.394 kN(2）画出梁在x=平面和xy平面内弯曲时的内力图M,tM ↑P,L/4炒平面内二平面内PL_ 6.578x10°×4=6.578 kN.mMymaPL_2394x10×4=2.394 kN mMemax4(3）查表得截面几何性质W,=21.2cmW, =141 cm(4)梁内的最大正应力Mymox +MamasGmax:W.6.578×103 2.394x103=159.6 MPa<[α] 141×10-6+21.2×10-6梁是安全的9.10.图示手摇铰车的轴的直径d-30mm，材料为Q235钢，[o]-80MPa。试按第三强度理论求铰车的最大起重量P。100KP回上海理工大学力学教研室

9.9. 图示 16 号工字梁两端简支，载荷P=7 kN，作用于跨度中点截面，通过截面形心并与z 轴成 20o 角。若[σ]=160 MPa，试校核梁的强度。 2m 2m P y z P 20o Py Pz 解：(1) 将 P 力向 y 轴和 z 轴分解 cos 20 7 cos 20 6.578 sin 20 7 sin 20 2.394 o o z o o y P P kN P P k = =× = = =× = N (2) 画出梁在 xz 平面和 xy 平面内弯曲时的内力图 x My PzL/4 x Mz PyL/4 xz 平面内 xy 平面内 3 max 3 max 6.578 10 4 6.578 . 4 4 2.394 10 4 2.394 . 4 4 z y y z P L M k P L M k × × == = × × == = N m N m m (3) 查表得截面几何性质 3 3 141 21.2 W cm W c y z = = (4) 梁内的最大正应力 max max max 3 3 6 6 6.578 10 2.394 10 159.6 [ ] 141 10 21.2 10 y z y z M M W W MPa σ σ − − = + × × =+= × × ≺ 梁是安全的。 9.10. 图示手摇铰车的轴的直径 d=30 mm，材料为 Q235 钢，[σ]=80 MPa。试按第三强度理 论求铰车的最大起重量 P。 P 400 400 P 180 上海理工大学 力学教研室 7

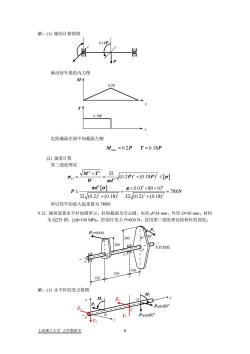
解：（1）轴的计算简图画出铰车梁的内力图MA危险截面在梁中间截面左侧Mmax=0.2PT=0.18P(2)强度计算第三强度理论VM?+T?32. (0.2P) +(0.18P) ≤[0]Trd'[o]元×0.03×80×10%P<=788N32/(0.2) +(0.18)32/(0.2) +(0.18)所以铰车的最大起重量为788N9.12.操纵装置水平杆如图所示。杆的截面为空心圆，内径d=24mm，外径D=30mm。材料为 Q235 钢，[o]=100MPa。控制片受力P=600 N。试用第三强度理论校核杆的强度。解：（1）水平杆的受Su

解：(1) 轴的计算简图 画出铰车梁的内力图 0.18P T 0.2P M x x P 0.18P 危险截面在梁中间截面左侧 max M PT = 0.2 0.18 = P (2) 强度计算 第三强度理论 [ ] [ ] 2 2 2 2 3 3 3 3 6 22 22 32 (0.2 ) (0.18 ) 0.03 80 10 788 32 (0.2) (0.18) 32 (0.2) (0.18) r M T P P W d d P N σ σ π π σ π + = = +≤ × ×× ≤== + + 所以铰车的最大起重量为 788N 9.12. 操纵装置水平杆如图所示。杆的截面为空心圆，内径 d=24 mm，外径 D=30 mm。材料 为 Q235 钢，[σ]=100 MPa。控制片受力 P=600 N。试用第三强度理论校核杆的强度。 100 250 150 200 300 P1=600N P2 80o A B C D 至控制舵 解：(1) 水平杆的受力简图 P1 M1 M2 P2sin80o P2cos80o A B C D x y z ZA YA YC ZC 上海理工大学 力学教研室 8

M, = P ×0.2 = 600×0.2 =120 N.mM, = P, sin80°x0.3=0.295P,列平衡方程ZM,=0 M,=M, 120=0.295P, P=406.8N.mZM,=0Y×0.4-P,cos80x0.5=0Yc=88.3NZY=0Yc-Y,-P, cos80°=0 Y,=17.66 NZM,=0P×0.15+Zc×0.4-P, sin80°×0.5=0 Zc=275.8 NZz=0- Zc+ P, sin80° = 0Z, = 475.2 NZ.-P画出内力图M.tM,t.28N.m2.649N.m7.064N.m炒平面内x平面内T +B截面是危险截面Mg=M,+M=71.28°+2.649=71.32N.m(2）按第三强度理论计算32/M,+T?3271.32°+1202= 89.2 MPa<[α]0=D(-)元x003(-24/30)杆的强度足够9.14.图示带轮传动轴传递功率P=7kW，转速n=200r/min。皮轮重量0=1.8kN。左端齿轮上的啮合力P.与齿轮节圆切线的夹角（压力角）为20%。轴的材料为Q255钢，许用应力[o]=80 MPa。试分别在忽略和考虑带轮重量的两种情况下，按第三强度理论估算轴的直径。解：(1)传动轴的计算简图上海理工大学力学教研室

1 1 2 2 2 0.2 600 0.2 120 . sin80 0.3 0.295 o M P N m M P P =× = × = = ×= 列平衡方程 1 2 2 2 2 2 1 2 1 2 0 120 0.295 =406.8 . 0 0.4 cos80 0.5 0 88.3 0 cos80 0 17.66 0 0.15 0.4 sin80 0.5 0 275.8 0 sin x o z C C o C A A o y C C A C M M M P P Nm MY P Y N Y YY P Y N MP Z P Z Z Z PZ P == = = ×− ×= = = −− = = = × +×− ×= = = −− + ∑ ∑ ∑ ∑ ∑ 80 0 475.2 o = = Z N A N 画出内力图 x My 71.28N.m x Mz xz 平面内 xy 平面内 40.06N.m 7.064N.m 2.649N.m x T 120N.m B 截面是危险截面 22 2 2 71.28 2.649 71.32 . M MM B By Bz = += + = N m (2) 按第三强度理论计算 ( ) ( ) 2 2 2 2 3 3 44 3 4 4 32 32 71.32 120 89.2 [ ] 1 / 0.03 1 24 / 30 B r M T MPa D dD σ σ π π + + == = − ×− ≺ 杆的强度足够. 9.14. 图示带轮传动轴传递功率P=7 kW，转速n=200 r/min。皮轮重量Q=1.8 kN。左端齿轮上 的啮合力Pn与齿轮节圆切线的夹角（压力角）为 20o 。轴的材料为Q255 钢，许用应力 [σ]=80 MPa。试分别在忽略和考虑带轮重量的两种情况下，按第三强度理论估算轴的 直径。 A B φ300 φ500 200 400 200 T1=2T2 T2 Pn 20o Q 解：(1) 传动轴的计算简图 上海理工大学 力学教研室 9