内蒙古科技大学：《材料力学》课程教学资源（习题辅导）弯曲应力

第六章弯曲应力第六章弯曲应力6.1钢丝直径d=0.4mm，弹性模量E=200GPa若将钢丝弯成直径D=400mm的圆弧时，试求钢丝横截面上的最大弯曲正应力。（200MPa）解：钢丝的弯矩和中性层曲率半径之间的关系为：1_M"EIMym，由弯曲正应力公式得m=EJ则：M=，钢丝弯成圆弧后，产生的弯0D+dD曲变形，其中性层的曲率半径p=E(S)_Ed_200×10*×04=200MPaCmx =-D"D40026.2矩形截面梁如图所示。b=8cm，h=12cm试求危险截面上a、d三点的弯曲正应力。(20.8MPa, 10.4MPa, 0)解：由平衡方程ZM,(F)=0得到：F,=Fs=1×2×4=4KN+FR危险截面在梁的中点处Mm=q*-+×2×4=4KNm4KVxbxh?-×80x1203=1152×10*mmF1:12e4KNMya=0g. =4KNmMMy.4×10°×30田机械=10.42MPaa1152×104I.M44x10°×60=20.83MPaqa=土术1152×104④M4KNm

第六章 弯曲应力 第六章 弯曲应力 6.1 钢丝直径 d=0.4mm, 弹性模量 E=200GPa, 若将钢丝弯成直径 D=400mm 的圆弧时，试求 钢丝横截面上的最大弯曲正应力。（200MPa） 解：钢丝的弯矩和中性层曲率半径之间的关系为： EI M =  1 则：  EI M = ，由弯曲正应力公式得   max max My = =  Eymax ，钢丝弯成圆弧后，产生的弯 曲变形，其中性层的曲率半径 2 2 D d D  +  = 2 ) 2 ( max D d E  = = = D Ed 200MPa 400 200 10 0.4 3 =   6.2 矩形截面梁如图所示。b = 8cm, h =12cm, 试求危险截面上 a、c、d 三点的弯曲正应力。 （20.8MPa, 10.4MPa, 0） 解：由平衡方程 M A (F) = 0  得到： FA FB 2 4 4KN 2 1 = =   = 危险截面在梁的中点处： M ql 2 4 4KNm 8 1 8 1 2 2 max = =   = I z = 12 1 2  b  h = 3 4 4 80 120 1152 10 12 1   =  mm MPa I My MPa I My I My z d d z c c z a a 20.83 1152 10 4 10 60 10.42 1152 10 4 10 30 0 4 6 4 6 =    = = =    = = = =    FA FB 4KN Fs  4KN 4KNm M 4KNm  M 机械 土木

第六章弯曲应力6.3从直径为d的圆木中截取一矩形截面梁，试根据强度观点求出所截取的矩形截面的最合理的高h和宽b。(h=a,b=a)yMa ya=-M.解：最大弯曲正应力：OmaxW7h/b的最佳值应应使梁的抗弯截面系数为最大。抗弯截面系数：W=bh -b(d?-b")=(d'b-b)为b为自变量的函数。W_d-36-0电dtadh=Va--b _ V6db=36.4图示两根简支梁，其跨度、荷载及截面面积都相同。一个是整体截面梁，另一个是由两根方木叠置而成（二方木之间不加任何联系），试画出沿截面高度的弯曲正应力分布图，并分别计算梁中的最大弯曲正应力。mT1（翡啡）aa解：做出梁的弯矩图如右所示：（1）对于整体截面梁：-9机械W.=bh =-la.(2a)-2a土木-qM3ql故：0mx916aWaVK（2）对于两根方木叠置A由于这是两个相同的方木叠合而成，VA且其之间不加任何的联系，故有7M,=M,--M.W.--a,M.2Gg)_3Omex8aW-00

第六章 弯曲应力 6.3 从直径为 d 的圆木中截取一矩形截面梁，试根据强度观点求出所截取的矩形截面的最合 理的高 h 和宽 b。(h= d 3 6 , b= d 3 3 ) 解：最大弯曲正应力： z Wz M y I M max max max  max = = h/b 的最佳值应应使梁的抗弯截面系数为最大。抗弯截面系 数： ( ) 6 1 ( ) 6 1 6 1 2 2 2 2 3 W = bh = b d − b = d b − b 为 b 为自变量的函数。 由 0 6 3 2 2 = − = d b dt dW 3 6 3 3 3 2 2 2 d d h d b d b = = = − = 6.4 图示两根简支梁，其跨度、荷载及截面面积都相同。一个是整体截面梁，另一个是由两 根方木叠置而成（二方木之间不加任何联 系），试画出沿截面高度的弯曲正应力分布 图，并分别计算梁中的最大弯曲正应力。 （ 3 2 16a 3ql , 3 2 8a 3ql ） 解：做出梁的弯矩图如右所示： （1）对于整体截面梁： 2 2 3 3 2 (2 ) 3 1 6 1 Wz = bh = a  a = a 故： 3 2 3 2 max max 16 3 3 2 8 1 a ql a ql W M z  = = = （2）对于两根方木叠置 由于这是两个相同的方木叠合而成， 且其之间不加任何的联系，故有 3 2 3 2 1 1 max 3 1 2 max 8 3 6 1 ) 8 1 ( 2 1 , 6 1 , 2 1 a ql a ql W M M M M W a z z =  = = = = =  3 2 16 3 a ql 3 2 16 3 a ql M 2 8 1 ql  机械 土木 M 2 8 1 ql  3 2 8 3 a ql 3 2 8 3 a ql 3 2 8 3 a ql

第六章弯曲应力6.5某梁的矩形截面如图，弯曲剪力Q,=40kN，求截面上a、b、c三点的弯曲剪应力。(t,=2MPa,T,=1.5MPa,T-0解：从图形上可以看出截面形心在其对称中心上，150F.且有1，=bh"=×150×200*=10mm→81量图S.=50×150×75=5.625×10°mmyt再有矩形截面梁的弯曲正应力F,s:3xFs_340×103，故。=0,T==2.0 MPa1.b2*A2*150×20040×1056251015 MTh=10°×1501.b6.6图示简支梁由三块木板胶合而成，I=-1m，胶缝的许用剪应力为[]=0.5MPa，木材的许用弯曲正应力为[o]-10MPa，许用剪应力为[1]=1MPa,试求许可荷载 P。(P=8.1kN）f解：依题给条件，对梁进行受力分析，由平衡条件，列平衡方程，做出剪力图H1.90和弯矩图如右所示（1）按木材弯曲正应力强度要求确定许可荷载I Pl=Px1P-2≤[0]=10max×90×1202④=P≤8640N0（2）按木材剪应力强度要求确定许可荷载PHP3F_3[]=Tmex:2*90×120= P≤14400N（3）按胶合面剪应力强度要求确定许可荷载④Ipx(40×90×40)土木t-Fss!≤[]= 0.51.b×90×1203×90P≤8100N综上所述可知 P=8100N=8.1KN

第六章 弯曲应力 6.5 某梁的矩形截面如图，弯曲剪力 Qy＝40kN，求截面上 a、b、c 三点的弯曲剪应力。 （ 2MPa a = ， 1.5MPa b = ，  c = 0 ） 解：从图形上可以看出截面形心在其对称中心上， 且有 3 3 8 4 150 200 10 12 1 12 1 I z = bh =   = mm 5 3 Sz = 5015075 = 5.62510 mm 再有矩形截面梁的弯曲正应力 I b F S z S z   = ，故 = 0, c  2.0 150 200 40 10 2 3 2 3 3 =   =  =  A FS a  MPa 1.5 10 150 40 10 5.625 10 8 3 5 =     = =  I b F S z S z b  MPa 6.6 图示简支梁由三块木板胶合而成，l=1m, 胶缝的许用剪应力为 = 0.5MPa ，木材的许用 弯曲正应力为 =10MPa ，许用剪应力为  =1MPa ， 试求许可荷载 P。（P=8.1kN） 解：依题给条件，对梁进行受力分析， 由平衡条件，列平衡方程，做出剪力图 和弯矩图如右所示 （1）按木材弯曲正应力强度要求确定许可荷载   10 90 120 6 1 1 4 1 4 1 2 max max  =     = = =  P W Pl W M  P  8640N （2）按木材剪应力强度要求确定许可荷载   1 90 120 2 1 2 3 2 3 max  =   =  =   P A FS  P 14400N （3）按胶合面剪应力强度要求确定许可荷载   0.5 90 120 90 12 1 (40 90 40) 2 1 ' 3 '  =       = =    P I b F S z S z  P  8100N 综上所述可知 P=8100N=8.1KN Fs 2 P Pl 4 1 M 2 P Pl 4 1 机械 土木

第六章 弯曲应力6.7在图a中，若以虚线所示的纵向面和横向面从梁中截出一部分，如图b所示，试求在纵向面abcd上由tdA组成的内力系的合力，并说明#它与什么力平衡。（-器（1-x)x）解：有剪应力互等定律可知，纵向截面上剪应力与横向截面上剪应力大小相等，(b)中性层上剪应力变化规律为：3(ql - gx)3g(1 - 2x)7(t)= 3F,(2)2 Bh4.Bh24A纵截面 abcd上剪应力合力为：t(s)F =I'-(0)8-dt=-T'340-2)B.d4BhPo(s)3gx(1 - 2x)4h6.8图示梁由两根36a工字钢铆接而成。铆钉的间距为s=150mm，直径d=20mm，许用剪应力[]=90MPa。梁横截面上的剪力F,=40kN。试校核铆钉的剪切强度。（t=16.2MPa）解：查表可得，36.α工字钢的惯性矩PP66鼎1.=15800cml，截面面积A=76.48cm截面高度h=36cm。组合惯性矩为I=2(1. +d’A)=2(15800+18 ×76.48)= 81200cmt一根工字钢的截面对中性轴的静面矩为：S=18×76.48=1380cmFSc40×1031380×10-6铆钉连接处的纵截面上的剪力流：=68KN/m81200×10-8120折有铆钉间距S=得每个铆钉承受的剪力为：Qm=号_0.15x68x10=5100N2Q铆铆钉的剪应力：=16.2 MPa []-90 Mpa×3.14×d2故，校核安全

第六章 弯曲应力 6.7 在图 a 中，若以虚线所示的纵向面和横向面从梁中截出一部分，如图 b 所示，试求在纵 向面 abcd 上由 dA 组成的内力系的合力，并说明 它与什么力平衡。（Q= (l x)x 4h 3q − ） 解：有剪应力互等定律可知，纵向截面 上剪应力与横向截面上剪应力大小相等， 中性层上剪应力变化规律为： ( ) ( ) ( ) Bh q l x Bh ql qx A F x x S 4 3 2 2 2 1 3 2 3 − =       −  = = 纵截面 abcd 上剪应力合力为： ( ) ( ) ( ) h qx l x B dx Bh q l x F x B dx x x 4 3 2 4 3 2 0 0 − =  − =  =    6.8 图示梁由两根 36a 工字钢铆接而成。铆钉的间距为 s=150mm, 直径 d = 20mm, 许用剪应 力 = 90MPa 。梁横截面上的剪力 Fs = 40kN。试校核铆钉的剪切强度。（ ＝16.2MPa ） 解：查表可得，36 a 工字钢的惯性矩 4 Ι z =15800cm ，截面面积 2  = 76.48cm 截面高度 h = 36cm。组合惯性矩为 ( ) ( ) 2 2 4 Ι z c = 2 Ι z + d A = 2 15800 +18  76.48 = 81200cm 一根工字钢的截面对中性轴的静面矩为： 3 Szc =18 76.48 =1380cm  铆钉连接处的纵截面上的剪力流： KN m I F S f z zc 68 / 81200 10 40 10 1380 10 8 3 6 =     = = − −  有铆钉间距 f Q S 2 铆 = ，得每个铆钉承受的剪力为： N sf Q 5100 2 0.15 68 10 2 3 =   铆 = = 铆钉的剪应力： 16.2 3.14 4 1 2 =   = d Q铆  MPa    =90 Mpa 故，校核安全。 a ' a ' b ' c c b d 2 h ' a a b ' b (x)  (x)

第六章弯曲应力6.9半径为r的圆形截面梁，切掉画阴影线的部分后，反而有可能使抗弯截面模量增大（何故？）。试求使W为极值的α，并问这对梁的抗弯刚度有何影响？（α=78°）解：切掉阴影部分后剩余的面积，是由4个相同的直角三角形和4个相同的扇形面积组成，一个直角三角形面积对水平直径的惯性矩为Ii=bh ={(rsin a)(rcosa)Ir.cosa.sina个扇型面积对水平直径的惯性矩为：I2α = Jy d4- I (osn o) (o-do.dp)-Ip'dpl'sin*0do-(-sina12因为圆截面在中性轴附近聚集了较多的材料而离中性轴远处的材料却较少，当切掉适当的小弓形面积后，使之离中性轴远处的材料密集度增大，因而抗弯截面系数笔增大。剩余面积对水平直径的惯性矩为：-(4α - sin 4a)I, = 4/1, +4/2 =r4sin2a+rcosa-sin2(4a-sin 4a)_r(4a-sin 4a)抗弯截面系数：W.4sin a8sin aw-_[(4-4cos* dkin a-(4a-sin*a)osa|-0da8sin’a= (4 - 4 cos4a)sin a-(4a-sin 4a)cos a = 0=α=0或者a=78°Wmx =0.791r3,1,=0.774r4W,=↓x3.14xr =0.785r3未切前I, =↓x3.14xrt =0.785r4比较后可知，切后抗弯截面系数增大，而抗弯刚度降低，因而使梁的抗断能力提高，抗弯曲变形能力降低

第六章 弯曲应力 6.9 半径为 r 的圆形截面梁，切掉画阴影线的部分后，反而有可能使抗弯截面模量增大（何 故？）。试求使 W 为极值的  ，并问这对梁的抗弯刚度有何影响？（ O  = 78 ） 解：切掉阴影部分后剩余的面积，是由 4 个相同的直角三角形和 4 个相同的扇形面积组成， 一个直角三角形面积对水平直径的惯性矩为： ( ) ( ) r a a I bh r a r a x 3 3 3 3 1 cos sin 4 1 sin cos 4 1 4 1 =  = = 一个扇型面积对水平直径的惯性矩为： ( ) ( )       =  = − =   =       a r a d d d d I y dA r a r A x sin 4 1 4 2 sin sin 4 0 0 3 2 0 2 2 2          因为圆截面在中性轴附近聚集了较多的材料而离中性轴远处的材料却较少，当切掉适当的小 弓形面积后，使之离中性轴远处的材料密集度增大，因而抗弯截面系数笔增大。剩余面积对 水平直径的惯性矩为： ( a a) r a r a a a I I I r x x x 4 sin 4 8 sin 2 cos sin 4 1 2 4 4 4 4 4 3 1 2  +  = −      = + = − 抗弯截面系数： ( ) ( ) a r a a a a a y I W x x 8sin 4 sin 4 4sin 4 sin 4 8 1 3 max − = − = = ( ) ( ) ( ) ( )  0 78 4 4cos 4 sin 4 sin 4 cos 0 0 sin 4 4cos sin 4 sin cos 8 2 3 4 4  = =  − − − =  =      − − − = a a a a a a a a r a a a a a da dWx 或者 3 W max 0.791r x = ， 4 I 0.774r x = 未切前 4 4 3 3 3.14 0.785 4 1 3.14 0.785 4 1 I r r W r r x x =   = =   = 比较后可知，切后抗弯截面系数增大，而抗弯刚度降低，因而使梁的抗断能力提高，抗弯曲 变形能力降低

第六章弯曲应力6.10试求图示梁的最大弯曲正应力和最大弯曲剪应力。（提示：tm发生在中性轴上。）（omx=9.00MPa，Tmx =1.05MPa )NFAFal_10×3=15KN解：Fs.m2010×32g1(15KN=11.25KNmMmexFe1,=(200*-100*)=1.25x10°mm15KNS=100×200x50-100×50×25=875000mm11.25KNmM11.25×10%?×100=9.00MPa机械Gmexymm=125×10%FsmxS15x103×8750001.05MPa1.25×10%×100土术1.bM田11.25KNm6.11图示铸铁梁，材料的许用拉应力[o.]=40MPa，许用压应力[oJ=100MPa，1,=5965cm*，yc=157.5mm。试校核梁的强度。（ocmax- 52.8MPax=26.4MPa)F,-20×1+10×2×5=30KNF-20kNg=10kN/mOEY+_20×3_10×2×1=10NFR=广mEFaa42m,M,=20KNm,M,=10KNm10KNy=230-157.5=72.5mm20×10%×72.5 = 24.31MPaGlmxe5965x10410KN20×106Om-My.=20KN= 5965x10×157.5=52.81MPaM,10KNmM10×106M,x157.5=26.40MPa02max5965×104110×106M×72.5 =12.16MPaM,20KNmm5965x104Cecmx = 52.81MPa≤[α ]O1f,mx = 26.40MPa≤[0,]

第六章 弯曲应力 6.10 试求图示梁的最大弯曲正应力和最大弯曲剪应 力。(提示： max  发生在中性轴上。)（ 9.00MPa max = ， 1.05MPa max = ） 解： KN ql Fs 15 2 10 3 2 ,max =  = = KNm ql M 11.25 8 10 3 8 2 2 max =  = = * 2 4 4 8 4 100 200 50 100 50 25 875000 (200 100 ) 1.25 10 12 1 S mm I mm z z =   −   = = − =  y MPa I M z 100 9.00 1.25 10 11.25 10 8 6 max max max  =    = = MPa I b F S z s z 1.05 1.25 10 100 15 10 875000 8 3 * ,max max =      = = 6.11 图示铸铁梁，材料的许用拉应力   40MPa t = ，许用压应力   100MPa c = ， 4 z I = 5965cm ， yC =157.5mm 。试校核梁的强度。（ 52.8MPa c max = ， 26.4MPa t max = ） FA 30KN 4 10 2 5 4 20 1 =   +  = FB 10KN 4 10 2 1 4 20 3 =   −  = M1 = 20KNm,M2 =10KNm y1 = 230 −157.5 = 72.5mm y MPa I M y MPa I M y MPa I M y MPa I M c z c z t c z c z t 72.5 12.16 5965 10 10 10 157.5 26.40 5965 10 10 10 157.5 52.81 5965 10 20 10 72.5 24.31 5965 10 20 10 4 6 1 2,max 4 6 1 1 2,max 4 6 1 1,max 4 6 1 1 1,max  =   = =  =   = =  =   = =  =   = =     26.40 [ ] 52.81 [ ] ,max ,max t t c c MPa MPa     =  =  10KN 10KN 20KN20KNm10KNm   Fs M M1 M2 FA FB 1 y 15KN11.25KNm   Fs M 15KN 11.25KNm M  机械 土木 FA FB

第六章弯曲应力6.12图示一铸铁梁，材料的许用拉应力与许用压应力之比为[o,]/o。]-1/3，试求水平翼缘板的合理宽度b。（b=316mm）60×b×30+340×30×(340+60)yi=60×b+340x3030b+170×230b+170J; = 400→) = 400~30b+170×230_ 370b+170×170b+170b +170兰=[0,] O t,maxMy2=[o,]Gc.mμ_ [o,]y2[o.]30b+170×230370b +170×1703370b +170×170 = 90b +170×690_170×690170×170315.72mmh-370-906.13图所示矩形截面悬臂梁，承受载荷 F,和Fz作用，且F,=Fz=F=1.0kN,截面高度h=80mm，宽度b=40mm，许用应力[o]=160MPa，a=800mm。试校核梁的强度。1yMM..x=F,a=1.0×800=800KNmmMy.mx=F,×2a=1.0×1600=1600KNmmAtyMm Mym(a)OmaxMW.W,1600×103800x103My.m×40×802=×80×402=18.75+ 75 = 93.75MPa [0]

第六章 弯曲应力 6.12 图示一铸铁梁，材料的许用拉应力与许用 压应力之比为 t /c  =1/ 3 ，试求水平翼缘板 的合理宽度 b。（b=316mm） 170 30 170 230 60 340 30 60) 2 340 60 30 340 30 ( 1 + +  =  +    +   + = b b b b y 170 370 170 170 170 30 170 230 2 400 1 400 + +  = + +  = − = − b b b b y y [ ] [ ] ,max 2 ,max 1 c z c t z t y I M y I M     = = = = [ ] [ ] 2 1 c t y y   = b mm b b b b 315.72 370 90 170 690 170 170 370 170 170 90 170 690 3 1 370 170 170 30 170 230 = −  −  = +  = +  = +  +  6.13 图所示矩形截面悬臂梁，承受载荷 Fy 和 Fz 作用，且Fy = Fz = F = 1.0 kN,截面高度h = 80 mm，宽度b = 40 mm，许用应力  =160MPa ，a = 800 mm。试校核梁的强度。 M z,max = Fya = 1.0800 = 800KNmm M y,max = Fy  2a = 1.01600 = 1600KNmm 18.75 75 93.75 [ ] 80 40 6 1 1600 10 40 80 6 1 800 10 2 3 2 3 ,max ,max max   = + =     +    = = + MPa W M W M y y z z 2 y 1 y M z,max M y,max

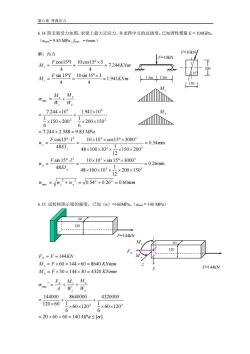
第六章弯曲应力6.14简支梁受力如图，求梁上最大正应力，并求跨中点的总挠度。已知弹性模量E=100GPa(omax=9.83MPa,Jmax=6mm）F=10kN/解：内力[F=10kN>MsosFsm15%_10sin15×3=1.941KmM.:1.5m/1.5m150MM+M,CmExW."w,7.244×10°1.941×10%Mx150×2002×200×1502= 7.244 + 2.588 = 9.83 MPaFcos15°.j310×10×cos15×30003= 0.54mmw.=48EI48×100×10×150×200312Fsin15°.1310×103×sin15°×30003w.:0.26mm48El,48×100×10×200×1503Wmx=/w +w,=0.54*+0.262=0.60mm6.15试校核图示梁的强度。已知（o）=160MPa。（omx=140MPa）120F-144klFv = F =144KNM.=F×60=144×60=8640KNmmF=144kNM,=F×30=144×30=4320KNmmE+M..MTWW14000+86400004320000120×60×60×1202=×60×1202= 20 +60 + 60=140 MPa[α]

第六章 弯曲应力 6.14 简支梁受力如图，求梁上最大正应力，并求跨中点的总挠度。已知弹性模量 E = 100GPa。 （σmax= 9.83 MPa , fmax = 6mm） 解：内力 KNm F l M KNm F l M z z 1.941 4 10sin 15 3 4 sin 15 7.244 4 10cos15 3 4 cos15 =  =  = =  =  = MPa W M W M y y z z 7.244 2.588 9.83 200 150 6 1 1.941 10 150 200 6 1 7.244 10 2 6 2 6 max = + =    +    =  = + w w w mm EI F l w EI F l w z y y y z z 0.54 0.26 0.60 0.26mm 200 150 12 1 48 100 10 10 10 sin 15 3000 48 sin 15 0.54mm 150 200 12 1 48 100 10 10 10 cos15 3000 48 cos15 2 2 2 2 max 3 3 3 3 3 3 3 3 3 3 = + = + = =         =  = =         =  = 6.15 试校核图示梁的强度。已知〔σ〕=160MPa。（σmax = 140 MPa） M F KNmm M F KNmm F F KN y z N 30 144 30 4320 60 144 60 8640 144 =  =  = =  =  = = = 20 60 60 140 [ ] 60 120 6 1 4320000 60 120 6 1 8640000 120 60 144000 2 2 max   = + + =    +   +  = = + + MPa W M W M A F y y z N z t F=144kN 120 60 120 60 F=144kN z y M y M z FN 150 200 15° F=10kN 1.5m 1.5m F=10kN M z M y

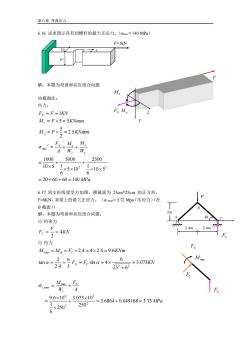
第六章弯曲应力6.16试求图示具有切槽杆的最大正应力。（omax=140MPa）F=1kN解：本题为弯曲和拉压组合问题M由截面法：内力：FNMyFN=F=IKNM,=Fx5=5KNmm=2.5KNmmM,=FxCmey_ 10005000250010x51×5×102=×10×526= 20 + 60 + 60 = 140 MPa6.17简支折线梁受力如图，横截面为25cm*25cm的正方形，F=8KN，求梁上的最大正应力。（ocmax=3.72Mpa（压应力）（在B截面））解：本题为弯曲和拉压组合问题：1）约束力2.4mFe=号=4KN1)内力MMx=Mg=Fc×2.4=4×2.4=9.6KNm9F=Fesinα=4xtan α= 24==3.073KNV5? +62Mmx+ENO.e.mexW9.6×10°3.073×10= 3.6864 + 0.049168 = 3.73 MPa2502×25036

第六章 弯曲应力 6.16 试求图示具有切槽杆的最大正应力。（σmax = 140 MPa） 解：本题为弯曲和拉压组合问题 由截面法： 内力： M F KNmm M F KNmm F F KN y z N 2.5 2 5 5 5 1 =  = =  = = = MPa W M W M A F y y z N z t 20 60 60 140 10 5 6 1 2500 5 10 6 1 5000 10 5 1000 2 2 max = + + =   +   +  =  = + + 6.17 简支折线梁受力如图，横截面为 25cm*25cm 的正方形， F=8KN，求梁上的最大正应力。（σc max= 3.72 Mpa（压应力）（在 B 截面）） 解：本题为弯曲和拉压组合问题： 1) 约束力 KN F FC 4 2 = = 1) 内力 MMax = MB = FC  2.4 = 4 2.4 = 9.6KNm 5 6 2.4 2 tan = = FN FC 3.073KN 5 6 6 sin 4 2 2 = + =  =  MPa A F W M N z c 3.6864 0.049168 3.73 250 3.073 10 250 6 1 9.6 10 2 3 3 6 max ,max = + =  +   =  = + F=1kN 5 10 10 A 2.4m 2.4m 2m C B F FC  FC FN Mmax FS z y M y M z F FN