内蒙古科技大学：《材料力学》课程教学资源（习题解答）能量方法和静不定结构

13.1.两根圆截面杆材料相同，尺寸如图所示，一根为等截面杆，一根为变截面杆，试比较两杆的变形能。TT[2]31/8IPLP(a)解：方法1:两杆的变形PL4PLP(3L/8),P(L/4) 7PLNlo"EA"ErN(b) =2x*En(2d)/4End’/4"4Ed?外力的功2P°L7P?LWoa- plo-SEaWo--Plo,- Erl功能原理2PL7P2LUea=Wo-ErtUe,=Won=sErt方法2：两杆的内力N(a) =P N(b)=P变形能_N?L_PL_ 2P2LUa=2EA-2E元d/4E元dp2(3L/8)P (L/4)_7P°LU(b) =22E元(2d)/42End/48End13.2.图示杆架各杆的材料相同截面面积相等，在P力作用下，试求桁架的变形能YT解：(I)求约束力

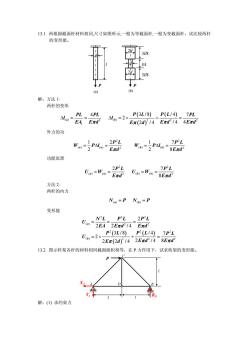
13.1. 两根圆截面杆材料相同,尺寸如图所示,一根为等截面杆,一根为变截面杆，试比较两杆 的变形能。 l 3l/8 d 3l/8 d 2d 2d l/4 P P (a) (b) 解：方法 1: 两杆的变形 ( ) ( ) ( ) ( ) 2 2 ( ) 2 1 4 7 3 /8 /4 2 2 /4 /4 4 a b PL PL P L PL PL l l 2 EA Ed π E d π Ed Ed π π Δ = = Δ =× + = 外力的功 2 2 ( ) ( ) 2 2 ( ) ( ) 12 1 7 2 2 a a b b P L P L W Pl W Pl Eπd E8 πd = Δ= = Δ= 功能原理 2 2 () () 2 2 () () 2 7 8 a a b b P L P L UW UW Eπd Eπd == == 方法 2: 两杆的内力 ( ) ( ) N PN P a b = = 变形能 ( ) ( ) ( ) 22 2 ( ) 2 2 2 2 2 ( ) 2 2 2 2 2 2 /4 3 /8 /4 7 2 2 2 /4 2 /4 8 a b NL PL PL U EA E d E d P L PL P L U E d E d E π π π π πd == = = × + = 13.2. 图示杵架各杆的材料相同截面面积相等，在 P 力作用下，试求桁架的变形能。 RB A D B l l YA XA P C l 解：(1) 求约束力

ZX=0 P-X,=0 X,=PZM^=0 R×21-Pxl=0 Rs=PZY=0 Re-Y=0 Y,=P(2)分析铰BRCNBD +V21Nc=N2R,=NRD=R(3)分析铰DANDNDANNDA=NDe=ND-NDc=0(4)分析铰 CAAV2PNe=Nc =NBc (5）桁架的变形能UZ-ilNlNN)）)(（（1+)-0.957号=2EAEA2213.3.计算图示各杆的变形能MY21/3(c)解： (b)上海理工大学力学教研室

0 0 0 2 0 2 0 0 2 A A A B B BA A X PX X P P M R l Pl R P Y RY Y = −= = = × − ×= = = −= = ∑ ∑ ∑ (2) 分析铰 B NBC B NBC NBD RB 45o NBD RB 2 2 2 2 BD B BC B P P NR N R == = = (3) 分析铰 D D NDC NDA NDB 0 2 DA DB BD DC P NNN N = == = (4) 分析铰 C NCA P C NCA NCB NCB P 2 2 CA CB BC P NNN === (5) 桁架的变形能 ( ) ( ) 2 22 22 2 2 2 2 1 2 2 1 2 1 2 2 2 2 0.957 2 2 22 2 i i BC BC AC AC BD BD DA DA N l U N l N l N l N l EA EA P P Pl l l P l EA EA = = +++ ⎡ ⎤ ⎛ ⎞ ⎛⎞ ⎛ ⎞ = × × +× × = + = ⎢ ⎥ ⎜ ⎟ ⎜⎟ ⎜ ⎟ ⎝⎠ ⎝ ⎠ ⎝ ⎠ ⎣ ⎦ ∑ EA 13.3. 计算图示各杆的变形能。 θ ds dθ EI R (c) P B A O A M (b) B EI C l/3 2l/3 解：(b) 上海理工大学 力学教研室 1

方法1：(1）查表得C截面的转角MTe= EN--9E(2)由功能原理M"lU=W=Me =-18EI方法2(1)列出梁的弯矩方程M8LELMI[M(x)=- x,Mx,+MM(x2)=-(2) 求弯曲变形能M’18M1Ml- a+ 2EI162EI162EI18EI(e)(1）列出梁的弯矩方程N(O)M(0)=-PRsino(2) 求弯曲变形能-I s-Irn ro2EI-元P"R8EI13.4.传动轴受力情况如图所示，轴直径为40mm，E=210GPa，G=80GPa。试计算轴的变形能。2上海理工大学力学教研室

方法 1： (1) 查表得 C 截面的转角 2 2 2 4 3 3 6 99 C M ll l 9 Ml EIl EI θ ⎛ ⎞ = − × − × =− ⎜ ⎟ ⎝ ⎠ (2) 由功能原理 2 1 2 18 C M l UW M EI == = θ 方法 2 (1) 列出梁的弯矩方程 x1 A M B EI C M/l M/l x2 1 1 2 2 ( ) ( ) M Mx x l M Mx x M l ⎧ = − ⎪⎪ ⎨ ⎪ = − + ⎪⎩ (2) 求弯曲变形能 2 22 2 /3 1 2 1 2 0 /3 () () 8 2 2 162 162 18 l l l M x M x Ml Ml Ml U dx dx 2 EI EI EI EI = + =+ ∫ ∫ EI = (c) (1) 列出梁的弯矩方程 M θ )( = −PRsinθ (2) 求弯曲变形能 2 2 / 2 0 2 3 ( ) ( sin ) 2 2 8 l M PR U ds EI EI P R Rd EI θ θ π θ π − == × = ∫ ∫ 13.4. 传动轴受力情况如图所示，轴直径为 40 mm，E=210 GPa，G=80 GPa。试计算轴的变 形能。 θ R P B O Q(θ) M(θ) N(θ) 上海理工大学 力学教研室 2

解：(1)传动轴受力Z.=Z=0.5 kNY, = Yg =0.18 kN(2）弯矩方程和扭矩方程M,(x)=Zgx=500xM,(x)=Y,x=180xT(x)=80(3) 变形能U =2].2J。2GI,2EI(0)+(8))2GIp[500 +180 2)210×10×元×0.04*/643(80) ×0.2+2×80×10×元×0.04*/32=0.0604 J(4)使用功能原理求解本题U=W=↓PS,+PJ+↓ToP3PP1TxTx1/2-T1=1×P,×48E1*2×P×48EI,2a1 e(++ )+,0.4380°×0.41 021010 04 (-0 100)4 0 010 0 -32=0.0604 J13.7.试用互等定理求跨度中点C的挠度，设EI=常量。[P上海理工大学力学教研室

A B 200 C 200 0.08kN.m 0.36kN 1kN 解：(1) 传动轴受力 0.5 0.18 Z Z kN Y Y kN A B = = == A B (2) 弯矩方程和扭矩方程 M x Zx x M x Yx x T x y A zA ( ) = = == = 500 ( ) 180 80 ( ) (3) 变形能 ( ) ( ) ( ) ( ) () () ( ) ( ) 2 2 0.2 0.2 0.2 0 00 2 0.2 0.2 2 2 0 0 3 3 2 2 9 4 2 9 4 500 180 80 2 2 2 22 1 80 0.2 500 180 2 1 0.2 500 180 210 10 0.04 / 64 3 3 80 0.2 2 80 10 0.04 / 32 0.0604 y z P x x U dx dx EI EI GI x dx x dx EI GI J π π =++ × = ++ ⎛ ⎞ = × ⎜ ⎟ × ×× ⎝ ⎠ × + × × ×× = ∫ ∫∫ ∫ ∫ 2 0.2 P dx + × (4) 使用功能原理求解本题 ( ) ( ) 3 3 3 2 2 2 3 2 2 2 9 4 9 4 1 11 2 22 1 1 1/ 2 2 48 2 48 2 96 4 0.4 80 0.4 360 1000 96 210 10 0.04 / 64 4 80 10 0.04 / 32 0.0604 yy zz y z y z y z z yP U W Pf Pf T P l P l Tl l T l P P T PP E P I EI GI EI J φ π π == + + × =× × +× × + × = + + × = + + × × ×× × × ×× = GI 13.7. 试用互等定理求跨度中点 C 的挠度，设 EI=常量。 A B (a) C D a l/2 l/2 P l/2 l/2 P B A C (b) A B YA C 0.36kN 1kN 0.08kN. 0.08kN.m m ZA ZB YB 上海理工大学 力学教研室 3

解：(a)(1）将P力移到C截面处，如下图(2）由位移互等定理PI?Pal?e =81 =8/2 =0g ×a:16E*"16EI方向向上(b) (1)将P力移到C截面处，如下图[P(2）由位移互等定理_P(/2)+[_P(1/2)5PIJe=8 =82= fe+0 ×13EI2EI248EI1方向向下13.8.车床主轴可简化成EI=常量的当量轴，如图所示，试求在载荷P作用下，截面C的挠度和前轴承B处的截面转角。IPYRB解：(1)约束反力Ra=lp Re-2(2) 弯矩方程M(x)=-Px M(x)=-=Px,(3）在C处作用单位集中力 截面C的挠度上海理工大学力学教研室

解：(a) (1) 将 P 力移到 C 截面处，如下图 2 A B C D P 1 (2) 由位移互等定理 2 2 21 12 16 16 C B Pl Pal f aa EI E = = = ×= ×= δδθ I 方向向上 (b) (1) 将 P 力移到 C 截面处，如下图 P B A C 2 1 (2) 由位移互等定理 ( ) ( ) 3 2 3 21 12 /2 /2 5 2 3 2 2 48 C C C l l Pl Pl f f Pl EI EI δδ θ ⎡ ⎤ = = = + × =− + − × =− ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ EI 方向向下 13.8. 车床主轴可简化成 EI=常量的当量轴，如图所示，试求在载荷 P 作用下，截面 C 的挠 度和前轴承 B 处的截面转角。 A B C a P 4a x2 x1 RA RB 解：(1) 约束反力 1 5 4 4 R PR A B = = P (2) 弯矩方程 () ( ) 11 2 1 4 M x Px M x Px = − = − 2 (3) 在 C 处作用单位集中力 11 1 ( ) 2 ( 2 2 ) 1 4 Mx x Mx x = − = − 截面 C 的挠度 A B C 1 x2 x1 1/4 5/4 上海理工大学 力学教研室 4

[ M(x)M(a)ax +JM(xs)M(x)axfe=J.EIA(x(-+ px ) (-4r (-Px) (-x) d + 5PaLdx, =(0)3EIEET(4)在B处作用单位集中力偶1/4alM(s)=0 M(s)--*:截面B的转角0.-I ()()a +,(()4:E()(-)4Pa4a=0+dx, =EI3EI顺时针转向13.9.试求图示各梁截面B的挠度和转角。EI-常量al解：（1）在B处作用虚加力P和M，并列出弯矩方程raM(x)=-P,x- - M,M(x)=-{qx; -P,(I-a+x)-M,(2）上式分别对P和M求偏导数M(x) =-xiOM(x.) =-(1-a+x.)aP,aP0M(x.) = -1aM(x) =-1aM,aM,(3）用卡氏定理求挠度和转角上海理工大学力学教研室

( ) ( ) ( ) ( ) ( )( ) ( ) 1 2 1 11 2 12 1 2 22 3 4 1 1 1 2 0 0 1 1 4 4 5 3 C l l a a Mx M x Mx M x f dx dx EI EI Px x Px x Pa dx dx EI EI EI = + ⎛ ⎞⎛ ⎞ ⎜ ⎟⎜ ⎟ − ×− − ×− ⎝ ⎠⎝ ⎠ =+ = ∫ ∫ ∫ ∫ ↓ (4) 在 B 处作用单位集中力偶 A B C x2 x1 1 1/4a 1/4a 2 1 ( ) 2 2 ( ) 2 1 0 4 Mx Mx x a = = − 截面 B 的转角 ( ) ( ) ( ) ( ) 1 2 1 21 2 22 1 2 22 2 4 2 0 1 1 4 4 4 0 3 B l l a Mx M x Mx M x dx dx EI EI Px x a Pa dx EI EI θ = + ⎛ ⎞⎛ ⎞ ⎜ ⎟⎜ ⎟ − ×− ⎝ ⎠⎝ ⎠ = + = ∫ ∫ ∫ 顺时针转向 13.9. 试求图示各梁截面 B 的挠度和转角。EI=常量 a l q B C A (a) 解：(1) 在B处作用虚加力Pf和Mf，并列出弯矩方程 x1 Mf q B C A x2 Pf 2 1 1 2 2 2 ( ) 1 () ( ) 2 f f f f Mx Px M M x qx P l a x M =− − =− − − + − (2) 上式分别对Pf和Mf求偏导数 1 2 1 2 1 2 () () ( ) () () 1 1 f f f f Mx Mx x l P P Mx Mx M M ∂ ∂ = − =− − + ∂ ∂ ∂ ∂ = − = − ∂ ∂ a x (3) 用卡氏定理求挠度和转角 上海理工大学 力学教研室 5

ou-[ M(x) aM(x)dx +J M(x,) M(x) dx,fBaP,JEIOP,EIaP,-Im2(-n)a EI2x--P(I-a+x)-M,+[-(1 - a + x2)]dx,EI- U-[ (M(d++JMETM,[ M(x,) M() te,.-0M,-I. ET oM,Igx -P,(l-a+x,)-M,- P2(-14+ --(-1)dx,EEI（4）令上两式中的P和M为零qxq_(4 -a)fs=0+()[-(1-a +x,)]dx, =-EI24EI1aqa0,=0+J°E1(-1)de=EI挠度和转角的方向与虚加力的方向一致13.11.图示刚架各杆的的EI相等。试求A的位移和截面C的转角。a+国(a)解：(a)应用莫尔定理（1）刚架各段的弯矩方程M(x)=PxM(x)=0 M(x)=Pb(2)在A处垂直方向作用单位集中力t!国M(x)=0 M(x2)=x2M(x)=aA的垂直位移上海理工大学力学教研室

1 2 2 1 2 1 1 2 2 1 2 1 1 1 0 2 2 2 2 0 1 1 2 2 1 2 1 1 0 () () () () ( ) ( ) 1 ( ) 2 [ ( )] () () () () ( ) ( 1) B l l ff f l a f f a f f B l l ff f l a f f U Mx Mx Mx Mx f dx dx P EI P EI P Px M x dx EI qx P l a x M l a x dx EI U Mx Mx Mx Mx dx dx M EI M EI M Px M dx EI θ − − ∂∂ ∂ = = + ∂∂ ∂ − − = − − − −+ − + − − + ∂∂ ∂ = = + ∂∂ ∂ − − = − ∫ ∫ ∫ ∫ ∫ ∫ ∫ 2 2 2 2 0 1 ( ) 2 ( 1) a f f qx P l a x M dx EI − − −+ − + − ∫ （4）令上两式中的Pf和Mf为零 2 2 2 3 2 2 0 2 3 2 0 1 2 0 [( )] (4 24 1 2 0 (1) 6 a B a B qx qa f l a x dx l a) EI EI qx qa dx EI EI θ − =+ −−+ = − − =+ − = ∫ ∫ 挠度和转角的方向与虚加力的方向一致 13.11. 图示刚架各杆的的 EI 相等。试求 A 的位移和截面 C 的转角。 A C a b h x2 x1 x3 P (a) 解：(a) 应用莫尔定理 (1) 刚架各段的弯矩方程 M x Px M x M x Pb ( ) 11 2 3 = = 0 ( ) ( ) = (2) 在 A 处垂直方向作用单位集中力 1 Mx Mx x Mx a 1 1 ( ) == = 0 12 2 13 ( ) ( ) A C x2 x1 x3 A 的垂直位移 上海理工大学 力学教研室 6

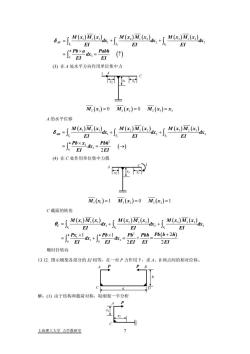
+[ M(s)M(a)dx,[()()a+()() +8Av=J,EIEIEI-I Pxa-Foh (1)0FIFI(3)在A处水平方向作用单位集中力国M,(μ)=0 M,(r)=0 M,(r)=x)A 的水平位移8m((+(+(M(x,)M,(x)axEIEIEIPbh?Pbx dx,= 2EI()JoEI(4）在C处作用单位集中力偶FxxM,(m)=1 M,()=0 M,(x)=1C截面的转角[()()+()()+),[ M(x)M(x)axec=J.EIEIEIPb2Pbh_Pb(b+2h)PxXldx,2EI+ET2EI顺时针转向13.12.图示刚架各部分的EI相等一对P力作用下，求A、B两点间的相对位移。PP解：（）由于结构和载荷对称，取刚架一半分析+上海理工大学力学教研室

( ) ( ) ( ) ( ) ( ) ( ) ( ) 12 3 1 11 2 12 3 13 1 2 3 0 AV ll l h Mx M x Mx M x Mx M x dx dx dx EI EI EI Pb a Pabh dx 3 EI EI δ =+ + × = =↑ ∫∫ ∫ ∫ (3) 在 A 处水平方向作用单位集中力 A C x2 x1 x3 1 Mx Mx Mx x 2 1 ( ) = = 0 0 2 2 ( ) 2 3 ( ) = 3 A 的水平位移 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 12 3 1 21 2 22 3 23 1 2 2 3 3 0 2 AH ll l h Mx M x Mx M x Mx M x dx dx dx EI EI EI Pb x Pbh dx 3 EI EI δ =+ + × = =→ ∫∫ ∫ ∫ (4) 在 C 处作用单位集中力偶 A C x2 x1 x3 1 Mx Mx Mx 3 1 ( ) =1 0 1 3 2 ( ) = = 3 3 ( ) C 截面的转角 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 12 3 1 31 2 32 3 33 1 2 2 1 1 3 0 0 1 1 2 + = 2 2 C ll l b h Mx M x Mx M x Mx M x dx dx dx EI EI EI Px Pb Pb Pbh Pb b h dx dx 3 EI EI EI EI EI θ =+ + × × + = += ∫∫ ∫ ∫ ∫ 顺时针转向 13.12. 图示刚架各部分的 EI 相等，在一对 P 力作用下，求 A、B 两点间的相对位移。 C A B D P P h a 解：(1) 由于结构和载荷对称，取刚架一半分析 C A P x1 x2 上海理工大学 力学教研室 7

(2)弯矩方程M()=PxM(x)=PhaM(μ)=xaM (x.) =hapap(3）应用卡氏定理apaPPhPah_Ph (2h+3a)EI3EI2EI6EI(4)4、B间的相对位移Ph (2h+ 3a)8AB=283EIA、B两点相互靠近。13.13.图示桁架各杆的材料相，截面面积相等，在载荷P作用下，试求节点B与D间的相对位移。解：（1）在B处作用虚加力Ps，并求出约束反力4IaXx=P+, Y=P N,=P+p,(2) 求各杆的轴力--号，-N4=2P+P, N,=0(3)上式分别对P求偏导数上海理工大学力学教研室

(2) 弯矩方程 ( ) ( ) ( ) ( ) 11 2 1 2 1 M x Px M x Ph Mx Mx x h P P = = ∂ ∂ = = ∂ ∂ (3) 应用卡氏定理 ( ) ( ) ( ) ( ) ( ) 1 2 1 1 2 2 1 2 3 2 2 / 2 1 1 1 2 0 0 2 3 32 6 A l l h a Mx Mx Mx Mx dx dx EI P EI P Px x Ph h Ph Pah Phha dx dx EI EI EI EI EI δ ∂ ∂ = + ∂ ∂ × × + = + =+ = ∫ ∫ ∫ ∫ (4) A、B 间的相对位移 ( ) 2 2 3 2 3 AB A Phha EI δ δ + = = A、B 两点相互靠近。 13.13. 图示桁架各杆的材料相，截面面积相等，在载荷 P 作用下，试求节点 B 与 D 间的相 对位移。 A B l P l C D 解：(1) 在B处作用虚加力Pf，并求出约束反力 ND Pf A B 5 4 3 2 XA D C P 1 YA 2 2 2 2 XA =+ = =+ P P Y PN P fA D Pf (2) 求各杆的轴力 123 4 5 2 2 2 2 2 0 2 2 f f f f N PN PN P N PP N = − = − =− − =+ = P (3) 上式分别对Pf求偏导数 上海理工大学 力学教研室 8

aN-_V2aN2-=1ON5=0ap2ap2ap2aP,ap,(4）用卡氏定理求B点沿BD方向的位移--NONaP,EAoP,E(号)喜叫鸟)-EAEA(-P-p).1(P+P)21.1+0EAEA(5）令上式中的P为零8m-0+++0-(+)-271EAEAFA方向为B向D靠近13.14.图示简易吊车的撑杆AC长为2m，截面的惯性矩I=8.53×10°mm。拉杆BD的A=600mm2。P-2.83kN。如撑杆只考虑弯曲影响，试求C点的垂直位移，设E=200GPa。家解：（1)求出约束反力PR,=V2Pp =(2)求BD杆的轴力和AC杆的弯矩-px M(x,)=--p(+x,)+V2PxN=2p M(x)=-上海理工大学力学教研室

1 2 3 5 4 222 1 0 222 f f f ff N N N N N P P P PP ∂ ∂ ∂ ∂ ∂ = − =− =− = = ∂ ∂ ∂ ∂∂ (4) 用卡氏定理求 B 点沿 BD 方向的位移 5 1 2 2 2 2 2 2 () () 2 2 2 ( ) 2 (2 ) 2 2 ( ) 1 2 ii i BD f f i f f f f U Nl N P EA P P l P l EA EA P Pl PP l 0 EA EA δ = ∂ ∂ = = ∂ ∂ −⋅ −⋅ = −+ − −− ⋅ + ⋅ + − + ⋅ ∑ + (5) 令上式中的Pf为零 ( ) 2 (2) 2 2 0 0 ( ) 0 ( 2) 2.71 2 2 BD P l Pl Pl Pl EA EA EA δ − ⋅ ⋅ =++ − + += + ≈ EA 方向为 B 向 D 靠近 13.14. 图示简易吊车的撑杆AC长为 2 m，截面的惯性矩I=8.53×106 mm 4 。拉杆BD的A=600 mm 2 。P=2.83 kN。如撑杆只考虑弯曲影响，试求C点的垂直位移，设E=200 GPa。 P A B D C 45o 45o 1m 解：(1) 求出约束反力 2 2 2 2 2 XAAD === PY PR P (2) 求 BD 杆的轴力和 AC 杆的弯矩 1 12 2 2 2 2 ( ) ( ) (1 ) 2 2 2 N P M x Px M x P x Px = = − = − ++ 2 RD x1 P A B D C 45o 45o x2 XA YA 上海理工大学 力学教研室 9