内蒙古科技大学：《材料力学》课程教学资源（习题辅导）弯曲变形

第七章弯曲变形第七章弯曲变形7-1用积分法求位移时，下列各等直梁应分几段？写出各梁中AB段的挠曲线近似微分方程。写出确定积分常数的位移边界条件和变形连续条件。解：应该分为3段取 CD为研究对象得：B1C ElDIFe = Fp=ql取整体为研究对象得：Fa=gt,Fa=qlEhg-(0I)FEnt=-n-x) (ssnEhg=q(21-x,)--q(21-x,)(1x, 21)W, ls=-0= w, ls=-= 0W2 la-/ = 0Wa l.-g=w l,-M=FZFwil.g wil.EI隆Ws lsg=2/= 0解：应该分为2段FcF=0,Fc=F(b)Ehw'= Fl(0≤x,≤1)Ew' = F(21 -x2)(1≤x≤21)w, ls- = 0W, ls-/-= W2 lsg=/w/ x-/= w2 lsg=-FW2 /xz =2/= -k

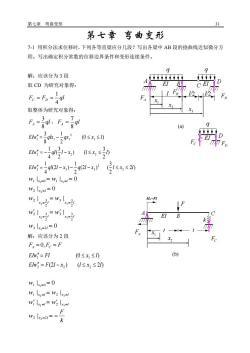
第七章 弯曲变形 31 第七章 弯曲变形 7-1 用积分法求位移时，下列各等直梁应分几段？写出各梁中 AB 段的挠曲线近似微分方 程。写出确定积分常数的位移边界条件和变形连续条件。 解：应该分为 3 段 取 CD 为研究对象得： F F ql C D 4 1 = = 取整体为研究对象得： F ql A 8 3 = ， F ql A 8 7 = 2 ) 2 3 (2 ) ( 2 1 (2 ) 4 1 ) 2 3 ) (l 2 3 ( 4 1 (0 ) 2 1 8 3 3 2 3 3 3 2 2 2 1 2 1 1 1 EIw ql l x q l x l x l EIw ql l x x l EIw qlx qx x l  = − − −    = − −    = −   | 0 | | | | | 0 | | 0 3 2 2 3 3 2 2 3 2 3 3 2 2 3 2 1 0 1 3 2 3 2 3 2 1 1 =  =  = = = = = = = = = = = = x l x l x l x l x l x l x x l w w w w w w w w 解：应该分为 2 段 FA = 0,FC = F (2 ) ( 2 ) (0 ) 2 2 2 1 1 EIw F l x l x l EIw Fl x l  = −    =   k F w w w w w w x l x l x l x l x l x = −  =  = = = = = = = = 2 2 1 2 1 2 1 0 2 2 3 2 3 1 | | | | | | 0 1 x (a) 2 x 3 x FA FD FB FD FC (b) FA 1 x 2 x FC

第七章弯曲变形327.2用积分法求图示梁跨度中点的挠度w_和端截面转a5ql47q13角A及（Wc768E10,=384EITm3glV2+ V2+0g =.128ET解：Fa-gl:Fa=glEh=q2g(x-)Ehi=gt, (0≤xs)(G≤x,≤1)Eh - oah: -goEni- gki c.-g(-+C,Ehn= g4t + 3+D,Eha=gk'--29(-*++D,边界条件：wi ls=-0=0= D, =04891-W2 ls-/= 0=1-24.169*+C /+ , =0W --=W2 .--=C()+D, =C()+ D,l--w---C=C,=0则: D,=D,=0, C=C,=-3849lEm-94-（En-oai- aEn-1-_7q13g/30,=w l.-0=-0g=W/ lk 28EI384EI5gl1r1qic--3849(G) =-Wc = Wi = E4890384EI

32 第七章 弯曲变形 7.2 用积分法求图示梁跨度中点的挠度 wc 和端截面转 角  A 及  B 。（ EI ql wC 768 5 4 = ， EI ql A 384 7 3  = ， EI ql B 128 3 3  = − ） 解： F ql A 8 1 = ； F ql B 8 3 = 1 1 1 3 1 1 1 2 1 1 1 1 1 48 1 16 1 ) 2 (0 8 1 EIw qlx C x D EIw qlx C l EIw qlx x = + +  = +  =   2 2 2 4 2 3 2 2 2 3 2 2 2 2 2 2 2 2 2 ) 2 ( 24 1 48 1 ) 2 ( 6 1 16 1 ) 2 ) ( 2 ( 2 1 8 1 C x D l EIw qlx q x C l EIw qlx q x x l l l EIw qlx q x = − − + +  = − − +  = − −   边界条件： 1 | 0 0 1 w x = =  0 D1 = | 0 2 2 w x =l =  0 24 16 1 48 1 2 2 4 4 + + =  ql − ql C l D 2 2 2 1 2 3 | | l x l x w w = = =  1 1 2 2 ) 2 ) ( 2 ( D l D C l C + = + 2 2 2 1 2 3 | | l x l x w w = =  =   0 C1 = C2 = 则： 0 D1 = D2 = ， 4 1 2 384 7 C = C = − ql 2 3 1 1 1 1 3 3 1 1 384 7 16 1 ) 2 (0 384 7 48 1 EIw qlx ql l EIw qlx ql x x  = − = −   384 7 ) 2 ( 6 1 16 1 ) 2 ( 384 7 ) 2 ( 24 1 48 1 3 3 2 2 2 2 2 2 4 3 2 3 2 2 ql l EIw qlx q x x l l ql x l EIw qlx q x  = − − − = − − −   EI ql A w x 384 7 | 3 1 0 1  =  = = − EI ql B w x l 128 3 | 3 2 2  =  = = EI l ql ql l ql EI wC w 384 5 )] 2 ( 384 7 ) 2 ( 48 1 [ 1 3 3 3 = 1 = − = − 2 x FA FB 1 x

第七章弯曲变形7.3用叠加法求下列各梁的指定位移。gl5ql40=913Aa(wc48EI4EI&1mmITm1V2(a) , 8c(alx)x1qlx(b)qt3qt3Wcql =3EI3EI×2"24EI*12E.ql3Iqt?Wc24EI*248EIqt35q13qt8E7-48E7 - 48L ()We=Wcal +Wcq(qx)x1qlx(5)7q13Ocqi=O2EI3EI24EIqtOcaEI24EI7q13ql?912Oc =Ocql +0cg=24EI24EI4EI(C),31g13169ql4c.(wc384ET-0g=48EIWay = 9lx(_ =3EI3EI1qx(/)x()qx()qx(l)4qx(b)35g13x+Wc =[-8E]-1+[2x(_)]+[1EI3EI2EI384EIqlt35gl3=163g13We=Wcal +Wcg3EI384EI384EIg1×12qt3Ocql =2EI2EI-1gx()qx(gx)x()(5)=7g13Oca=6EI2EIEI)-48EI7q1331ql3q13Oc = Ocal +Oc. =2E*48EI48EI

第七章 弯曲变形 33 7.3 用叠加法求下列各梁的指定位移。 a.( EI ql wC 48 5 4 = ， EI ql C 4 3  = ) ( ) 48 5 8 48 24 2 48 3 2 24 12 8 ) 2 ( 3 ) 2 ( 3 3 3 3 3 3 3 3 3 = + = − =  = −  = −  = + =   +  = EI ql EI ql EI ql w w w EI l ql EI ql w EI ql EI ql EI l ql EI l l ql EI l ql w C Cql Cq Cq Cql EI ql EI ql EI ql EI ql EI ql EI l l ql EI l ql C Cql Cq Cq Cql 24 24 4 7 24 24 7 3 ) 2 ( 2 ) 2 ( 3 2 2 3 3 2 = + = − = = − =   +  =      c.( EI ql wC 384 169 4 = , EI ql C 48 31 3  = ) EI ql EI ql EI ql EI l ql EI l q EI l l q EI l q EI ql EI ql l EI ql EI ql EI ql w w w EI l ql EI l q l EI l q l EI l l q EI l q w EI ql EI ql l w C Cql Cq Cq Cql C Cql Cq Cq Cql 48 31 48 7 2 48 7 ) 2 ( ) 2 ( 2 1 2 ) 2 ) ( 2 ( 6 ) 2 ( 2 2 384 163 384 35 3 384 35 )] 2 ( 2 ) 2 ( ) 2 ( 3 ) 2 ( )] [ 2 ( ) 2 ) ( 2 ( 2 1 ] [ 8 ) 2 ( [ 3 3 ( ) 3 3 3 3 3 2 2 2 3 4 3 3 3 3 3 4 2 3 4 = + = + =  =  +   +  = =  = = + = + =  =   +   +   +  = =  =     

34第七章弯曲变形d(we = 5ga=24.0%=%）P=qoqa (2a)ga41qatmWcgxam3EI24EI8EI_qax(2a)qaxa=-Wcq =16EI4EI(d)8c11qat_ gat-5qWe=wcal+wca24EI4EI=24EIqa (2a)qa3qaOcq =6E3EI2EI_ qax(2a)2-_ qaOcp=4EI16EIqa_ qa_ qa0c = Oca + Ocpa2EI 4EI4EIm+++mm(e) Vs安+TTT5qae.(WB =16EI5q(2a)*_ 5qaWRI384EI24EI1 × 5g(2a)_ 5qa*Wo2=×384EI=48E5qa+5qa_5qatWB=WB1+WB224EI48EI16EI

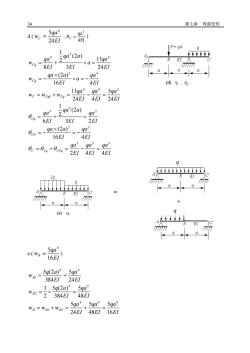
34 第七章 弯曲变形 d.( EI qa wC 24 5 4 = , 4EI qa 3 C = ) EI qa EI qa EI qa EI qa EI qa a EI qa EI qa a EI qa EI qa EI qa EI qa w w w EI qa a EI qa a w EI qa a EI qa a EI qa w C Cq CPq CP Cq C Cql Cq Cq Cq 2 4 4 16 4 (2 ) 3 2 (2 ) 2 1 6 24 5 24 4 11 16 4 (2 ) 24 11 3 (2 ) 2 1 8 3 3 3 2 3 3 2 3 4 4 3 2 4 4 2 4 = + = − = = −  = − = + = = + = − =  = −  = − = +  =      e.( EI qa wB 16 5 4 = ) EI qa EI qa EI qa w w w EI qa EI q a w EI qa EI q a w B B B B B 16 5 48 5 24 5 48 5 384 5 (2 ) 2 1 24 5 384 5 (2 ) 4 4 4 1 2 4 4 2 4 4 1 = + = + = =  = = = = q q +

第七章弯曲变形7.4求图示组合梁的最大弯矩（用力法求解静不定）。C点为梁间铰。（Mmax=4Pa/5）2ELKa(P-F)a)wr3EIF(2a)3Wc2=3(2EI)Wc=Wc2(P-F)aF(2a)3P3EI3(2EI)F-sM.mPaMam=Pa

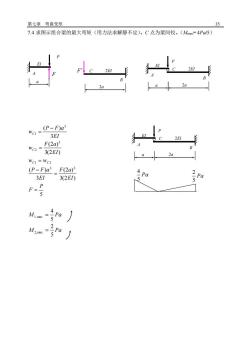
第七章 弯曲变形 35 7.4 求图示组合梁的最大弯矩（用力法求解静不定）。C 点为梁间铰。（Mmax= 4Pa/5） 5 3(2 ) (2 ) 3 ( ) 3(2 ) (2 ) 3 ( ) 3 3 1 2 3 2 3 1 P F EI F a EI P F a w w EI F a w EI P F a w C C C C = = − = = − = M Pa 5 4 1.max = M Pa 5 2 2,max = P A C B EI 2EI a 2a P A EI a F C B 2EI 2a F P A C B EI 2EI a 2a Pa 5 2 Pa 5 4

36第七章弯曲变形7.5作图示刚架的弯矩图，刚架各杆的EI皆相等。(Mmax=Ma=3qcz/8)布qE"F一三F6E1xa=90We, = ga(山)6EIa_Feaxa=4Fca(↑)Wcre3EI3EIEI4Fcaqa3=0Wcy=Wca-1Ver6EI3EIFc=qaMmx=Fc7.6图示刚架，弯曲刚度EI为常数，试画刚架的弯矩图。0M.a?Maxa=3M ()WcM2EIEI2EIFea_Feax4Fca3xa(↑)WCF.3EIEI3EI3M,a24Fca3=0Wo,=Wq+WcFe2EI3EI9M.Fc=-8a

36 第七章 弯曲变形 7.5 作图示刚架的弯矩图，刚架各杆的 EI 皆相等。(Mmax= MA=3qa2 /8) F qa EI F a EI qa w w w EI F a a EI F a EI F a w EI qa a EI qa w C C Cy Cq CF C C C CF Cq C C 8 1 0 3 4 6 ( ) 3 4 3 ( ) 6 6 3 3 3 3 2 3 = = − = − = = −  =  =  =  2 2 2 2 max 8 3 2 1 8 1 2 1 M = FC a − qa = qa − qa = − qa 7.6 图示刚架，弯曲刚度 EI 为常数，试画刚架的弯矩图。 a M F EI F a EI M a w w w EI F a a EI F a EI F a w EI M a a EI M a EI M a w e C e C Cy Cq CF C C C CF e e e CM C C 8 9 0 3 4 2 3 ( ) 3 4 3 ( ) 2 3 2 2 3 3 3 2 2 = − = + = + = = −  =  = +  =  C B A q a a FC C B A q a a FC FC