内蒙古科技大学：《材料力学》课程教学资源（习题辅导）拉伸、压缩与剪切

第二章 拉伸、压缩与剪切第二章拉伸、压缩与剪切2.1求图示各杆指定截面的轴力，并作轴力图。(a)解：4 40kN 3 50kN 225kN 1_20kNHFOTFr=5kNF4. FN.F40kN 3FRENFN=Fr=5 kNFN,=FR+40=45 kN225kN20kNF20kMFNFN=-25+20-5 kNFN,=20kN45kN20kN5kN田田SLN

第二章 拉伸、压缩与剪切 3 第二章 拉伸、压缩与剪切 2.1 求图示各杆指定截面的轴力，并作轴力图。 FR 40kN 50kN 25kN 1 20kN 2 1 2 3 3 4 4 （a） 4 4 FR FN4 40kN 3 FR FN3 25kN 20kN 2 2 FN2 1 20kN 1 FN1 解： FR=5kN FN4=FR=5 kN FN3=FR+40=45 kN FN2=-25+20=-5 kN FN1=20kN 45kN 5kN 20kN 5kN

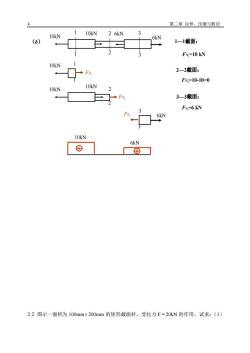
第二章 拉伸、压缩与剪切10kN26kN10kN6kN1-1截面;(b)FN,=10 kN10kN2—2截面;FN=10-10=010kN10kN3—3截面：Fn=6 kNFN6kN10kN6kN田田2.2图示一面积为100mm×200mm的矩形截面杆，受拉力F=20kN的作用，试求：（1）

4 第二章 拉伸、压缩与剪切 （b） 10kN 10kN 6kN 6kN 3 3 2 2 1 1 10kN 6kN FN1=10 kN FN2=10-10=0 FN3=6 kN 1—1截面： 2—2截面： 3—3截面： 10kN FN1 1 1 10kN 10kN 2 2 FN2 6kN 3 3 FN3 2.2 图示一面积为 100mm  200mm 的矩形截面杆，受拉力 F = 20kN 的作用，试求：（1）

第二章 拉伸、压缩与剪切0=的斜截面m-m上的应力：（2）最大正应力αm和最大剪应力tm的大小及其作用面的方位角。解：F_ 20×103=1MPaF:A0.1x0.2m3=0.75MPa030°=0cos~α=1x1x%sin60°==0.433MPaT30°2Omax==1MPa=0.5MPaTmax22.3图示一正方形截面的阶梯形混凝土柱。设重力加速度g=9.8m/s混凝土的密度为p=2.04x10°kg/m2，F=100kN，许用应力[0]=2MPa。试根据强度条件选择截面宽度a和b

第二章 拉伸、压缩与剪切 5 6   = 的斜截面 m-m 上的应力；（2）最大正应力 max 和最大剪应力 max  的大小及其作用 面的方位角。  F F m m 解： 3 20 10 1MPa 0.1 0.2 P A   = = =  2 30 3 cos 1 0.75MPa 4    = =  = 30 1 3 sin60 0.433MPa 2 2 2   = =  = max  = =1MPa max 0.5MPa 2   = = F 2.3 图示一正方形截面的阶梯形混凝土柱。设重力加速度 g = 9.8m/s2 , 混凝土的密度为 3 3  = 2.0410 kg / m ，F = 100kN，许用应力 = 2MPa 。试根据强度条件选择截面宽度 a 和 b

第二章 拉伸、压缩与剪切6IFP = 2.04×103 ×9.8 = 2×104 N/m2解：FFv_F+ p.4a?FN/=F+p.4d?,01==[]Aa2回100×103=0.228m≥--210-4×2×10FN2=3.F+p.4a?+p.4b2=3×100×103+2×104×4×0.2282+2×104×4×b2304.16×103FN2=0.398m=398mm≥[a],h>2V2×106_4×2×104h22.4在图示杆系中，AC和BC两杆的材料相同，且抗拉和抗压许用应力相等，同为[o]。BC杆保持水平，长度为I，AC杆的长度可随e角的大小而变。为使杆系使用的材料最省试求夹角的值

6 第二章 拉伸、压缩与剪切 b F 4m 4m F F a b F 4m 4m F F a 解： 2 1 N P a = +   4 ,3 4 2  =   =  2.04 10 9.8 2 10 N/m 2 1 1 2 1 4 [ ] N P a A a    +  = = = 3 6 4 100 10 0.228m [ ] 4 2 10 4 2 10 P a     = = −  −   2 2 2 3 4 2 4 2 3 4 4 3 100 10 2 10 4 0.228 2 10 4 N P a b b = +  +    =   +    +    2 2 2 [ ] , N b   =  3 6 4 304.16 10 0.398m 398mm 2 10 4 2 10 b   = =  −   FN1 FN1 FN2 FN2 F F F F 2.4 在图示杆系中，AC 和 BC 两杆的材料相同，且抗拉和抗压许用应力相等，同为 。 BC 杆保持水平，长度为 l，AC 杆的长度可随  角的大小而变。为使杆系使用的材料最省， 试求夹角  的值

第二章拉伸、压缩与剪切解KZF,=0,Fn2sn0-F=0,FN2sin ecOsOZF=0Fac0-Fm=0,FFN2FNI1cosoFA2 =A[o][]sino[o][o]sinoA,1Fl1cosO+A1=V=V+V, -cosesincosesinFl(tan 0+2 cot 0)[o]_ sin 0+ cos? 01= tanθ+ cot0)(sin 0cos0sincoso由=0,(tan 0 =-1,(ctg0)=-sindecos?0d12(tan 0+2ctg0) ==0decos"のsin"?sin?0-2cos?0=0,sin?0-2cos?0=0sin?0cos?0tan?0=2, tan0= V2,0= 54.44°

第二章 拉伸、压缩与剪切 7 F FN2 FN1 C F FN2 FN1  C F   sin 0 , sin 0 , 2 2 F FY = FN − F = FN = FX FN FN FN F    sin cos 0 , cos 0 , 2 1 1  = − = =     1 1 1 , sin N A P    = =     2 2 cos sin N A P     = = FN2 FN1 A2 F A1 F 解：   ) sin cos sin cos 1 ( cos 1 2 1 2       = + = + = + Fl Al A l V V V   (tan 2cot)  = + Fl tan cot ) sin cos sin cos sin cos 1 ( 2 2         = + + =      2 2 sin 1 , ( ) cos 1 0 ,(tan ) − =  = ctg  = d d 由 V 0 sin 2 cos 1 (tan 2 ) 2 2 + = − =      ctg d d 0 ,sin 2cos 0 sin cos sin 2cos 2 2 2 2 2 2 = −  =   −   54.44 tan 2 , tan 2 , 2 = = =   

第二章拉伸、压缩与剪切2.5图示桁架ABC，在节点C承受集中载荷F作用。杆1与杆2的弹性模量均为E，横截面面积分别为Ai=2580mm2,A=320mm2。试问在节点B与C的位置保持不变的条件下，为使节点C的铅垂位移最小，θ应取何值（即确定节点A的最佳位置)。AA解：Fv=Fcoto, F2=F/sin0-Fwil_Fcoto.1A, :EAEAF.1Fn2l2Al, =EAEA sin OcosoFNAN.NFI1coteFNACysinetaneE sin Ocos QA,"A,tanedACy=0d(8+cos'0)dedo(sinocoso)0 = 55.7°2.6图示杆的横截面面积为A，弹性模量为E。求杆的最大正应力及伸长。FqFF/1g=A1F12F.+△1 =dxEAEAFlFlFl2EA 2EAEA

8 第二章 拉伸、压缩与剪切 2.5 图示桁架ABC，在节点C承受集中载荷F作用。杆1与杆2的弹性模量均为E，横截面 面积分别为A1 = 2580 mm2 , A2 = 320 mm2。试问在节点B与C的位置保持不变的条件下，为 使节点C的铅垂位移最小，  应取何值(即确定节点A的最佳位置)。 F F FN2 FN1 C F FN2 FN1  C 1 l 2 l  解： FN1 = F cot, FN2 = F /sin  1 1 1 1 1 cot EA F l EA F l l N   = =  2 2 sin  cos 2 2 2 EA F l EA F l l N   = =       = +  +   =       tan cot sin cos 1 sin tan 2 1 2 2 1 E A A l l Fl CV = 0  d d CV 0 sin cos 8 cos 2 3 =        +    d d o  = 55.7 2.6 图示杆的横截面面积为 A，弹性模量为 E。求杆的最大正应力及伸长。 EA Fl EA Fl EA Fl dx EA x l F EA l F l A F l = + = +   = =  2 2 2 0 

第二章拉伸、压缩与剪切2.7图示硬铝试样，厚度8=2mm，试验段板宽b=20mm，标距/=70mm，在轴向拉力F=6kN的作用下，测得试验段伸长N/=0.15mm，板宽缩短△b=0.014mm，试计算硬铝的弹性模量E与泊松比μ。标距1十解：_FL_ 000×70 = 0.15E = 70000 MPaN=EA20×2EAb,_ 0.014/0.15 =0.327Au=b20702.8图示一阶梯形截面杆，其弹性模量E=200GPa，截面面积A/=300mm2A=250mm2,Am=200mm。试求每段杆的内力、应力、应变、伸长及全杆的总伸长

第二章 拉伸、压缩与剪切 9 2.7 图示硬铝试样，厚度  = 2mm ，试验段板宽b = 20 mm，标距l = 70 mm，在轴向拉 力F = 6kN的作用下，测得试验段伸长 l = 0.15mm ，板宽缩短 b = 0.014mm ，试计 算硬铝的弹性模量E与泊松比  。 解： 0.15 20 2 6000 70 =    = = EA E F l l N E = 70000 MPa =    l l b b / 0.327 70 0.15 / 20 0.014  = = 2.8 图示一阶梯形截面杆，其弹性模量 E=200GPa ， 截 面 面 积 AI=300mm2 ， AII=250mm2 ,AIII=200mm2。试求每段杆的内力、应力、应变、伸长及全杆的总伸长

10第二章 拉伸、压缩与剪切解：30kN15kN 10kN 25kNFNI =30kN,.1ml1.5m2mFNI30×103=100MPagi =A300×10-691_ 100×106=0.5×10-3=0.05%81=E200×109Nl = 8l = 0.5×10-3 ×1= 0.05mmFN215×103Fn2 =15kN,= 60MPa02250×10-6A260×10682=02= 0.3 ×10-3 = 0.03% 200×109EAl2 =82/ = 0.3×10-3×1.5=0.45mmFN325×103FN3 =25kN,= 125MPa03 =200×10-6A3125×10603= 0.625×10-3 = 0.0625%63E200×109Al;=83l3=0.625×10-3×2=1.25mmN/g = +N/ +/ =0.5 +0.45+1.25= 2.2mm2.9图示一三角架，在结点A受铅垂力F=20kN的作用。设杆AB为圆截面钢杆，直径d=8mm，杆AC为空心圆管，横截面面积为40×10~m2，二杆的E=200GPa。试求：结点A的位移值及其方向

10 第二章 拉伸、压缩与剪切 15kN 1m 2m 30kN 10kN 25kN 1.5m Ⅰ Ⅱ Ⅲ 15kN 1m 2m 30kN 10kN 25kN 1.5m Ⅰ Ⅱ Ⅲ 解： 1 N = 30kN , 3 1 1 6 1 30 10 100MPa 300 10 N A  −  = = =  6 1 3 1 9 100 10 0.5 10 0.05% E 200 10    − = = =  =  3 l l 1 1 1  0.5 10 1 0.05mm −  = =   = FN1 FN1 2 N =15kN , 3 2 2 6 2 15 10 60MPa 250 10 N A  −  = = =  6 2 3 2 9 60 10 0.3 10 0.03% E 200 10    − = = =  =  3 2 2 2 l l  0.3 10 1.5 0.45mm −  = =   = 3 N = 25kN , 3 3 3 6 3 25 10 125MPa 200 10 N A  −  = = =  6 3 3 3 9 125 10 0.625 10 0.0625% E 200 10    − = = =  =  3 l l 3 3 3  0.625 10 2 1.25mm −  = =   = 3 1 2 3  =  +  +  = + + = l l l l 0.5 0.45 1.25 2.2mm FN2 FN2 FN3 FN3 2.9 图示一三角架，在结点 A 受铅垂力 F = 20kN 的作用。设杆 AB 为圆截面钢杆，直径 d = 8mm，杆 AC 为空心圆管，横截面面积为 6 2 40 10 m −  ,二杆的 E = 200GPa。试求：结 点 A 的位移值及其方向

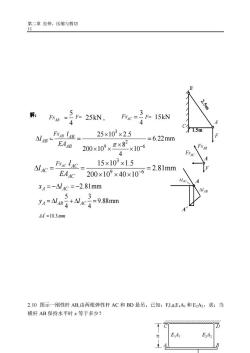
第二章拉伸、压缩与剪切35F解：F= 25kN,FNAC15kNFNAB425×103×2.5FNABIABNAR -=6.22mmEAAB200×109x元×82x10-6HNFNA15×10×1.5FNAc'"ACNAC=2.81mmEAAC200×10°×40×10-6XA=-NIAc =-2.81mm5+NAC=9.88mmYA=NABAAC4AA =10.3 mm2.10图示一刚性杆AB,由两根弹性杆AC和BD悬吊。已知：F,l,a,EiA:和E2A2，求：当横杆AB保持水平时×等于多少？E.A2E,A7

第二章 拉伸、压缩与剪切 11 1.5m C F A B 2.5m 解： 5 25kN , 4 N P AB = = 3 15kN 4 N P AC = = 3 2 9 6 25 10 2.5 6.22mm 8 200 10 10 4 AB AB AB AB N l l EA  −    = = =     3 9 6 15 10 1.5 2.81mm 200 10 40 10 AC AC AC AC N l l EA −    = = =    x l A AC = − = −2.81mm 5 3 9.88mm 4 4 A AB AC y l l =  +  = F A FNAB FNAC A A′ AC l AB l FN FNAB F= AC F= FNAB FNAC AA 10.3 mm ' = 2.10 图示一刚性杆 AB,由两根弹性杆 AC 和 BD 悬吊。已知：F,l,a,E1A1 和 E2A2，求：当 横杆 AB 保持水平时 x 等于多少？

12第二章 拉伸、压缩与剪切M-7p1L解：Fl-Fx=0IDCEA.E,A2F2/ -F(1-x)=0aFM2 =(-)p??B1FN ,=N2,FN4=FmFNFm.EAE24FE2Alx=EAE2A2E4+E2422.11一刚性杆AB,由三根长度相等的弹性杆悬吊。、①、杆的拉压刚度分别为EiA1、EzA2和EsA,结构受力如图所示。已知F、a、1，试求三杆内力

12 第二章 拉伸、压缩与剪切 解： x l E1A1 ① ② E2A2 A B C D a F FN1 FN2 A B F x 1 x N P l = 2 ( ) l x N P l − = 1 2  =  l l , 1 1 2 2 1 1 2 2 , N l N l E A E A = 1 1 2 2 , l x x P P l l E A E A − = 2 2 1 1 2 2 E A l x E A E A = + FN1 FN2 FN2 FN 0 1 FN1 l − Fx = FN2 l − F(l − x) = 0 F F 2.11 一刚性杆 AB,由三根长度相等的弹性杆悬吊。○1 、○2 、○3 杆的拉压刚度分别为 E1A1、 E2A2 和 E3A3,结构受力如图所示。已知 F、a、l，试求三杆内力