内蒙古科技大学：《材料力学》课程授课教案（讲义）第19讲 应力状态理论（Ⅰ）

材料力学教案第19讲教学方案应力状态理论（I）基本1.一点的应力状态。内2.主平面与主应力。容3.平面应力状态分析的解析法

材 料 力 学 教 案 第 19 讲 教学方案 —— 应力状态理论（Ⅰ） 基 本 内 容 1. 一点的应力状态。 2.主平面与主应力。 3.平面应力状态分析的解析法

讲第九T1.了解一点应力状态的基本概念,进行应力分析的意义。教学目的2．介绍平面应力状态的工程实例。3.掌握平面一般应力状态分析——解析法。的4．会应用解析法确定一点应力状态中的主应力、主方向、主剪应力、主剪平面方位及任意给定方位截面上的应力数值。5.对空间应力状态做简单介绍。1．重点掌握平面一般应力状态分析——解析法。重2.重点掌握主应力、主方向、主剪应力、主剪平面方位及任点意给定方位截面上的应力数值的计算方法。难3.理解一点应力状态的分析在构件强度计算中的重要作用。点难点是对构件危险点处的主应力、主方位客观存在的理4.解。本次教学计划学时：2学时。课堂讨论：教学1.材料的破坏与应力状态之间的关系。安2.不同性质的材料（塑性材料、脆性材料）在相同外力作用排下的破坏形式为什么不同？3.不同性质的材料（塑性材料、脆性材料）的机械性能（屈服滑移线、颈缩、断口等）与应力状态、材料的抗力性能的关系。4.从工程中实例指出单向、二向、三向应力状态危险点

第 十 九 讲 教 学 目 的 1. 了解一点应力状态的基本概念,进行应力分析的意义。 2. 介绍平面应力状态的工程实例。 3. 掌握平面一般应力状态分析——解析法。 4．会应用解析法确定一点应力状态中的主应力、主方向、主 剪应力、主剪平面方位及任意给定方位截面上的应力数值。 5．对空间应力状态做简单介绍。 重 点 、 难 点 1. 重点掌握平面一般应力状态分析——解析法。 2. 重点掌握主应力、主方向、主剪应力、主剪平面方位及任 意给定方位截面上的应力数值的计算方法。 3. 理解一点应力状态的分析在构件强度计算中的重要作用。 4. 难点是对构件危险点处的主应力、主方位客观存在的理 解。 教 学 安 排 本次教学计划学时：2 学时。 课堂讨论： 1. 材料的破坏与应力状态之间的关系。 2. 不同性质的材料（塑性材料、脆性材料）在相同外力作用 下的破坏形式为什么不同？ 3. 不同性质的材料（塑性材料、脆性材料）的机械性能（屈 服滑移线、颈缩、断口等）与应力状态、材料的抗力性能的关系。 4．从工程中实例指出单向、二向、三向应力状态危险点

材料力学教第七章应力状态理论s7-1一点应力状态概念1．凡提到“应力”，必须指明作用在哪一点，哪个（方向）截面上。因为受力构件内同一截面上不同点的应力一般是不同的，通过同一点不同（方向）截面上应力也是（a）弯曲架横截面上各点具有不同的正应力（b）弯曲梁横裁面上各点具有不同的剪应力图8-1不同的。例如，图8-1弯曲梁横截面上各点具有不同的正应力与剪应力；图8-2通过轴向拉伸杆件同一点m的不同（方向）截面上具有不同的应力。P(a)(b)图8-2轴向拉伸杆件同一点血的不同（方向）裁面上不同的应力2．一点处的应力状态是指通过一点不同截面上的应力情况，或指所有方位截面上应力的集合。应力分析就是研究这些不同方位截面上应力随截面方向的变化规律。如图8-3是通过轴向拉伸杆件内m点不同（方向）截面上的应力情况（集合）3：一点处的应力状态可用围绕该点截取的微单元体（微正六面体）上三对互相垂直微面上的应力情况来表示。如图8-4（ab）为轴向拉伸杆件内围绕m点截取的两种微元体。特点：根据材料的均匀连续假设，微元体（代表一个材料点）各微面上的应力均匀分布相互平行的两个侧面上应力大小相等、方向相反；互相垂直的两个侧面上剪应力服从剪切互等关系

材 料 力 学 教 案 第七章 应力状态理论 §7-1 一点应力状态概念 1． 凡提到“应力”，必须指明作用在哪一点，哪个（方向）截面上。因为受力构件内 同一截面上不同点的应力一般是不同的，通过同一点不同（方向）截面上应力也是 不同的。例如，图 8-1 弯曲梁横截面上各点具有不同的正应力与剪应力； 图 8-2 通过轴向拉伸杆件同一点 m 的不同（方向）截面上具有不同的应力。 ２．一点处的应力状态是指通过一点不同截面上的应力情况，或指所有方位截面上应力的集合。 应力分析就是研究这些不同方位截面上应力随截面方向的变化规律。如图 8-3 是通过轴向拉伸杆 件内 m 点不同（方向）截面上的应力情况（集合） ３．一点处的应力状态可用围绕该点截取的微单元体（微正六面体）上三对互相垂直微 面上的应力情况来表示。如图 8-4（a,b）为轴向拉伸杆件内围绕 m 点截取的两种微元体。 特点：根据材料的均匀连续假设，微元体（代表一个材料点）各微面上的应力均匀分布， 相互平行的两个侧面上应力大小相等、方向相反；互相垂直的两个侧面上剪应力服从剪切互 等关系

O-300--401s0Cv-0x/2Fo10500=003图8-3通过一点不同方向截面上应力的变化+459145°(a)(b)（a）沿横截面取的微元体（6）沿±45°面裁取的微元体图8-4*平面应力状态的工程实例1.薄壁圆筒压力容器D。为平均直径，8为壁厚由平衡条件=D-=0O, =PDa得轴向应力：(8-1a)48图8-5c（I-I，IⅡI-II为相距为B的横截面，H-H为水平径向面）2.球形贮气罐（图8-6）

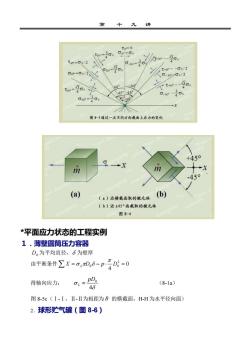
第 十 九 讲 *平面应力状态的工程实例 １．薄壁圆筒压力容器 D0 为平均直径，  为壁厚 由平衡条件 0 4 2 X = L D0 − p  D0 =     得轴向应力：   4 pD0 L = （8-1a） 图 8-5c（Ⅰ-Ⅰ，Ⅱ-Ⅱ为相距为 B 的横截面，H-H 为水平径向面） 2．球形贮气罐（图 8-6）

材料力学教察L由平衡条件ZY=sinadα-20,B=0或pBD。=20B8nB（a）承受内压力P的薄壁园简压力容器壁上一点m具有二向应力状态（b）求轴向应加L的受力图（I-I为横裁面）（c）求环向应力的受力图图8-5pD(8-1b)得环向应力：Cn=28由球对称知径向应力与纬向应力相同，设为α。对半球写平衡条件：。·元D8D·全+++PR(b)(a)图8-6求海壁原球经向与纬向应力的受力图得0=D(8-2)48

材 料 力 学 教 案 由平衡条件   = − =      0 0 sin 2 0 2 d B D Y pB H 或 pBD0 = 2 H B 得环向应力：   2 pD0 H = （8-1b） 由球对称知径向应力与纬向应力相同，设为  a 对半球写平衡条件： a  D = D  p 2 0 0 4     得   4 pD0 a = （8-2）

讲弯曲与扭转组合作用下的圆轴3.M(b)(a)(C)A-A横面受弯曲与扭转组①2两点和作用的国轴上的内力的应力状态图8-7受横向载荷作用的深梁4AAA（α）受模向力作用的深梁（b）回点的应力状态（h,L为同一量级）（平面一般应力状态）图8-8s7-2平面一般应力状态分析一解析法1.空间一般应力状态

第 十 九 讲 3． 弯曲与扭转组合作用下的圆轴 4． 受横向载荷作用的深梁 §7-2 平面一般应力状态分析——解析法 1．空间一般应力状态

学教索gx(b)(c)(a)空间一般应力状态平面一般应力状态平面一般应力状态的简化表示图 8-9如图8-9a所示，共有9个应力分量：x面上的w，g，T：J面上的m，Tw，ti=面上的otta1）应力分量的下标记法：第一个下标指作用面（以其外法线方向表示），第二个下标指作用方向。由剪应力互等定理，有：T, =t T =tyo t, =txo2）平乎面一般应力状态如图8-9b所示，即空间应力状态中，2方向的应力分量全部为零（o。=t=t,=0)；或只存在作用于x-y平面内的应力分量，,，Tg，Tg，其中o，,分别为，,的简写，而,=Tw3）正负号规定：正应力以拉应力为正，压为负；剪应力以对微元体内任意一点取矩为顺时针者为正，反之为负。2.平面一般应力状态斜截面上应力如图8-10所示，斜截面平行于z轴且与x面成倾角α，由力的平衡条件：Zn=0 和Zta=0可求得斜截面上应力α，Ta:Oα=0, cos'α+0, sin'α-T,-2sinαcosα(o, +0,)+(0±-0,)cos2α- ty sin 2α(8-3a)T, =(o, -0,)sin αcosα+T,(cos’α-sin’a)

材 料 力 学 教 案 如图 8-9a 所示，共有 9 个应力分量： x 面上的  xx ， xy  ， xz  ； y 面上的  yy ， yx  ， yz  ； z 面上的  zz， zx  ， zy  。 1）应力分量的下标记法：第一个下标指作用面（以其外法线方向表示），第二个下标指 作用方向。由剪应力互等定理，有： xy yx  =  ， yz zy  =  ， xz zx  =  。 2）平面一般应力状态如图 8-9b 所示，即空间应力状态中， z 方向的应力分量全部为 零（  zz =  zx =  zy = 0 ）；或只存在作用于 x-y 平面内的应力分量  x ， y ， xy  ， yx  ， 其中  x ， y 分别为  xx ， yy 的简写，而 xy  = yx  。 3）正负号规定：正应力以拉应力为正，压为负；剪应力以对微元体内任意一点取矩为 顺时针者为正，反之为负。 2．平面一般应力状态斜截面上应力 如图 8-10 所示，斜截面平行于 z 轴且与 x 面成倾角  ，由力的平衡条件： n = 0 和 t = 0 可求得斜截面上应力   ，   ：    cos   sin   2sin cos 2 2 = + −  x y xy   (  ) cos 2  sin 2 2 1 ( ) 2 1 = x + y + x − y − xy （8-3a） ( )sin cos (cos sin ) 2 2  xy =  x − y   + xy  − 

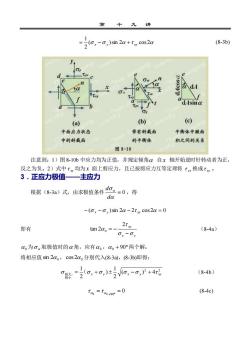
讲(8-3b),)sin2α+tmcos20ads三dAsina(c)(b)(a)带有斜裁面平街体中徽面平面应力状态中的斜裁面的平衡体积之间的关系图8-10注意到：1）图8-10b中应力均为正值，并规定倾角α自x轴开始逆时针转动者为正，反之为负。2）式中t均为x面上剪应力，且已按剪应力互等定理将t换成tm。主应力3.正应力极值根据（8-3a）式，由求极值条件do。α=0，得da-(α,-0,)sin 2α -2t cos2α = 02t,即有tan 2αg=(8-4a)a,-,α为。取极值时的α角，应有αo，α+90°两个解。将相应值sin2αg，cos2α分别代入(8-3a)，(8-3b)即得：(8-4b)(+0）V0）+4Ta = +90 = 0(8-4c)

第 十 九 讲 (  )sin 2  cos 2 2 1 = x − y + xy (8-3b) 注意到：1）图 8-10b 中应力均为正值，并规定倾角  自 x 轴开始逆时针转动者为正， 反之为负。2）式中 xy  均为 x 面上剪应力，且已按剪应力互等定理将 yx  换成 xy  。 3．正应力极值——主应力 根据（8-3a）式，由求极值条件 = 0    d d ，得 − ( x − y )sin 2 − 2 xy cos 2 = 0 即有 x y xy     − = − 2 tan 2 0 （8-4a）  0 为   取极值时的  角，应有  0 ， + 90  0 两个解。 将相应值 2 0 sin  ， 2 0 cos  分别代入(8-3a)，(8-3b)即得： 2 2 ( ) 4 2 1 ) 2 1 x y x y xy  = （ +   − +  极小 极大， （8-4b） 0 0 0 90 = = +      (8-4c)

材料力学教察说明：1）当倾角α转到α和α%+90°面时，对应有。，0ag+90，其中有一个为极大值，另一个为极小值；而此时ta，Ta+90均为零。可见在正应力取极值的截面上剪应力为零（如图8-1la)。Anda板小1+45°元100极大n+90o(b)(a)图8-112）定义：正应力取极值的面（或剪应力为零的面）为主平面，主平面的外法线方向称主方向，正应力的极值称主应力，对平面一般应力状态通常有两个非零主应力：极大，极小，故也称平面应力状态为二向应力状态。4.剪应力极值主剪应力根据(8-3b)式及取极值条件4f=0，可得：datan 2αg =,-0,(8-5a)2tayα为t。取极值时的α角，应有αg，α+90°两个解。将相应值sin2α，cos2α分别代入(8-3b)，(8-3a)即得：“w*“+Vo,-0,)+4r,-+(0ux一0u小)(8-5b)(极大+极小）=C a: =Qag+900

材 料 力 学 教 案 说明： 1）当倾角  转到  0 和 + 90  0 面时，对应有  0  ， +90 0  ，其中有一个为极大值，另 一个为极小值；而此时  0  ， +90  0  均为零。可见在正应力取极值的截面上剪应力为零（如 图 8-11a）。 2）定义：正应力取极值的面（或剪应力为零的面）为主平面，主平面的外法线方向称 主方向，正应力的极值称主应力，对平面一般应力状态通常有两个非零主应力：  极大 ， 极小 ， 故也称平面应力状态为二向应力状态。 4．剪应力极值——主剪应力 根据(8-3b)式及取极值条件 = 0    d d ，可得： xy x y     2 tan 2 * 0 − = （8-5a） *  0 为   取极值时的  角，应有 *  0 ， + 90 *  0 两个解。将相应值 * 2 0 sin  ， * 2 0 cos  分别代入 (8-3b)，(8-3a)即得： 极大 极小） 极小  极大，=   − +  =  ( − 2 1 ( ) 4 2 1 2 2 x y xy (8-5b)        = = + = +  ( 极大 极小） 2 1 90 * 0 * 0

讲九说明：1）当倾角α转到α和α℃+90°面时，对应有T极大，{极小，且二者大小均为（α楼大一〇楼小），方向相反，体现了剪应力互等定理，而此两面上正应力大小均取平均值（极天+の极小）（如图8-11b）。2）定义：剪应力取极值的面称主剪平面，该剪应力称主剪应力。注意到tan 2α -tan 2α. = -12α,= 2α±90°或α=α±45°因而主剪平面与主平面成±45°夹角

第 十 九 讲 说明：1）当倾角  转到 *  0 和 * 0  0 + 90 面时，对应有  极大 ， 极小 ，且二者大小均为 ( 极大 − 极小） 2 1 ，方向相反，体现了剪应力互等定理，而此两面上正应力大小均取平均值 ( 极大 + 极小） 2 1 （如图 8-11b）。 2）定义：剪应力取极值的面称主剪平面，该剪应力称主剪应力。注意到： tan 2 tan 2 0 1 *  0   = − 2 = 2  90 0 *  0  或 =  45 0 *  0  因而主剪平面与主平面成  45 夹角