内蒙古科技大学：《材料力学》课程授课教案（讲义）第16讲 提高弯曲强度的措施、薄壁截面的弯曲中心

材料力学教察第16讲教学方案提高弯曲强度的措施、薄壁截面的弯曲中心基本内容提高弯曲强度的若干措施、薄壁杆件的切应力流和弯曲中心。1、从弯曲强度条件出发，掌握提高弯曲强度的若干措施。2、理解等强度梁的概念。教学3、确定薄壁杆件切应力流的方向。目的理解弯曲中心对开口薄壁杆件的重要性，掌握确定弯曲中心的方法。重点本节重点：提高弯曲强度的若干措施。、难点本节难点：确定弯曲中心

材 料 力 学 教 案 1 第 16 讲 教学方案 ——提高弯曲强度的措施、薄壁截面的弯曲中心 基 本 内 容 提高弯曲强度的若干措施、薄壁杆件的切应力流和弯曲中心。 教 学 目 的 1、从弯曲强度条件出发，掌握提高弯曲强度的若干措施。 2、理解等强度梁的概念。 3、确定薄壁杆件切应力流的方向。 4、理解弯曲中心对开口薄壁杆件的重要性，掌握确定弯曲中心的方 法。 重 点 、 难 点 本节重点：提高弯曲强度的若干措施。 本节难点：确定弯曲中心

讲六sS5-5提高弯曲强度的措施如前所述，弯曲正应力是影响弯曲强度的主要因素。根据弯曲正应力的强度条件M≤[0](a)mxW.上式可以改写成内力的形式(b)Mmx≤[M]=W.[o]（b）式的左侧是构件受到的最大弯矩，（b）式的右侧是构件所能承受的许用弯矩由（a）和（b）两式可以看出，提高弯曲强度的措施主要是从三方面考虑：减小最大弯矩、提高抗弯截面系数和提高材料的力学性能。1.减小最大弯矩1）改变加载的位置或加载方式人和AT首先，可以通过改变加载位置或加载方式达到减小最大弯矩的目的。如当集中力作用在简支梁跨度中间时（6-13a），其最大弯矩为PI：当载荷的作用点移到梁的一侧，如距(a)副左侧=1处（图6-13b），则最大弯矩变为七+专+#P1，是原最大弯矩的0.56倍。当载荷的-P位置不能改变时，可以把集中力分散成较小的力，或者改变成分布载荷，从而减小最大弯矩。例如利用副梁把作用于跨中的集中力分散为(c)b)两个集中力（图6-13c），而使最大弯矩降低为图6-13改变加载的位置或加载方式以减小最大弯矩Pl。利用副梁来达到分散载荷，减小最大弯矩是工程中经常采用的方法。2）改变支座的位置其次，可以通过改变支座的位置来减小最大弯矩。例如图6-14a所示受均布载荷的简支梁，Mmxql2=0.125ql2。若将两端支座各向里移动0.21（图6-14b)，则最大弯矩减小为40932

第 十 六 讲 2 §5-5 提高弯曲强度的措施 如前所述，弯曲正应力是影响弯曲强度的主要因素。根据弯曲正应力的强度条件 [ ] max  max =   Wz M （a） 上式可以改写成内力的形式 [ ] [ ] Mmax  M = Wz  （b） （b）式的左侧是构件受到的最大弯矩，（b）式的右侧是构件所能承受的许用弯矩。 由（a）和（b）两式可以看出，提高弯曲强度的措施主要是从三方面考虑：减小最大弯 矩、提高抗弯截面系数和提高材料的力学性能。 1．减小最大弯矩 1）改变加载的位置或加载方式 首先，可以通过改变加载位置或加载方式 达到减小最大弯矩的目的。如当集中力作用在 简支梁跨度中间时（6-13a），其最大弯矩为 Pl 4 1 ；当载荷的作用点移到梁的一侧，如距 左侧 l 6 1 处（图 6-13b ），则最大弯矩变为 Pl 36 5 ，是原最大弯矩的 0.56 倍。当载荷的 位置不能改变时，可以把集中力分散成较小的 力，或者改变成分布载荷，从而减小最大弯矩。 例如利用副梁把作用于跨中的集中力分散为 两个集中力（图 6-13c）,而使最大弯矩降低为 Pl 8 1 。利用副梁来达到分散载荷，减小最大 弯矩是工程中经常采用的方法。 2）改变支座的位置 其次，可以通过改变支座的位置来减小最大弯矩。例如图 6-14a 所示受均布载荷的简支 梁， 2 2 max 0.125 8 1 M = ql = ql 。若将两端支座各向里移动 0.2l （图 6-14b），则最大弯矩减 小为 2 40 1 ql

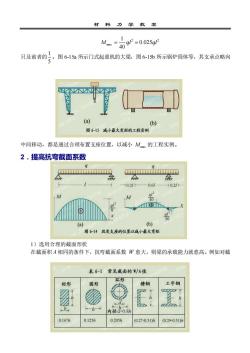
材料力学教察Mm = qr =0.025grp只及前者的。图6-15a所示门式起重机的大梁，图6-15b所示锅炉简体等，其支承点略向NH(a)(b)图 6-15 减小最大变矩的工程实例中间移动，都是通过合理布置支座位置，以减小M的工程实例。2.提高抗弯截面系数更发M开分0210.210.6MO(b)(a)图 6-14 改变支座的位置以减小最大考矩1）选用合理的截面形状在截面积A相同的条件下，抗弯截面系数W愈大，则梁的承载能力就愈高。例如对截表6-1常见裁面的W/A值环形工字钢矩形槽钢圆形内径80.167A0.125h0.205h(0.27-0.31）万(0.29-0.31)

材 料 力 学 教 案 3 2 2 max 0.025 40 1 M = ql = ql 只及前者的 5 1 。图 6-15a 所示门式起重机的大梁，图 6-15b 所示锅炉筒体等，其支承点略向 中间移动，都是通过合理布置支座位置，以减小 Mmax 的工程实例。 2．提高抗弯截面系数 1）选用合理的截面形状 在截面积 A 相同的条件下，抗弯截面系数 W 愈大，则梁的承载能力就愈高。例如对截

面高度h大于宽度b的矩形截面梁，梁竖放时W，=bh2；而梁平放时，W,hb2。两者之比是※=么>1，所以竖放比平放有较高的抗弯能力。当截面的形状不同时，可以用比值兴来衡量截面形状的合理性和经济性。常见截面的兴值列于表6-1中。表中的数据表明，材料远离中性轴的截面（如圆环形、工字形等）比较经济合理。这是因为弯曲正应力沿截面高度线性分布，中性轴附近的应力较小，该处的材料不能充分发挥作用，将这些材料移置到离中性轴较远处，则可使它们得到充分利用，形成“合理截面”。工程中的吊车梁、桥梁常采用工字形、槽形或箱形截面，房屋建筑中的楼板采用空心圆孔板，道理就在于此。需要指出的是，对于矩形，工字形等截面，增加截面高度虽然能有效地提高抗弯截面系数；但若高度过大，宽度过小，则在载荷作用下梁会发生扭曲，从而使梁过早的丧失承载能力。对于拉、压许用应力不相等的材料（例如大多数脆性材料），采用T字形等中性轴距上下边不相等的截面较合理。设计时使中性轴靠近拉应力的一侧，以使危险截面上的最大拉应力和最大压应力尽可能同时达到材料的许用应力。2）用变截面梁对于等截面梁，除M所在截面的最大正应力达到材料的许用应力外，其余截面的应力均小于，甚至远小于许用应力。因此，为了节省材料，减轻结构的格重量，可在弯矩较小处采用较小的截面，这种截面尺寸沿梁轴线变化(a)的梁称为变截面梁。若使变截面梁每个截面上的最大正应力都等于材TA料的许用应力，则这种梁称为等强度梁。考虑到加工的经济性及其他(b)(c)工艺要求，工程实际中只能作成近图6-16变裁面梁的工程实例似的等强度梁，例如机械设备中的阶梯轴（图6-16a)，摇臂钻床的摇臂（图6-16c）及工业厂房中的鱼腹梁（图6-16b）等。3.提高材料的力学性能构件选用何种材料，应综合考虑安全、经济等因素。近年来低合金钢生产发展迅速，如16Mn、15MnTi钢等。这些低合金钢的生产工艺和成本与普通钢相近，但强度高、韧性好。南京长

第 十 六 讲 4 面高度 h 大于宽度 b 的矩形截面梁，梁竖放时 2 1 6 1 W = bh ；而梁平放时， 2 2 6 1 W = hb 。两者 之比是 1 2 1 =  b h W W ，所以竖放比平放有较高的抗弯能力。当截面的形状不同时，可以用比值 A W 来衡量截面形状的合理性和经济性。常见截面的 A W 值列于表 6-1 中。 表中的数据表明，材料远离中性轴的截面（如圆环形、工字形等）比较经济合理。这是 因为弯曲正应力沿截面高度线性分布，中性轴附近的应力较小，该处的材料不能充分发挥作 用，将这些材料移置到离中性轴较远处，则可使它们得到充分利用，形成“合理截面”。工 程中的吊车梁、桥梁常采用工字形、槽形或箱形截面，房屋建筑中的楼板采用空心圆孔板， 道理就在于此。需要指出的是，对于矩形，工字形等截面，增加截面高度虽然能有效地提高 抗弯截面系数；但若高度过大，宽度过小，则在载荷作用下梁会发生扭曲，从而使梁过早的 丧失承载能力。 对于拉、压许用应力不相等的材料（例如大多数脆性材料），采用 T 字形等中性轴距上 下边不相等的截面较合理。设计时使中性轴靠近拉应力的一侧，以使危险截面上的最大拉应 力和最大压应力尽可能同时达到材料的许用应力。 2）用变截面梁 对于等截面梁，除 Mmax 所在截面的最大正应力达到材料的许用应力外，其余截面的应 力均小于，甚至远小于许用应力。 因此，为了节省材料，减轻结构的 重量，可在弯矩较小处采用较小的 截面，这种截面尺寸沿梁轴线变化 的梁称为变截面梁。若使变截面梁 每个截面上的最大正应力都等于材 料的许用应力，则这种梁称为等强 度梁。考虑到加工的经济性及其他 工艺要求，工程实际中只能作成近 似的等强度梁，例如机械设备中的 阶梯轴（图 6-16a），摇臂钻床的摇 臂（图 6-16c）及工业厂房中的鱼腹梁（图 6-16b）等。 3．提高材料的力学性能 构件选用何种材料，应综合考虑安全、经济等因素。近年来低合金钢生产发展迅速，如 16Mn 、 15MnTi 钢等。这些低合金钢的生产工艺和成本与普通钢相近，但强度高、韧性好。南京长

费店江大桥广泛的采用了16Mn钢，与低碳钢相比节约了15%的钢材。铸铁抗拉强度较低，但价格低廉。铸铁经球化处理成为球墨铸铁后，提高了强度极限和塑性性能。不少工厂用球墨铸铁代替钢材制造曲轴和齿轮，取得了较好的经济效益。$5-6薄壁截面的弯曲中心对于薄壁截面梁，若横向力作用在纵向对称面内，梁将发生平面弯曲。若横向力没作用在对称平面内，则力必须通过截面上某一特定的点，该点称为弯典虫心，且平行于形心主轴时，梁才能发生平面弯曲。否则，梁在发生弯曲的同时，还将发生扭转。确定弯曲中心的方法是，先假定在横向力作用下梁发生平面弯曲，研究此时横截面上的剪应力分布，求出剪应力的合力作用点，此即弯曲中心。再根据内外力的关系，确定产生平面弯曲的加载条件。-b-(a)(c)(b)图6-10薄壁截面的水平剪应力现以图示的槽形截面悬臂梁为例，说明确定弯曲中心的方法。设横向力P通过点A.且平行于形心主轴y，梁发生平面弯曲而没有扭转（6-10a)。此时梁的横截面上不但有正应力，还有剪应力。除腹板上有垂直剪应力外，在翼缘上还将产生水平剪应力。由于翼缘很薄，对水平剪应力T，同样假定：（1）剪应力平行于翼缘的周边，（2）沿翼缘厚度均匀分布（图6-10b)。为了分析水平剪应力，以相距为dx的两横截面及垂直于翼缘中线的纵截面自翼缘上截取一微段，微段横截面上作用有正应力的合力N,、N2，在截开的纵截面上作用有剪应力T（图6-10c)。其中

材 料 力 学 教 案 5 江大桥广泛的采用了 16Mn 钢，与低碳钢相比节约了 15% 的钢材。铸铁抗拉强度较低，但价 格低廉。铸铁经球化处理成为球墨铸铁后，提高了强度极限和塑性性能。不少工厂用球墨铸 铁代替钢材制造曲轴和齿轮，取得了较好的经济效益。 §5-6 薄壁截面的弯曲中心 对于薄壁截面梁，若横向力作用在纵向对称面内，梁将发生平面弯曲。若横向力没作用在对 称平面内，则力必须通过截面上某一特定的点，该点称为弯曲中心，且平行于形心主轴时，梁才 能发生平面弯曲。否则，梁在发生弯曲的同时，还将发生扭转。 确定弯曲中心的方法是，先假定在横向力作用下梁发生平面弯曲，研究此时横截面上的剪应 力分布，求出剪应力的合力作用点，此即弯曲中心。再根据内外力的关系，确定产生平面弯曲的 加载条件。 现以图示的槽形截面悬臂梁为例，说明确定弯曲中心的方法。设横向力 P 通过点 A ， 且平行于形心主轴 y，梁发生平面弯曲而没有扭转（6-10a）。此时梁的横截面上不但有正应力， 还有剪应力。除腹板上有垂直剪应力外，在翼缘上还将产生水平剪应力。由于翼缘很薄，对水平 剪应力 1  同样假定：（1）剪应力平行于翼缘的周边，（2）沿翼缘厚度均匀分布（图 6-10b）。为 了分析水平剪应力，以相距为 dx 的两横截面及垂直于翼缘中线的纵截面自翼缘上截取一微段， 微段横截面上作用有正应力的合力 N1 、N2 ，在截开的纵截面上作用有剪应力  ' （图 6-10c）。 其中

六L.MdAN,=JMN -I, i+aya1根据剪应力成对定理和微段沿x方向的平衡条件x=0，有N,-N,-Ttdx=0Ti = t'= OS"得(a)水平剪应力的计算公式与腹板上垂直剪应力的计算0公式完全相同，式中S:=tu，可见水平剪应力沿翼缘线性分布。同样可求出下翼缘上水平剪应力的方向与分布规律。由图6-11a可以看出，剪应力沿截面中线形成“剪流”裁面剪应力的分布图6-11格及宽心的确上翼缘水平剪应力的合力[" Ohu du- Ob"mO - I titdu= (b)02141.下翼缘水平剪应力的合力Q,=Q，但与Q,的方向相反；腹板垂直剪应力的合力O,=Q（图6-11b)。根据合力之矩定理，9、Q,和O,的合力作用点应在距腹板中线为e的A点处。e=h_hb(c)041.若横向力通过A点，截面上的剪力Q与外力形成的力偶矢量平行于=轴，使梁发生平面弯曲。若外力不通过A点，则外力与截面上的剪力Q不在同一纵向面内，将外力向A点平移后，附加的力偶将使梁发生扭转变形。所以弯曲中心是平面弯曲时横截面上剪应力的合力作用点。由式（c）可以看出，弯曲中心的位置只取决于截面的形状和尺寸，而与外力无关。弯曲中心简称为弯心，当截面有两个对称轴时，两个对称轴的交点即为弯曲中心，此时弯曲中心与形心重合，如工字形截面。当截面有一个对称轴时，可假定外力垂直于该对称轴，并产生平面弯曲，求6

第 十 六 讲 6 ( ) dA I M dM y N dA I My N A z A z   + = = * * 2 1 根据剪应力成对定理和微段沿 x 方向的平衡条件 x = 0 ，有 N2 − N1 −'tdx = 0 得 z tI QS * 1  =  ' = （a） 水平剪应力的计算公式与腹板上垂直剪应力的计算 公式完全相同，式中 tu h Sz 2 * = ，可见水平剪应力沿 翼缘线性分布。同样可求出下翼缘上水平剪应力的 方向与分布规律。由图 6-11a 可以看出，剪应力沿 截面中线形成“剪流”。 上翼缘水平剪应力的合力 z b z b I Qb ht du I Qhut Q tdu 2 4 2 0 0 1 = 1 = =    （b） 下翼缘水平剪应力的合力 Q2 = Q1 ，但与 Q1 的方向相反；腹板垂直剪应力的合力 Q3 = Q （图 6-11b）。根据合力之矩定理， Q1 、Q2 和 Q3 的合力作用点应在距腹板中线为 e 的 A 点处。 z I h b t Q Q h e 4 2 2 1 = = (c) 若横向力通过 A 点，截面上的剪力 Q 与外力形成的力偶矢量平行于 z 轴，使梁发生平面弯 曲。若外力不通过 A 点，则外力与截面上的剪力 Q 不在同一纵向面内，将外力向 A 点平 移后，附加的力偶将使梁发生扭转变形。 所以弯曲中心是平面弯曲时横截面上剪应力的合力作用点。由式（c）可以看出，弯曲 中心的位置只取决于截面的形状和尺寸，而与外力无关。弯曲中心简称为弯心。 当截面有两个对称轴时，两个对称轴的交点即为弯曲中心，此时弯曲中心与形心重合， 如工字形截面。当截面有一个对称轴时，可假定外力垂直于该对称轴，并产生平面弯曲，求

材料力学教案力#学得截面上剪应力合力的作用线，该作用线与对称轴的交点即为弯曲中心，此时弯曲中心一般与形心不重合，如槽形截面。对于没有对称轴的薄壁截面应这样求弯曲中心：（1）确定形心主轴。（2）设横向力平行于某一形心主轴，并使梁产生平面弯曲，求出截面上弯曲剪应力合力作用线的位置。（3）设横向力平行于另一形心主轴，并使梁产生平面弯曲，求出对于此平面弯曲截面上剪应力合力作用线的位置。（4）两合力作用线的交点即为弯曲中心的位置。对于形状较简单的薄壁截面，根据弯心的概念和剪流的特点，可以很快定出弯心的位置如6-12所示。对于实心截面杆，由于忽略剪应力的影响，故认为弯心与形心重合。开口薄壁截面杆的抗扭刚度较小，如横向力不A通过弯曲中心，将引起比较严重的扭转变形，不但要产生扭转剪应力，有时还将因约束扭转而引起附?(6)(c)加的正应力和剪应力。对这类杆件进行强度计算时，图 6-12 根据剪流确定弯心的位置对弯曲中心的问题应予以足够的重视。本章小结1.受弯构件横截面上有两种内力一一弯矩和剪力。弯矩M在横截面上产生正应力；剪力○在横截面上产生剪应力2．已知横截面上的内力，求横截面上的应力属于静不定问题，必须利用变形关系、物理关系和静力平衡关系。弯矩产生的正应力是影响强度和刚度的主要因素，故对弯曲正应力进行了较严格的推导。剪力产生的剪应力对梁的强度和刚度的影响是次要因素，故对剪应力公式没作严格推导，先假定了剪应力的分布规律，然后用平衡关系直接求出剪应力的计算公式。3.梁进行强度计算时，主要是满足正应力的强度条件_ M ≤[0]OmexW某些特殊情况下，还要校核是否满足剪应力的强度条件7

材 料 力 学 教 案 7 得截面上剪应力合力的作用线，该作用线与对称轴的交点即为弯曲中心，此时弯曲中心一般 与形心不重合，如槽形截面。对于没有对称轴的薄壁截面应这样求弯曲中心： （1）确定形心主轴。 （2）设横向力平行于某一形心主轴，并使梁产生平面弯曲，求出截面上弯曲剪应力合 力作用线的位置。 （3）设横向力平行于另一形心主轴，并使梁产生平面弯曲，求出对于此平面弯曲截面 上剪应力合力作用线的位置。 （4）两合力作用线的交点即为弯曲中心的位置。 对于形状较简单的薄壁截面，根据弯心的概念和剪流的特点，可以很快定出弯心的位置， 如 6-12 所示。 对于实心截面杆，由于忽略剪应力的影响，故 认为弯心与形心重合。 开口薄壁截面杆的抗扭刚度较小，如横向力不 通过弯曲中心，将引起比较严重的扭转变形，不但 要产生扭转剪应力，有时还将因约束扭转而引起附 加的正应力和剪应力。对这类杆件进行强度计算时， 对弯曲中心的问题应予以足够的重视。 本章小结 1．受弯构件横截面上有两种内力——弯矩和剪力。弯矩 M 在横截面上产生正应力  ；剪 力 Q 在横截面上产生剪应力  。 2．已知横截面上的内力，求横截面上的应力属于静不定问题，必须利用变形关系、物理关 系和静力平衡关系。 弯矩产生的正应力是影响强度和刚度的主要因素，故对弯曲正应力进行了较严格的推导。剪 力产生的剪应力对梁的强度和刚度的影响是次要因素，故对剪应力公式没作严格推导，先假定了 剪应力的分布规律，然后用平衡关系直接求出剪应力的计算公式。 3．梁进行强度计算时，主要是满足正应力的强度条件 [ ] max  max =   Wz M 某些特殊情况下，还要校核是否满足剪应力的强度条件

讲第六_ 0m (S) m= ≤[1])Tmexbl.4．根据强度条件表达式，提高构件弯曲强度的主要措施是：减小最大弯矩；提高抗弯截面系数和材料性能。5．弯曲中心是薄壁截面横弯时，横截面上剪应力的合力作用点。因此横弯作用的薄壁截面梁，发生平面弯曲的充要条件是：1）横向载荷过弯曲中心；2）平行于形心主轴。8

第 十 六 讲 8 [ ] ( )max * max max  =   z z bI Q S 4．根据强度条件表达式，提高构件弯曲强度的主要措施是：减小最大弯矩；提高抗弯截面 系数和材料性能。 5．弯曲中心是薄壁截面横弯时，横截面上剪应力的合力作用点。因此横弯作用的薄壁截面 梁，发生平面弯曲的充要条件是： 1）横向载荷过弯曲中心； 2）平行于形心主轴