内蒙古科技大学：《材料力学》课程授课教案（讲义）第13讲 弯曲内力（Ⅱ）

材料力学教案第13讲教学方案弯曲内力（I)基本内容利用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯矩图。1、掌握载荷集度、剪力和弯矩间的微分关系。2、理解集中力和集中力偶处剪力图和弯矩图的突变现象及其真正含教学+目的3、熟练利用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯矩图。重点本节重点：利用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯矩图。、难点本节难点：载荷集度、剪力和弯矩之间的微分关系的理解

材 料 力 学 教 案 1 第 13 讲 教学方案 ——弯曲内力(Ⅱ) 基 本 内 容 利用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯矩图。 教 学 目 的 1、掌握载荷集度、剪力和弯矩间的微分关系。 2、理解集中力和集中力偶处剪力图和弯矩图的突变现象及其真正含 义。 3、熟练利用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯矩 图。 重 点 、 难 点 本节重点：利用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯 矩图。 本节难点：载荷集度、剪力和弯矩之间的微分关系的理解

s4-4载荷集度剪力和弯矩间的微分关系考察图5-7a所示承受任意载荷的梁。从梁上受分布载荷的段内截取dx微段，其受力如图5-7b所示。作用在微段上的分布载荷可以认为是均布的，十价并设向上为正。微段两侧截面上的内力均设为正方(a)向。若x截面上的内力为Q(x)、M(x)，则x+dx截面上的内力为Q(x)+do(x)、M(x)+dM(x)。因为梁整体是平衡的，dx微段也应处于平衡。根据平衡条件Zy=0和m。=0，得到(b)a图 5-7 受分布载荷的微段梁的平衡Q(x)+q(x)dx-(Ox)+ dQ(x) =0d=0M(x)+dM(x)-M(x)-Q(x)dx-q(x)略去其中的高阶微量后得到d0(α) = q(x)(5-1)dxdM(x) =Q(x)(5-2)dx利用式（5-1）和（5-2）可进一步得出d M(a = g(x)(5-3)dx式（5-1）、（5-2）和（5-3）是剪力、弯矩和分布载荷集度9之间的平衡微分关系，它表明：1．剪力图上某处的斜率等于梁在该处的分布载荷集度α。2，弯矩图上某处的斜率等于梁在该处的剪力。3．弯矩图上某处的斜率变化率等于梁在该处的分布载荷集度q根据上述微分关系，由梁上载荷的变化即可推知剪力图和弯矩图的形状。例如：1.若某段梁上无分布载荷，即g(x)=0，则该段梁的剪力Q(x)为常量，剪力图为平行于x轴的直线；而弯矩M(x)为x的一次函数，弯矩图为斜直线2

第 十 三 讲 2 §4-4 载荷集度 剪力和弯矩间的微分关系 考察图 5-7a 所示承受任意载荷的梁。从梁上受 分布载荷的段内截取 dx 微段，其受力如图 5-7b 所 示。作用在微段上的分布载荷可以认为是均布的， 并设向上为正。微段两侧截面上的内力均设为正方 向。若 x 截面上的内力为 Q(x) 、M (x) ，则 x + dx 截面上的内力为 Q(x) + dQ(x)、 M (x) + dM (x) 。 因为梁整体是平衡的， dx 微段也应处于平衡。根据 平衡条件 y = 0 和 mo = 0 ，得到 0 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )) 0 2 + − − − = + − + = dx M x dM x M x Q x dx q x Q x q x dx Qx dQ x 略去其中的高阶微量后得到 ( ) ( ) q x dx dQ x = （5-1） ( ) ( ) Q x dx dM x = (5-2） 利用式（5-1）和（5-2）可进一步得出 ( ) ( ) 2 2 q x dx d M x = （5-3） 式（5-1）、（5-2）和（5-3）是剪力、弯矩和分布载荷集度 q 之间的平衡微分关系，它 表明： １．剪力图上某处的斜率等于梁在该处的分布载荷集度 q 。 ２．弯矩图上某处的斜率等于梁在该处的剪力。 ３．弯矩图上某处的斜率变化率等于梁在该处的分布载荷集度 q 。 根据上述微分关系，由梁上载荷的变化即可推知剪力图和弯矩图的形状。例如： １．若某段梁上无分布载荷，即 q(x) = 0 ，则该段梁的剪力 Q(x) 为常量，剪力图为平 行于 x 轴的直线；而弯矩 M (x) 为 x 的一次函数，弯矩图为斜直线

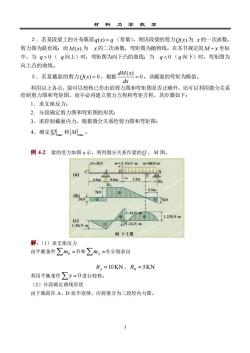
材料力学教索2。若某段梁上的分布载荷q(x)=α（常量)，则该段梁的剪力Q(n)为x的一次函数剪力图为斜直线；而M(x)为x的二次函数，弯矩图为抛物线。在本书规定的M-x坐标中，当q>0（q向上）时，弯矩图为向下凸的曲线；当q<0（q向下）时，弯矩图为向上凸的曲线。3.若某截面的剪力0()=0，根据AM(=0，该截面的弯矩为极值。dx利用以上各点，除可以校核已作出的剪力图和弯矩图是否正确外，还可以利用微分关系绘制剪力图和弯矩图，而不必再建立剪力方程和弯矩方程，其步骤如下：1.求支座反力；2.．分段确定剪力图和弯矩图的形状；3．求控制截面内力，根据微分关系绘剪力图和弯矩图；4.确定9lm和Mmx。例4-2梁的受力如图a示，利用微分关系作梁的O、M图P=3KNm=3.6kN-B(a)A06m个06m12m20.5m7kNknuenCESLNRl/1.2k.mLSKN·TI例5-2图解：（1）求支座反力由平衡条件mg=0和m^=0分别求出R =10KN, R =5KN利用平衡条件y=0进行校核。（2）分段确定曲线形状由于载荷在A、D处不连续，应将梁分为三段绘内力图。3

材 料 力 学 教 案 3 ２．若某段梁上的分布载荷 q(x) = q （常量），则该段梁的剪力 Q(x) 为 x 的一次函数， 剪力图为斜直线；而 M (x) 为 x 的二次函数，弯矩图为抛物线。在本书规定的 M − x 坐标 中，当 q  0 （ q 向上）时，弯矩图为向下凸的曲线；当 q  0 （ q 向下）时，弯矩图为 向上凸的曲线。 ３．若某截面的剪力 Q(x) = 0 ，根据 0 ( ) = dx dM x ，该截面的弯矩为极值。 利用以上各点，除可以校核已作出的剪力图和弯矩图是否正确外，还可以利用微分关系 绘制剪力图和弯矩图，而不必再建立剪力方程和弯矩方程，其步骤如下： 1．求支座反力； 2．分段确定剪力图和弯矩图的形状； 3．求控制截面内力，根据微分关系绘剪力图和弯矩图； 4．确定 max Q 和 M max 。 例 4-2 梁的受力如图 a 示，利用微分关系作梁的 Q 、 M 图。 解：（1）求支座反力 由平衡条件 mB = 0 和 mA = 0 分别求出 RA =10KN ， RB = 5KN 利用平衡条件 y = 0 进行校核。 （2）分段确定曲线形状 由于载荷在 A、D 处不连续，应将梁分为三段绘内力图

讲第==O和M根据微分关系dM=9，CA和AD段内，g=0，剪力图为水平=qdxdx?dx线，弯矩图为斜直线；DB段内，q=常数，且为负值，剪力为斜直线，M图为向上凸的抛物线。（3）求控制截面的内力值，绘Q、M图Q图：Qc右=-3KN，Q诺=7KN，据此可作出CA和AD两段Q图的水平线。QD右=7KN，Q左=-5KN，据此作出DB段Q图的斜直线。M图：Mc=0，MA左=-1.8KN·m，据此可以作出CA段弯矩图的斜直线。A支座的约束反力R。只会使截面A左右两侧剪力发生突变，不改变两侧的弯矩值，故MA左=MA右=M,=-1.8KNm，MD左=2.4KN.m，据此可作出AD段弯矩图的斜直线。D处的集中力偶会使D截面左右两侧的弯矩发生突变,故需求出Mp右=-1.2KN-m，M==0由DB段的剪力图知在E处Q=0，该处弯矩为极值。因R=5KN，根据BE段的平衡条件y=0，知BE段的长度为0.5m，于是求得Mg=1.25KNm。根据上述三个截面的弯矩值可作出DB段的M图。对作出的Q、M图要利用微分关系和突变规律、端点规律作进一步的校核。如DB段内的均布载荷为负值，该段O图的斜率应为负：CA段的O为负值，该段M图的斜率应为负：AD段的Q为正值，该段M图的斜率应为正：支座A处剪力图应发生突变，突变值应为10KN：D处有集中力偶，D截面左右两侧的弯矩应发生突变，而且突变值应为3.6KN-m；支座B和自由端C处的弯矩应为零等

第 十 三 讲 4 根据微分关系 q dx dQ = 、 Q dx dM = 和 q dx d M = 2 2 ，CA 和 AD 段内， q = 0 ，剪力图为水平 线，弯矩图为斜直线；DB 段内， q =常数 ，且为负值，剪力 为斜直线， M 图为向上凸的抛物 线。 （3）求控制截面的内力值，绘 Q 、 M 图 Q 图： QC右 = −3KN ， QA右 = 7KN ，据此可作出 CA 和 AD 两段 Q 图的水平线。 QD右 = 7KN，QB左 = −5KN ，据此作出 DB 段 Q 图的斜直线。 M 图： MC = 0， M A左 = −1.8KNm ，据此可以作出 CA 段弯矩图的斜直线。A 支座的 约束反力 RA 只会使截面 A 左 右 两 侧 剪 力 发 生 突 变 ， 不 改 变 两 侧 的 弯 矩 值 ， 故 M A左 = M A右 = M A = −1.8KNm ，MD左 = 2.4KNm ，据此可作出 AD 段弯矩图的斜直线。 D处的集中力偶会使D截面左右两侧的弯矩发生突变，故需求出 MD右 = −1.2KNm ，MB = 0 ； 由 DB 段的剪力图知在 E 处 Q = 0 ，该处弯矩为极值。因 RB = 5KN ，根据 BE 段的平衡条件 y = 0 ，知 BE 段的长度为 0.5m，于是求得 ME =1.25KNm 。根据上述三个截面的弯矩值 可作出 DB 段的 M 图。 对作出的 Q 、 M 图要利用微分关系和突变规律、端点规律作进一步的校核。如 DB 段内的均布 载荷为负值，该段 Q 图的斜率应为负；CA 段的 Q 为负值，该段 M 图的斜率应为负；AD 段的 Q 为正值，该段 M 图的斜率应为正；支座 A 处剪力图应发生突变，突变值应为 10KN；D 处有集 中力偶，D 截面左右两侧的弯矩应发生突变，而且突变值应为 3.6KNm；支座 B 和自由端 C 处 的弯矩应为零等