内蒙古科技大学：《材料力学》课程教学资源（习题解答）应力状态分析和强度理论

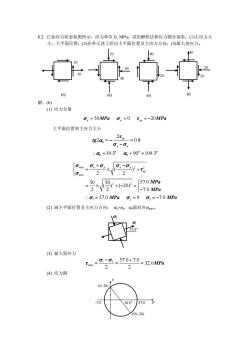
8.2.已知应力状态如图所示，应力单位为MPa。试用解析法和应力圆分别求：（1)主应力大小，主平面位置；(2)在单元体上绘出主平面位置及主应力方向：(3)最大切应力。2080430(e)解： (b)(1)应力分量,=50MPa ,=0=-20MPa主平面位置和主应力大小2t.=0.8tg2αga,-,.%=19.3°α+90°=109.3°fomax_a,+a,or-ory+tCJ57.0 MPa-+/g(-20 -{-7.0 MPa..0, = 57.0 MPa, =-7.0 MPa=(2）画主平面位置及主应力方向：>0y，α0面对应0ma1019(3)最大剪应力_g-0;_ 570+70 =32.0MPa(4)应力圆

8.2. 已知应力状态如图所示，应力单位为 MPa。试用解析法和应力圆分别求：(1)主应力大 小，主平面位置；(2)在单元体上绘出主平面位置及主应力方向；(3)最大切应力。 20 80 (e) 20 30 (f) 20 20 50 (b) 40 40 (d) 20 解：(b) (1) 应力分量 50 0 20 σ x yx = == MPa σ τ y − MPa 主平面位置和主应力大小 0 0 0 2 2 0.8 19.3 90 109.3 xy x y o o tg τ α σ σ α α =− = − o ∴ = += max 2 2 min 2 2 1 2 3 ( ) 2 2 50 50 57.0 ( ) ( 20) 2 2 7.0 57.0 0 7.0 xy xy xy MPa MPa MPa MPa σ σσ σσ τ σ σ σσ ⎧ + − ⎨ =± + ⎩ ⎧ = ± +− = ⎨ ⎩− ∴ = = =− (2) 画主平面位置及主应力方向： σx>σy，α0面对应σmax。 19.3o σ3 σ1 (3) 最大剪应力 1 3 max 57.0 7.0 32.0 2 2 MPa σ σ τ − + == = (4) 应力圆 (50,-20) (0, 20) 38.6o -7.0 57.0 σ τ

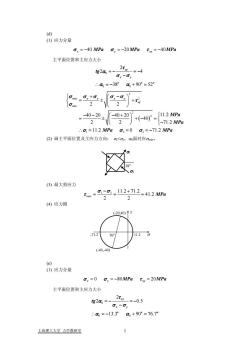
(d) (1)应力分量O,=-40 MPa ,=-20MPa y=-40MPa主平面位置和主应力大小27gtg2αg=a,-0,α + 90°= 52'.α,=-38°o,+o,amax0+tgmin2) +(-40)°- 1.2 MPa-40+20）-20{-71.2 MPa2.. 0, =11.2 MPa0, =-71.2 MPa0=U(2）画主平面位置及主应力方向：α<0y，αo面对应omin(3)最大剪应力_11.2+71.2=41.2MPa(4)应力圆(e)(1)应力分量,=0,=-80MPa T,=20MPa主平面位置和主应力大小27tg2αg-0.5a,-a,.. α = -13.3°α + 90°= 76.7°上海理工大学力学教研室

(d) (1) 应力分量 40 20 40 σ x yx = − MPa σ τ = − MPa y = − MPa 主平面位置和主应力大小 0 0 0 2 2 4 38 90 52 xy x y o o tg τ α σ σ α α =− =− − o ∴ =− + = ( ) 2 max 2 min 2 2 1 2 3 2 2 40 20 40 20 11.2 40 2 2 71.2 11.2 0 71.2 xy xy xy MPa MPa MPa MPa σ σσ σσ τ σ σ σσ ⎧ + − ⎛ ⎞ ⎨ =± + ⎜ ⎟ ⎩ ⎝ ⎠ −− −+ ⎛ ⎞ ⎧ = ± +− = ⎜ ⎟ ⎨ ⎝ ⎠ ⎩− ∴ = = =− (2) 画主平面位置及主应力方向： σx<σy，α0面对应σmin。 38o σ3 σ1 (3) 最大剪应力 1 3 max 11.2 71.2 41.2 2 2 MPa σ σ τ − + == = (4) 应力圆 (-40,-40) (-20,40) 76o -71.2 11.2 σ τ (e) (1) 应力分量 0 80 20 σ x y = =− = σ τ MPa MPa xy 主平面位置和主应力大小 0 0 0 2 2 0. 13.3 90 76.7 xy x y o o tg 5 o τ α σ σ α α =− =− − ∴ =− + = 上海理工大学 力学教研室 1

max_o,+,+gr-a,y+tT.-+2-17m{-84.7MPa..a,=4.7MPa 0,=0g,=-84.7MPa(2）画主平面位置及主应力方向：a>0，αo面对应omax。/o(3)最大剪应力4.7+84.7=44.7MPa(4)应力圆(f)(1）应力分量,=30MPa t,=20MPao,=-20MPa主平面位置和主应力大小2g=0.8tg2αg=O,-0,.α%=19.3°α +90°=109.3°fomax_a, +o,.o.-o,y+tgmin[37MPa20+30-20 - 30 +20° ={-27MPa2..0, = 37MPa,=0 ,=-27MPa(2）画主平面位置及主应力方向：oKc，o0面对应0mmn。上海理工大学力学教研室

max 2 2 min 2 2 1 23 ( ) 2 2 80 80 4.7 ( ) 20 2 2 84.7 4.7 0 84.7 xy xy xy MPa MPa MPa MPa σ σσ σσ τ σ σ σσ ⎧ + − ⎨ =± + ⎩ − ⎧ = ± += ⎨ ⎩− ∴ = = =− (2) 画主平面位置及主应力方向： σx>σy，α0面对应σmax。 13.3o σ3 σ1 (3) 最大剪应力 1 3 max 4.7 84.7 44.7 2 2 MPa σ σ τ − + == = (4) 应力圆 (0,20) (-80,-20) 26.6o -84.7 4.7 σ τ (f) (1) 应力分量 20 30 20 σ x yx = − MPa MPa MPa σ τ = y = 主平面位置和主应力大小 0 0 0 2 2 0.8 19.3 90 109.3 xy x y o o tg o τ α σ σ α α =− = − ∴= + = max 2 2 min 2 2 1 23 ( ) 2 2 20 30 20 30 37 ( ) 20 2 2 27 37 0 27 xy xy xy MPa MPa MPa MPa σ σσ σσ τ σ σ σσ ⎧ + − ⎨ =± + ⎩ −+ −− ⎧ = ± += ⎨ ⎩− ∴ = = =− (2) 画主平面位置及主应力方向：σx<σy，α0面对应σmin。 上海理工大学 力学教研室 2

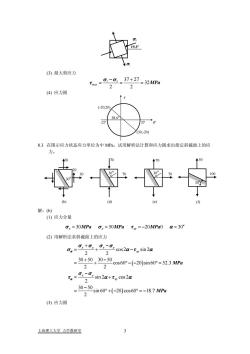
(3）最大剪应力37+2732MPa(4) 应力圆208.3.在图示应力状态应力单位为中MPa，试用解析法计算和应力圆求出指定斜截面上的应力0(d)(e)(f)解：(b)(1)应力分量o,=30MPa,=50MPaTm=-20MPa0α=30°(2)用解析法求斜截面上的应力+cos2α-ty sin2a. =30+50,3050cos60°-(-20)sin 60°= 52.3 MPa-0Isin2α+Tg cos2α30-50sin 60°+(-20)cos60°= -18.7 MPa(3)应力圆上海理工大学力学教研室

19.3o σ3 σ1 (3) 最大剪应力 1 3 max 37 27 32 2 2 MPa σ σ τ − + === (4) 应力圆 (30,-20) (-20,20) 38.6o -27 37 σ τ 8.3. 在图示应力状态应力单位为中 MPa，试用解析法计算和应力圆求出指定斜截面上的应 力。 70 70 (d) 30o 50 100 (f) 30o 70 70 (e) 30o 30 50 (b) 30o 20 解：(b) (1) 应力分量 30 50 20 0 30o σστ α x yx === MPa MPa y − MPa = (2) 用解析法求斜截面上的应力 ( ) ( ) cos 2 sin 2 2 2 30 50 30 50 cos 60 20 sin 60 52.3 2 2 sin 2 cos 2 2 30 50 sin 60 20 cos60 18.7 2 xy xy xy x y xy MPa MPa α α σ σ σσ σ α τ α σ σ τ α τ α + − =+ − + − = + °− − °= − = + − = ° + − ° = − (3) 应力圆 上海理工大学 力学教研室 3

30.-20(d)(1）应力分量0,=70MPa ,=-70MPag=0α=30°(2）用解析法求斜截面上的应力o2a-ysin2a7000+70cos60=35MPa-arsin2α+cos2a70 + 70sin 60°= 60.6MPa(3)应力圆(e)(1)应力分量,=70MPa,=70MPaT,=0α=30°(2）用解析法求斜截面上的应力o, +o,o-0-cos2a -t , sin 2a6._70 +70=70MPa0-0sin 2a +t , cos2a = 0（3）应力圆：为一点圆（70,0）上海理工大学力学教研室

60o σ τ (30,-20) (50, 20) (52.3, -18.7) (d) (1) 应力分量 70 70 0 30o σ σ τα xy x = = MPa − = MPa y = (2) 用解析法求斜截面上的应力 cos 2 sin 2 2 2 70 70 70 70 cos60 35 2 2 sin 2 cos2 2 70 70 sin 60 60.6 2 xy xy xy x y xy MPa MPa α α σ σ σσ σ ατ α σ σ τ α τ α + − =+ − − + = + °= − = + + = ° = (3) 应力圆 -70 70 (35,60.6) 60o σ τ (e) (1) 应力分量 o σ x = MPa σ y = MPa xy = ατ = 30 0 70 70 (2) 用解析法求斜截面上的应力 02cos2sin 2 70 2 7070 2sin2cos 22 + = − = = + = − − + + = ατα σσ τ ατα σσσσ σ α α x yx x yxyx MPa (3) 应力圆：为一点圆 (70,0) σ τ 上海理工大学 力学教研室 4

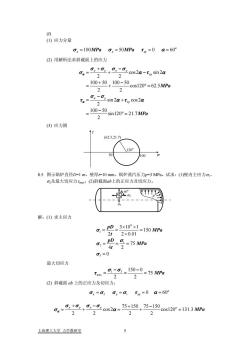
(f) (1)应力分量,=100MPa,=50MPa,=0α=60°(2）用解析法求斜截面上的应力,-++cos2a-tg sin2a100+50,100500s120°=62.5MPaOsin2α +fg cos2α100-50120°=21.7MPa(3)应力圆8.5：图示锅炉直径D=1m，壁厚=10mm，锅炉蒸汽压力p=3MPa。试求：(1)壁内主应力o1、及最大切应力tmax；（2)斜截面ab上的正应力及切应力TTTTL解：(1)求主应力o =PD_ 3×10°×1=150 MPa2t=2x0.01DD-%=75 MPag, =4t20,=0最大切应力-93-150-075 MPa2(2）斜截面ab上的正应力及切应力：=0α=60°0,=0,a,=a_75+150,75-150a,+0,+o,-0,ga--cos2αcos120° =131.3 MPa222上海理工大学力学教研室5

(f) (1) 应力分量 100 50 0 60o σ στ x yx = == MPa MPa y α = (2) 用解析法求斜截面上的应力 cos2 sin 2 2 2 100 50 100 50 cos120 62.5 2 2 sin 2 cos 2 2 100 50 sin120 21.7 2 xy xy xy x y xy MPa MPa α α σ σ σσ σ ατ α σ σ τ α τ α + − =+ − + − = + °= − = + − = ° = (3) 应力圆 50 100 (62.5,21.7) 120o σ τ 8.5. 图示锅炉直径D=1 m，壁厚t=10 mm，锅炉蒸汽压力p=3 MPa。试求：(1)壁内主应力σ1、 σ2及最大切应力τmax；(2)斜截面ab上的正应力及切应力。 p σ1 σ2 60o 解：(1) 求主应力 6 1 1 2 3 3 10 1 150 2 2 0.01 75 4 2 0 pD MPa t pD MPa t σ σ σ σ × × == = × = == = 最大切应力 1 3 max 150 0 75 2 2 MPa σ σ τ − − === (2) 斜截面 ab 上的正应力及切应力： 2 1 0 60o σσ σσ τ α x yx = = == y 75 150 75 150 cos 2 cos120 131.3 22 22 xy xy o MPa α σ σ σσ σ α + − + − =+ = + = 上海理工大学 力学教研室 5

sin20sin120°=-32.5MPa8.6.图示矩形截面梁某截面上的弯矩和剪力分别为M=10kN.m，Q=120kN。试绘出截面上1、2、3、4各点的应力状态单元体，并求其主应力。解：（1）截面上1点的应力：M10×1030a) ==-120MPa T=0abirx0.05x0.p应力状态单元：主应力：-120MPag,=0=0(2）截面上2点的应力：3g3.120×103= 36 MPa0(2) =0 (2) =2*0.05x0.12bh应力状态单元：主应力： = 36 MPa0,=-36 MPaT(3）截面上3点的应力：--= 60 MPa0T(3)0.05x0.05×0.mbl,12应力状态单元：上海理工大学力学教研室

75 150 sin 2 sin120 32.5 2 2 x y o MPa α σ σ τ α − − == = − 8.6. 图示矩形截面梁某截面上的弯矩和剪力分别为 M=10 kN.m，Q=120 kN。试绘出截面上 1、 2、3、4 各点的应力状态单元体，并求其主应力。 25 50 100 Q 50 M 1 2 3 4 x z y 解：(1) 截面上 1 点的应力： 3 (1) (1) 2 2 10 10 120 0 1 1 0.05 0.1 6 6 M MPa bh σ τ × =− =− = − = × × 应力状态单元： 120MPa 主应力： 12 3 σ =σ σ = =− 0 120 MPa (2) 截面上 2 点的应力： 3 (2) (2) 3 3 120 10 0 36 2 2 0.05 0.1 Q MPa bh σ τ × = =− =− × = × 应力状态单元： 36MPa 主应力： 1 23 σ = == 36 0 36 MPa σ σ − MPa (3) 截面上 3 点的应力： ( ) (1) (3) * 3 60 2 120 10 0.025 0.05 0.0375 27 z MPa QS MPa (3) 3 0.05 0.1 0.05 12 z bI σ σ τ =− = ×× × × = = = × × 应力状态单元： 上海理工大学 力学教研室 6

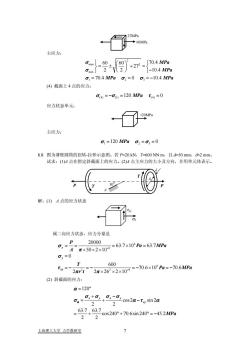
主应力：[0) +27 = [70.4 MPamax/=60±-10.4 MPagminV2,=0,=-10.4MPaα, = 70.4 MPa(4）截面上4点的应力：-α( =120 MPa T(4)=0(4)应力状态单元：20MP主应力：o,=120 MPa ,=0,=08.8.图为薄壁圆筒的扭转-拉伸示意图。若P=20kN，T-600NN-m，且d=50mm，-2mm试求：(1)4点在指定斜截面上的应力。(2)4点主应力的大小及方向，并用单元体表示。ta解：(）A点的应力状态属二向应力状态，应力分量是20000=63.7x10°Pa=63.7MPaaxA元×50×2×109,=0600tg=-2元r"-70.6×10°Pa=-70.6MPa2元×26*×2×10-9(2)斜截面的应力：α=120°o,+o,+grUaacos2α-tsin2a63.7, 63.7cos240°+ 70.6sin240°=-45.2MPa上海理工大学力学教研室

27MPa 60MPa 主应力： 2 max 2 min 1 2 3 60 60 70.4 27 2 2 10.4 70.4 0 10.4 MPa MPa MPa MPa σ σ σ σσ ⎫ ⎛ ⎞ ⎧ ⎬ ⎨ =± + = ⎜ ⎟ ⎭ ⎝ ⎠ ⎩− = == − (4) 截面上 4 点的应力： (4) (1) (4) σ = −= = σ τ 120 0 MPa 应力状态单元： 120MPa 主应力： 1 2 120 0 MPa σ = σ σ= =3 8.8. 图为薄壁圆筒的扭转-拉伸示意图。若 P=20 kN，T=600 NN·m，且 d=50 mm，δ=2 mm。 试求：(1)A 点在指定斜截面上的应力。(2)A 点主应力的大小及方向，并用单元体表示。 30o P T d δ A T P 解：(1) A 点的应力状态 σx τxy 属二向应力状态，应力分量是 6 6 6 2 29 20000 63.7 10 63.7 50 2 10 0 600 70.6 10 70.6 2 2 26 2 10 x y xy P Pa MPa A T Pa MPa r t σ π σ τ π π − − = = = × = × ×× = =− =− =− × =− × ×× (2) 斜截面的应力： 120 cos 2 sin 2 2 2 63.7 63.7 cos 240 70.6sin 240 45.2 2 2 o xy xy xy MPa α α σσ σσ σ α τ α = + − =+ − = + °+ °=− 上海理工大学 力学教研室 7

sin2α+cos2asin2470.6os24(3)主方向 2×(-70.6) = 2.222ttg2αg =a.-a,63.7α +90°=122.9°α%=32.9°(4)主应力a_g,+o,%y+om{109.3MPa3.7y +(-70.6)* =63.7V2{-45.6MPa2:.0,=109.3MPa 0,=0 ,=-45.6MPa（5）主单元体：0>0，00面对8.9.图示简支梁为36a工字染，P=140kN，1=4m。A点所在截面在P的左侧，且无限接近于P试求：(1)通过A点在与水平线成30°的斜面上的应力；(2)4点的主应力及主平面位置。IpA解：(1)4截面上的剪力和弯矩Q--140-70KN M--140×4=-140 Nm(2)A点的应力状态(3）截面几何性质上海理工大学力学教研室

sin 2 cos 2 2 63.7 sin 240 70.6cos 240 7.7 2 x y xy MPa α σ σ τ α τ α − = + = °− °= (3) 主方向 0 0 0 2 2 ( 70.6) 2 2 63.7 32.9 90 122.9 xy x y o oo tg .22 τ α σ σ α α × − =− =− = − = += (4) 主应力 6.45 0 3.109 6.45 3.109 )6.70() 2 7.63 ( 2 7.63 ) 2 ( 2 1 2 3 2 2 22 min max MPa MPa MPa MPa xy yx yx =∴ −== ⎩ ⎨ ⎧ − ±= =−+ + − ± + = ⎩ ⎨ ⎧ σ σσ τ σσσσ σ σ (5) 主单元体：σx>σy，α0面对应σmax。 32.9o σ1 σ3 8.9. 图示简支梁为 36a工字梁，P=140 kN，l=4 m。A点所在截面在P的左侧，且无限接近于P。 试求：(1)通过A点在与水平线成 30o 的斜面上的应力；(2)A点的主应力及主平面位置。 解：(1) A 截面上的剪力和弯矩 h P A P P 140 l 140 4 70 140 2 2 4 4 Q kN M kNm × == = = = = (2) A 点的应力状态 (3) 截面几何性质 l/2 l/2 h/4 30o σx τxy 上海理工大学 力学教研室 8

1,=15800cmW =875cm3h=360mmB=136mmb=10mmt=15.8mm（4）应力分量140×10x0.36Mxh4=79.75MPaa.=15800×10g.=0[r-(-2]+[-2-倍]u"T870×103(0136[0.36′ (0.362×0.0158)15800×10-×0.018+ 0.01[(0.36-2×0.0158)_ 0.36*]2164=20.56MPa（5）斜截面上的应力α= 60°r+a,0ycos2α-tsin2αge79.7579.75xcos120°-20.56×sin120°=2.13MPa+sin2α+#gcos2αsin20 +20.56cos=24.25MPa（6）主方向2t2×20.56:0.516tg2α, :"o,-0,79.75α% +90° = 76.4α% = -13.6°（7）主应力fomx_o,+o,oy+tla.[84.7MPa79.75 ±79.75) +(20.56) =-5.0MPa..o, =84.7MPag,=-5.0MPaT三上海理工大学力学教研室

3 4 875 15800 360 136 10 15.8 W cm I cm z h mm B mm b mm t mm = = = = == （4）应力分量 ( ) ( ) ( ) ( ) 3 8 2 2 2 2 3 2 2 8 2 2 0.36 140 10 4 4 79.75 15800 10 0 2 2 8 2 4 16 70 10 0.136 { 0.36 0.36 2 0.0158 15800 10 0.01 8 0.01 0.36 2 0.0158 0.36 } 24 16 20.56 x z y xy z h M MPa I Q B b h h t h ht I b MPa σ σ τ − − × ×× == = × = ⎪ ⎪ ⎧ ⎫ ⎡ ⎤ − = −− + − ⎡ ⎤ ⎨ ⎬ ⎢ ⎥ ⎣ ⎦ ⎪ ⎪ ⎢ ⎥ ⎩ ⎭ ⎣ ⎦ × = − ⎡ − × ⎤ × × ⎣ ⎦ ⎡ ⎤ − × + − ⎢ ⎥ ⎣ ⎦ = （5）斜截面上的应力 60 cos 2 sin 2 2 2 79.75 79.75 cos120 20.56 sin120 2 2 2.13 sin 2 cos 2 2 79.75 sin120 20.56 cos120 2 24.25 o xy xy xy o o x y xy o o MPa MPa α α α σσ σσ σ α τ σ σ τ α τ α = + − =+ − = + × −× = − = + = × +× = α （6）主方向 0 0 0 2 2 20.56 2 0.516 79.75 13.6 90 76.4 xy x y o oo tg τ α σ σ α α × =− =− =− − =− + = （7）主应力 max 2 2 min 2 2 1 2 3 ( ) 2 2 79.75 79.75 84.7 ( ) (20.56) 2 2 5.0 84.7 0 5.0 xy xy xy MPa MPa MPa MPa σ σσ σσ τ σ σ σσ ⎧ + − ⎨ =± + ⎩ ⎧ =± + = ⎨ ⎩− ∴ = = =− 上海理工大学 力学教研室 9