内蒙古科技大学：《材料力学》课程教学资源（习题解答）弯曲变形

7.2.用积分法求图示各梁的挠曲线方程、自由端的截面转角，跨度中点的挠度和最大挠度。设EI=常量解： (b)(1）列弯矩方程[M(x)=-PxX, E[0,a][M(s)=-Px, -P(x, -a) x E[a,2a)(2）曲线近似微分方程[EIv} = M,(x) = -Px,[EIv, = M,(x2) =-Px, - P(x -0)(3）直接积分两次Elv =+C(x -a)° +C,Elv,EIy:-x +Cx, + D,(x, -a) +C,x, +D,Elv,(4)确定积分常数边界条件：x=2a: V=0, =0光滑连续条件：X=x,=a? =v2, =v求解得积分常数a" D,=D,=-PaC,=C,=号Pa梁的挑曲线方程和转角方程是

7.2. 用积分法求图示各梁的挠曲线方程、自由端的截面转角，跨度中点的挠度和最大挠度。 设 EI=常量。 P a a P A B C (b) q l/2 l/2 A B C (c) 解：(b) (1) 列弯矩方程 P P A B x1 C x2 11 1 1 22 2 2 2 ( ) [0, ] ( ) ( ) [ ,2 ) M x Px x a M x Px P x a x a a ⎧ =− ∈ ⎨ ⎩ =− − − ∈ (2) 挠曲线近似微分方程 " 1 11 1 " 2 22 2 2 ( ) () ( ) EIv M x Px EIv M x Px P x a ⎧⎪ = =− ⎨ ⎪⎩ = =− − − (3) 直接积分两次 ' 2 1 11 '2 2 2 22 2 ( ) 2 2 P EIv x C P P E 2 Iv x x a C ⎧ =− + ⎪⎪ ⎨ ⎪ =− − − + ⎪⎩ 3 1 1 11 1 3 3 2 2 2 22 6 ( ) 6 6 P EIv x C x D P P E 2 Iv x x a C x D ⎧ =− + + ⎪⎪ ⎨ ⎪ =− − − + + ⎪⎩ (4) 确定积分常数 边界条件： ' 2 22 x av v = 2 : 0, 0 = = 光滑连续条件： ' ' 1 2 12 12 xxa vv vv = = == : , 求解得积分常数 3 21 2 21 2 7 2 5 == −== PaDDPaCC 梁的挠曲线方程和转角方程是

[Ei=-x+pa?Ev,--x-(,-a)+Pa[Ey =-x+Pax--Pa[En---a-) pix-p(5）自由端的转角、跨度中点的揽度和最大挠度x=0:Jns=) =-7Pd,0,=m=SPa2EI2EI令x=a:-注：挠度方向向下，转角为逆时针转向。c)(1）求约束反力并列出弯矩方程“AR-- M-M(x)=-3+号xe(0)[M(a)-- eg,(2）挠曲线近似微分方程[E = M(a)--3++x[Eng =M(s)=-(--)(3）直接积分两次上海理工大学力学教研室

' 22 1 1 '2 2 2 22 5 2 2 5 ( ) 22 2 P EIv x Pa P P 2 EIv x x a Pa ⎧ =− + ⎪⎪ ⎨ ⎪ =− − − + ⎪⎩ 32 3 11 1 3 32 2 22 2 5 7 62 2 5 7 ( ) 66 2 2 P EIv x Pa x Pa P P 3 EIv x x a Pa x Pa ⎧ =− + − ⎪⎪ ⎨ ⎪ =− − − + − ⎪⎩ (5) 自由端的转角、跨度中点的挠度和最大挠度 令x1=0： 3 2 ' max 1 1 7 5 , 2 2 A Pa P f v v a EI E = =− = = θ I 令x1=a： 3 1 7 6 C Pa f v EI = =− 注：挠度方向向下，转角为逆时针转向。 (c) (1) 求约束反力并列出弯矩方程 x1 x2 q A B C RA MA 2 3 2 8 A A ql ql R M = = ( ) 2 1 1 1 1 2 2 2 2 2 3 ( ) (0, ] 82 2 ( ) [ , ] 2 2 ql ql l M x x x ql x l M x x l ⎧ ⎪ =− + ∈ ⎪ ⎨ ⎪ − = − ∈ ⎪⎩ (2) 挠曲线近似微分方程 ( ) 2 " 1 11 2 " 2 2 22 3 ( ) 8 2 ( ) 2 ql ql E 1 Iv M x x ql x EIv M x ⎧ = =− + ⎪ ⎪ ⎨ ⎪ − = =− ⎪⎩ (3) 直接积分两次 上海理工大学 力学教研室 1

[EW=-x+x+,[Eng = (l-x)+C[EW=--x++Cx+D[Em-+ + 24(4）确定积分常数边界条件：x=0: =0, =0光滑连续条件：X=x, =1=v2, =y求解得积分常数D, = 15glG=D,=0 C,=-7q38448梁的挠曲线方程和转角方程是[Em =--3 x+x[Em - (-- 7[Em--x+2448(5）自由端的转角、跨度中点的挠度和最大挠度令x;=l:41q0,=y;=- 7glJmax = V, =-384EI48EI令x=1/2:7ql4fc=y :192EI7.4.求图示等截面悬臂梁的挠曲线方程，自由端的挠度和转角。求解时应注意到梁在CB段内无载荷，故CB仍为直线。上海理工大学力学教研室

( ) 2 ' 2 1 11 3 ' 2 2 2 3 8 4 6 ql ql E 1 Iv x x C ql x EIv C ⎧ = − ++ ⎪ ⎪ ⎨ ⎪ − = + ⎪⎩ ( ) 2 2 3 1 1 11 1 4 2 2 2 2 3 16 12 24 ql ql 1 2 EIv x x C x D ql x EIv C x D ⎧ = − + ++ ⎪ ⎪ ⎨ ⎪ − =− + + ⎪⎩ (4) 确定积分常数 边界条件： ' 1 11 x vv = 0: 0, 0 = = 光滑连续条件： ' ' 1 2 12 1 : , 2 l xx vv vv = = = = 2 求解得积分常数 3 4 11 2 2 7 1 0 48 384 ql ql CD C D = = =− = 5 梁的挠曲线方程和转角方程是 ( ) 2 ' 2 1 1 3 3 ' 2 2 3 8 4 7 6 4 ql ql 1 8 EIv x x ql x ql EIv ⎧ =− + ⎪ ⎪ ⎨ ⎪ − = − ⎪⎩ ( ) 2 2 3 1 11 4 3 4 2 2 2 3 16 12 7 15 24 48 384 ql ql EIv x x ql x ql ql EIv x ⎧ =− + ⎪ ⎪ ⎨ ⎪ − =− − + ⎪⎩ (5) 自由端的转角、跨度中点的挠度和最大挠度 令x1=l： 4 3 ' max 2 2 41 7 , 384 48 B ql ql f v v EI E = =− = =− θ I 令x1=l/2： 4 1 7 192 C ql f v EI = =− 7.4. 求图示等截面悬臂梁的挠曲线方程，自由端的挠度和转角。求解时应注意到梁在 CB 段 内无载荷，故 CB 仍为直线。 上海理工大学 力学教研室 2

P解：（1）求约束反力R,=PMA= Pa(2）列AC段的弯矩方程M(x)=Px- Paxe(0,a)(3）曲线近似微分方程EIv"= M(x)= Px - Pa(4）直接积分两次EIv- Pax +CEly*?+Cx+D(5）确定积分常数边界条件：x=0: v=v=0得积分常数：C=D=0(6)AC段的挠曲线方程和转角方程Elv'-PaxEIV()C截面的挠度和转角令x-a:Pa?Pa30.fc=-2EI3EI(8）自由端的挠度和转角梁的变形：上海理工大学力学教研室n

a l P (a) 解：(1) 求约束反力 A B C P MA RPMP A A = = a (2) 列 AC 段的弯矩方程 M x Px Pa x a ( ) (0, ] = − ∈ (3) 挠曲线近似微分方程 EIv M x Px Pa '' ( ) = = − (4) 直接积分两次 2 3 2 ' 2 6 2 P EIv x Pax C P Pa EIv x x Cx D = −+ = − ++ (5) 确定积分常数 边界条件： x vv = 0: ' 0 = = 得积分常数： C D= = 0 (6) AC 段的挠曲线方程和转角方程 2 3 2 ' 2 6 2 P EIv x Pax P Pa EIv x x = − = − (7) C 截面的挠度和转角 令 x=a： 2 3 2 3 C C Pa P f a EI E θ =− =− I (8) 自由端的挠度和转角 梁的变形： RA x 上海理工大学 力学教研室 3

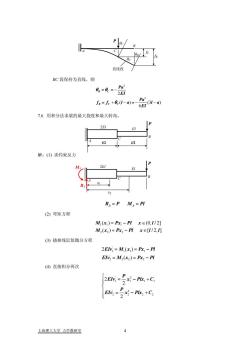
目线用BC段保持为直线，则0. - -_Pa(31 -a)Je= fe +0c(I-a)=-7.6.用积分法求梁的最大挠度和最大转角。解：（1）求约束反力R,=P M=Pl(2)弯矩方程M(x)= Px, - PIxe (0,1/2)M,(x,)=Px, -Pl xE[1/2,1](3）挠曲线近似微分方程2EIv = M,(x)= Px - PIElvz = M2(x2)= Px2 - PI(4）直接积分两次x - Plx; +C,EIv, =-Plx,+Cy上海理工大学力学教研室

BC 段保持为直线，则 2 2 2 ( ) (3 6 B C B CC Pa EI Pa f f la la EI θ θ θ = = − = + − =− − ) l 7.6. 用积分法求梁的最大挠度和最大转角。 l/2 P A B C l/2 EI 2EI P A B C fC θC θC θB fB 直线段 解：(1) 求约束反力 x2 RPMP A A = = (2) 弯矩方程 11 1 22 2 ( ) (0, / 2] ( ) [ / 2, ] M x Px Pl x l M x Px Pl x l l = − ∈ =− ∈ (3) 挠曲线近似微分方程 ' 1 11 1 ' 2 22 2 2 () ( ) EIv M x Px Pl EIv M x Px Pl = = − = =− (4) 直接积分两次 ' 2 111 ' 2 2 22 2 2 2 P 1 2 EIv x Plx C P EIv x Plx C ⎧ = − + ⎪⎪ ⎨ ⎪ = −+ ⎪⎩ RA MA x1 P A B C EI 2EI 上海理工大学 力学教研室 4

[2Em=x-号x+C++D,[En-Sr-++C++D.(5）确定积分常数边界条件：x=0: =0, =0光滑连续条件：X=x,=1/2: M=V2, V=v2求解得积分常数C,=0 C,=_prpD,=0 D,=-2pri16梁的挠曲线方程和转角方程是[2EIV=Px-PIx--x-Pls+torrElv, =[2EM=号x-号x[Em-x-号x+-m-1(6）最大挑度和最大转角发生在自由端令x2=1:_3Pr35PI?Jmax =0max = -16EI16EI7.7.用叠加法求图示各梁截面A的挠度和截面B的转角。EI=常量。图α和d可利用题6-4中得到的结果。Mo-PLT★(d)解: (a)(1)P单独作用时上海理工大学力学教研室

3 2 1 1 11 3 2 2 2 22 2 6 2 6 2 P Pl 1 2 EIv x x C x D P Pl EIv x x C x D ⎧ = − ++ ⎪⎪ ⎨ ⎪ = − ++ ⎪⎩ (5) 确定积分常数 边界条件： ' 1 11 x vv = 0: 0, 0 = = 光滑连续条件： ' ' 1 2 12 12 xxl vv vv == = = /2: , 求解得积分常数 2 3 1 2 12 3 1 0 0 16 24 C C Pl D D Pl = = = =− 梁的挠曲线方程和转角方程是 ' 2 111 ' 2 2 22 2 2 3 2 1 P EIv x Plx P 2 6 EIv x Plx Pl ⎧ = − ⎪⎪ ⎨ ⎪ = −+ ⎪⎩ 3 2 11 1 32 2 22 2 2 2 6 2 3 1 6 2 16 24 P Pl EIv x x P Pl 3 EIv x x Pl x Pl ⎧ = − ⎪⎪ ⎨ ⎪ =− + − ⎪⎩ (6) 最大挠度和最大转角发生在自由端 令x2=l： 3 2 max max 3 5 , 16 16 Pl Pl f EI E = − θ = − I 7.7. 用叠加法求图示各梁截面 A 的挠度和截面 B 的转角。EI=常量。图 a 和 d 可利用题 6-4 中得到的结果。 P l/2 l/2 M0=PL A B (a) A B q 2l/3 l/3 (d) P=ql 解：(a) (1) P 单独作用时 上海理工大学 力学教研室 5

DIPI324EIBEIPI?P2)B8EI2EI(2）Mo单独作用时)pt0A2EI8EI_ PL-1__ PI?98FIEI(3）P和Mo共同作用时AJ= Jap + Jam, =-6EI9Pl?0g=0B)p+0BMo8EI(b)P=q+21/3(1)P单独作用时((()福-() -- 4012fAP=6EIL4OF“5ql3eB)p=81EI6EIl(2）q单独作用时()(2(2））汽11gl[3-2JA)g =-+（3)=-972EI24EI3Cn-e(3）P和q共同作用时上海理工大学力学教研室

3 3 ) 2 2 ) 2 3 24 2 2 8 A P B P l P Pl f EI E l P I Pl EI E θ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ =− =− ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ =− =− I (2) M0单独作用时 0 2 3 ) 2 ) 2 2 8 A Mo B M l Pl Pl f EI E Pl l Pl I EI EI θ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ =− =− ⋅ =− =− (3) P和M0共同作用时 0 0 3 ) ) 2 ) ) 6 9 8 A AP AM B BP BM Pl ff f EI Pl EI θθ θ = + =− = + =− (b) A B q 2l/3 l/3 P=ql (1) P 单独作用时 ( ) 2 2 4 2 ) 3 ) 2 3 3 2 4 6 3 3 243 2 2 33 3 5 6 81 A P B P l l ql l l ql f l EIl EI ll l ql l ql EIl EI θ ⎛ ⎞⎛ ⎞ ⎜ ⎟⎜ ⎟⎛ ⎞ ⎝ ⎠⎝ ⎠ ⎛ ⎞ ⎛⎞ = − ⎜ ⎟ − − =− ⎜ ⎟ ⎜⎟ ⎝ ⎠ ⎝⎠ ⎝ ⎠ ⎛ ⎞⎛ ⎞⎛ ⎞ ⎜ ⎟⎜ ⎟⎜ ⎟ + ⎝ ⎠⎝ ⎠⎝ ⎠ = = (2) q 单独作用时 2 3 4 3 ) 3 ) 2 3 2 2 11 2 24 3 3 972 24 A q B q l q ll q f ll l EI E ql I EI θ ⎛ ⎞ ⎜ ⎟⎛ ⎞ ⎝ ⎠ ⎛⎞⎛⎞ =− − + =− ⎜ ⎟ ⎜⎟⎜⎟ ⎝⎠⎝⎠ ⎝ ⎠ = (3) P 和 q 共同作用时 上海理工大学 力学教研室 6

4gt411qttqt4a= JA)p + fa)m -243EI972EI36EI5qqf67gl0,=0mp+0mM.B1EI24EI"648EI7.8.用叠加法求图示外伸梁外伸端的挠度和转角，设E=常量P=解：（1）分解成简单载荷作用[P=qa(2)分别求出简单载荷作用时外伸端的变形：转角0 0m 40 - 16EI=4EIe) =- g6EIqa2-2aqag() = d() = -3EI3EI挠度I 0m- -14EIqdJe(d) - SEIIno, e a=-3EI(3)叠加上海理工大学力学教研室7

0 0 4 4 ) ) 33 3 ) ) 4 11 243 972 36 5 67 81 24 648 A AP AM B BP BM ql ql ql ff f 4 EI EI ql ql ql EI EI EI EI θθ θ = + =− − =− =+ = = 7.8. 用叠加法求图示外伸梁外伸端的挠度和转角，设 EI=常量。 A B P=qa q a a a C D 解：(1) 分解成简单载荷作用 (1) A B P=qa a a a C D (2) qa 2 /2 qa A B q a a C D a (2) 分别求出简单载荷作用时外伸端的变形： 转角 2 3 (1) (1) 3 (2) 2 3 (3) (3) (2 ) 16 4 6 1 2 2 3 3 B D B B D qa a qa EI EI qa EI qa a qa EI E θ θ θ θ θ ⋅ == = = − ⋅ = =− =− I 挠度 4 (1) (1) 4 (2) 4 (3) (3) 4 8 3 B D B B D qa f a EI qa f EI qa f a EI θ θ = ⋅= = − = ⋅ =− (3) 叠加 (3) A B a a a C D qa qa 2 /2 上海理工大学 力学教研室 7

0g= 00 +00) +00, -45qafe= foo + fea + feo =-24EI7.10.桥式起重机的最大载荷为P=20kN。起重机大梁为32a工字钢，E=210GPa，7-8.7m规定[)-1/500，试校核大梁刚度。ALP解：（1）当起重机位于梁中央时，梁变形最大：计算简图为★P1/2(2）梁的最大挠度发生在C截面(3）查表得（32a工字钢）I=11100cmq=52.717kg/m=516.6N/m(4）刚度计算20×10°×8.765×516.6×8.764[m/-4(21010 (10-10) 38(21010)(10 10)1=0.0175m0.01010.03梁的刚度足够。注：这里考虑工字梁的自重影响。7.12.直角析轴杆与ABC如图所示。A处为一轴承，允许AC轴的端截面在轴承内自由转动，但不能上下移动。已知P=60N，E=210GPa，G=0.4E。试求截面B的垂直位移。AP300//B上海理工大学力学教研室

3 (1) (2) (3) 4 (1) (2) (3) 4 5 24 BB B B BB B B qa EI qa ff f f EI θθ θ θ = + + =− = + + =− 7.10. 桥式起重机的最大载荷为 P=20 kN。起重机大梁为 32a 工字钢，E=210 GPa，l=8.7 m。 规定[f]=l/500，试校核大梁刚度。 l B P A 解：(1) 当起重机位于梁中央时，梁变形最大；计算简图为 l/2 B P A l/2 q C (2) 梁的最大挠度发生在 C 截面 3 4 max ( ) ( ) 5 48 384 C CP Cq Pl ql f ff f EI E == + = + I (3) 查表得（32a 工字钢） 4 I = == 11100 52.717 / 516.6 / cm q kg m N m (4) 刚度计算 ( )( ) ( )( ) 3 3 4 max 98 98 20 10 8.76 5 516.6 8.76 48 210 10 11100 10 384 210 10 11100 10 0.0120 0.00170 0.0137 [ ] 0.0175 500 f l m f m − − × × × × = + ×× ×× = + = == ≺ 梁的刚度足够。 注：这里考虑工字梁的自重影响。 7.12. 直角析轴杆与 ABC 如图所示。A 处为一轴承，允许 AC 轴的端截面在轴承内自由转动， 但不能上下移动。已知 P=60 N，E=210 GPa，G=0.4 E。试求截面 B 的垂直位移。 A B C 500 300 P 10 5 φ20 上海理工大学 力学教研室 8

解：（1）分析变形：AB发生弯曲变形，AC发生扭转变形；(2)计算A、C相对扭转角T.AC_P.AB.ACPAC =GI,Gl,由此引起B截面的垂直位移(向下)P.AB.AC32×60×0.3*×0.58B(1)=PAC-AB:2.05mm0.4×210×10×元×0.024G.rd32(3)计算AB变形引起B截面的位移(向下)PAB60 ×0.338 8(2) ==6.17mm3×210×10°×0.005×0.0F3EI12(4)计算B截面的总体位移(向下)8g =88() +8s(2) =8.22mm7.14.滚轮沿等截面简支梁移动时，要求滚轮恰好走一水平路径，试问须将图示梁的轴线预弯成怎样的曲线？解：（1）查表得水平简支梁受集中力作用时的挠曲线方程 Px(-[r--(1-x)]v(x)=6EIlPx(1-x)?3EIl(2)预弯的曲线方程Px (1-x)*y(x)=-(x)=3EIl7.15.图中两根梁由铰链相互联接，EI相同，且EI=常量。试求P力作用点D的位移。P解：（1）对两根梁受力分析上海理工大学力学教研室

解：(1) 分析变形：AB 发生弯曲变形，AC 发生扭转变形； (2) 计算 A、C 相对扭转角 AC p p T AC P AB AC GI GI ϕ ⋅ ⋅⋅ = = 由此引起 B 截面的垂直位移(向下) 2 2 (1) 4 9 4 32 60 0.3 0.5 2.05 0.4 210 10 0.02 32 B AC P AB AC AB mm d G δ ϕ π π ⋅ ⋅ ×× × =⋅= = = × × ×× ⋅ (3) 计算 AB 变形引起 B 截面的位移(向下) 3 3 (2) 3 9 60 0.3 6.17 3 0.005 0.01 3 210 10 12 B P AB mm EI δ × = = = × × ×× (4) 计算 B 截面的总体位移(向下) (1) (2) 8.22 δ BB B = δ δ + = mm 7.14. 滚轮沿等截面简支梁移动时，要求滚轮恰好走一水平路径，试问须将图示梁的轴线预 弯成怎样的曲线？ A B P l x y x 解：(1) 查表得水平简支梁受集中力作用时的挠曲线方程 ( ) ( ) ( ) 2 2 2 2 2 ( ) 6 3 Px l x v x l x l x EIl Px l x EIl − = − ⎡ − − − ⎤ ⎣ ⎦ − = − (2) 预弯的曲线方程 ( ) ( ) 2 2 ( ) 3 Px l x yx vx EIl − =− = 7.15. 图中两根梁由铰链相互联接，EI 相同，且 EI=常量。试求 P 力作用点 D 的位移。 A B P a a a C D a E 解：(1) 对两根梁受力分析 上海理工大学 力学教研室 9